高中数学人教B版 (2019)必修 第三册7.4 数学建模活动：周期现象的描述学案设计

这是一份高中数学人教B版 (2019)必修 第三册7.4 数学建模活动：周期现象的描述学案设计，共6页。学案主要包含了教学过程等内容，欢迎下载使用。

【教学过程】
一、情境导入
由图片及诗词引入钱塘江大潮，介绍钱塘江大潮是世界三大潮涌之一，通过小学课文《观潮》及视频感受钱塘江大潮的壮观。提出问题——如何描述潮汐变化，初步了解数学建模过程。
二、合作探究
例：海水受日月的引力，在一定的时候发生涨落的现象叫潮。一般地，早潮叫潮，晚潮叫汐。在通常情况下，船在涨潮时驶进航道，靠近码头；卸货后，在落潮时返回海洋。下表是某港口某天的时刻与水深关系的预报。
（1）选用一个函数来近似描述这一天该港口的水深与时间的关系，给出整点时水深的近似数值（精确0.001 m）。
（2）一条货船的吃水深度（船底与水面的距离）为4 m，安全条例规定至少要有1.5 m的安全间隙（船底与洋底的距离），该船这一天何时能进入港口？在港口能呆多久？
（3）某船的吃水深度为4 m，安全间隙为1.5 m，该船这一天在2：00开始卸货，吃水深度以0.3 m/h的速度减少，如果这条船停止卸货后需0.4 h才能驶到深水域，那么该船最好在什么时间停止卸货，将船驶向较深的水域？
解析：（1）以时间x（单位：h）为横坐标，水深y（单位：m）为纵坐标，在直角坐标系中画出散点图（图1）。根据图像，可以考虑用函数y＝A·sin（ωx＋φ）＋h刻画水深与时间之间的对应关系。从数据和图像可以得出：
A＝2．5，h＝5，T＝12．4，φ＝0；
由T＝eq \f(2π,ω)＝12．4，得ω＝eq \f(5π,31)。
所以，这个港口的水深与时间的关系可用函数y＝2．5sineq \f(5π,31)x＋5近似描述。
由上述关系式易得港口在整点时水深的近似值（表）：
（2）货船需要的安全水深为4＋1．5＝5．5m，所以当y≥5．5时就可以进港。令
2．5sineq \f(5π,31)x＋5＝5．5，sineq \f(5π,31)·x＝0.2．
由计算器可得
0.2013579208≈0.2014．
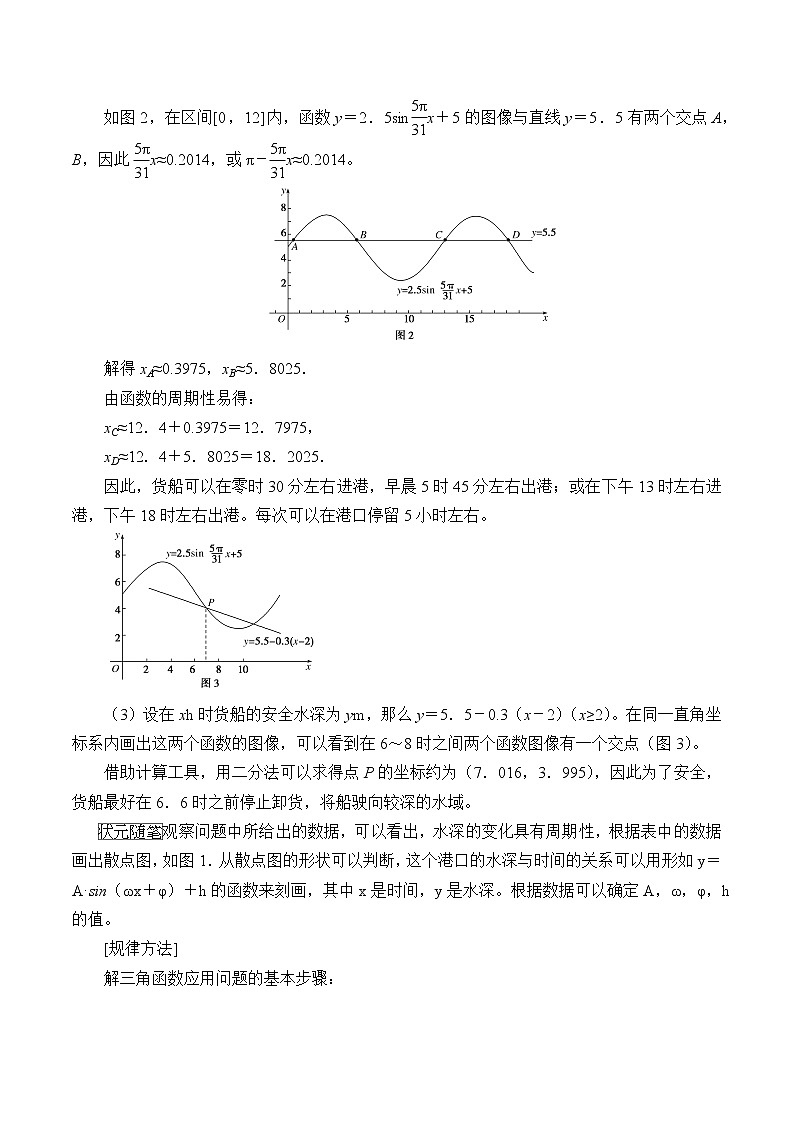
如图2，在区间[0，12]内，函数y＝2．5sineq \f(5π,31)x＋5的图像与直线y＝5．5有两个交点A，B，因此eq \f(5π,31)x≈0.2014，或π－eq \f(5π,31)x≈0.2014。
解得xA≈0.3975，xB≈5．8025．
由函数的周期性易得：
xC≈12．4＋0.3975＝12．7975，
xD≈12．4＋5．8025＝18．2025．
因此，货船可以在零时30分左右进港，早晨5时45分左右出港；或在下午13时左右进港，下午18时左右出港。每次可以在港口停留5小时左右。
（3）设在xh时货船的安全水深为ym，那么y＝5．5－0.3（x－2）（x≥2）。在同一直角坐标系内画出这两个函数的图像，可以看到在6～8时之间两个函数图像有一个交点（图3）。
借助计算工具，用二分法可以求得点P的坐标约为（7．016，3．995），因此为了安全，货船最好在6．6时之前停止卸货，将船驶向较深的水域。
eq \x(状元随笔)观察问题中所给出的数据，可以看出，水深的变化具有周期性，根据表中的数据画出散点图，如图1．从散点图的形状可以判断，这个港口的水深与时间的关系可以用形如y＝A·sin（ωx＋φ）＋h的函数来刻画，其中x是时间，y是水深。根据数据可以确定A，ω，φ，h的值。
[规律方法]
解三角函数应用问题的基本步骤：
提醒：关注实际意义求准定义域。
三、课堂小结
1．曲线y＝A·sin（ωx＋φ）的应用实质上是物理方面的知识。所以建立该类问题的数学模型一定要结合物理知识进行。
2．解答三角函数应用题的基本步骤可分为四步：审题、建模、解模、还原评价。
（1）构建三角函数模型解决具有周期变化现象的实际问题。
（2）对于测量中的问题归结到三角形中去处理，应用三角函数的概念和解三角形知识解决问题。
四、当堂达标
1．思考辨析
（1）函数y＝|sinx＋eq \f(1,2)|的周期为π。（ ）
（2）一个弹簧振子做简谐振动的周期为0.4s，振幅为5cm，则该振子在2s内通过的路程为50cm。（ ）
（3）电流强度I（A）随时间t（s）变化的关系式是I＝5sineq \b\lc\(\rc\)(\a\vs4\al\c1(100πt＋\f(π,3)))，则当t＝eq \f(1,200)s时，电流强度I为eq \f(5,2)A。（ ）
提示：（1）错误。函数y＝|sinx＋eq \f(1,2)|的周期为2π。
（2）错误。一个周期通过路程为20cm，所以2s内通过的路程为20×eq \f(2,0.4)＝100（cm）。
（3）正确。
答案：（1）×（2）×（3）√
2．在两个弹簧上各有一个质量分别为M1和M2的小球做上下自由振动。已知它们在时间t（s）离开平衡位置的位移s1（cm）和s2（cm）分别由s1＝5sineq \b\lc\(\rc\)(\a\vs4\al\c1(2t＋\f(π,6)))，s2＝10cs2t确定，则当t＝eq \f(2π,3) s时，s1与s2的大小关系是（ ）。
A．s1＞s2
B．s1＜s2
C．s1＝s2
D．不能确定
答案：C。
解析：当t＝eq \f(2π,3)时，s1＝5sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4π,3)＋\f(π,6)))＝5sineq \f(3π,2)＝－5，
当t＝eq \f(2π,3)时，s2＝10cseq \f(4π,3)＝10×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))＝－5，
故s1＝s2．
3．一根长lcm的线，一端固定，另一端悬挂一个小球，小球摆动时离开平衡位置的位移s（cm）与时间t（s）的函数关系式为s＝3cseq \b\lc\(\rc\)(\a\vs4\al\c1(\r(\f(g,l))t＋\f(π,3)))，其中g是重力加速度，当小球摆动的周期是1s时，线长l＝________cm。
答案：eq \f(g,4π2)。
解析：由已知得eq \f(2π,\r(\f(g,l)))＝1，所以eq \r(\f(g,l))＝2π，eq \f(g,l)＝4π2，l＝eq \f(g,4π2)。
4．如图所示，某动物种群数量1月1日低至700，7月1日高至900，其总量在此两值之间依正弦型曲线变化。
（1）求出种群数量y关于时间t的函数表达式；（其中t以年初以来的月为计量单位）
（2）估计当年3月1日动物种群数量。
解：（1）设种群数量y关于t的解析式为y＝A·sin（ωt＋φ）＋b（A＞0，ω＞0），
则eq \b\lc\{\rc\ (\a\vs4\al\c1(－A＋b＝700，,A＋b＝900，))
解得A＝100，b＝800.
又周期T＝2×（6－0）＝12，
∴ω＝eq \f(2π,T)＝eq \f(π,6)，∴y＝100sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)t＋φ))＋800.
又当t＝6时，y＝900，
∴900＝100sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)×6＋φ))＋800，
∴sin（π＋φ）＝1，∴sin φ＝－1，
∴取φ＝－eq \f(π,2)，
∴y＝100sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)t－\f(π,2)))＋800.
（2）当t＝2时，
y＝100sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)×2－\f(π,2)))＋800＝750，
即当年3月1日动物种群数量约是750。教学目标
核心素养
1．了解三角函数是描述周期变化现象的重要函数模型，并会用三角函数模型解决一些简单的实际问题。（重点）
2．实际问题抽象为三角函数模型。（难点）
1．通过建立三角模型解决实际问题，培养数学建模素养。
2．借助实际问题求解，提升数学运算素养。
时刻
水深/m
时刻
水深/m
时刻
水深/m
0：00
5.0
9：18
2.5
18：36
5.0
3：06
7.5
12：24
5.0
21：42
2.5
6：12
5.0
15：30
7.5
24：00
4.0
时刻
0：00
1：00
2：00
3：00
4：00
5：00
水深/m
5．000
6．213
7．122
7．497
7．245
6．428
时刻
12：00
13：00
14：00
15：00
16：00
17：00
水深/m
4．497
5．748
6．812
7．420
7．420
6．812
时刻
6：00
7：00
8：00
9：00
10：00
11：00
水深/m
5．253
4．014
3．023
2．529
2．656
3．372
时刻
18：00
19：00
20：00
21：00
22：00
23：00
水深/m
5．748
4．497
3．372
2．656
2．529
3．023