2020-2021学年四川省成都市高一（上）期末数学试卷人教新课标A版

这是一份2020-2021学年四川省成都市高一（上）期末数学试卷人教新课标A版，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 设全集U＝{1, 2, 3, 4, 5}，集合M＝{2, 3, 4}，N＝{3, 4}，则∁U(M∪N)＝（ ）
A.{2, 3, 4}B.{1, 2, 5}C.{3, 4}D.{1, 5}

2. 下列函数中，与函数y＝x相等的是（ ）
A.B.C.D.

3. 已知角α的顶点与直角坐标系的原点重合，始边与x轴的非负半轴重合，且．若角α的终边上有一点P(x, 3)，则x的值为（ ）
A.−4B.4C.−3D.3

4. 设函数则f（f(0)）的值为（ ）
A.2B.3C.e3−1D.e2−1

5. 已知扇形的圆心角为30∘，面积为3π，则扇形的半径为（ ）
A.B.3C.D.6

6. 函数f(x)＝lnx+2x−9的零点所在区间是（ ）
A.(1, 2)B.(2, 3)C.(3, 4)D.(4, 5)

7. 已知函数，则函数f(x)的递减区间是（ ）
A.
B.
C.
D.

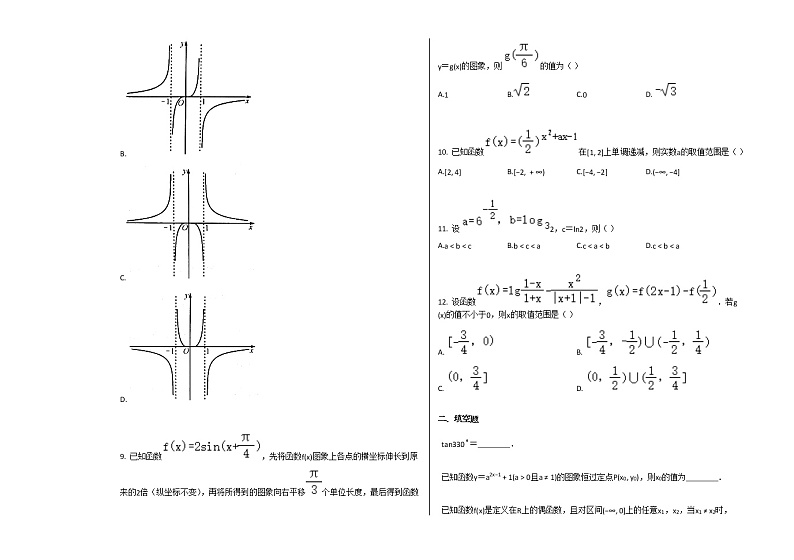
8. 函数f(x)＝的图象大致为（ ）
A.
B.
C.
D.

9. 已知函数，先将函数f(x)图象上各点的横坐标伸长到原来的2倍（纵坐标不变），再将所得到的图象向右平移个单位长度，最后得到函数y＝g(x)的图象，则的值为（ ）
A.1B.C.0D.

10. 已知函数在[1, 2]上单调递减，则实数a的取值范围是（ ）
A.[2, 4]B.[−2, +∞)C.[−4, −2]D.(−∞, −4]

11. 设2，c＝ln2，则（ ）
A.a
12. 设函数，．若g(x)的值不小于0，则x的取值范围是（ ）
A.B.
C.D.
二、填空题

tan330∘＝________．

已知函数y＝a2x−1+1(a>0且a≠1)的图象恒过定点P(x0, y0)，则x0的值为________．

已知函数f(x)是定义在R上的偶函数，且对区间(−∞, 0]上的任意x1，x2，当x1≠x2时，都有．若实数t满足f(2t+1)≤f(t−3)，则t的取值范围是________．

已知函数在上单调，且将函数f(x)的图象向右平移4π个单位长度后与原来的图象重合．当x∈(0, 4π)时，使得不等式成立的x的最大值为________．
三、解答题：

计算下列各式的值：
(Ⅰ)；
(Ⅱ)．

已知tanθ＝−2，且．
(Ⅰ)求sinθ，csθ的值；
(Ⅱ)求的值．

已知函数．
(Ⅰ)用函数单调性的定义证明函数f(x)在R上是增函数；
(Ⅱ)当x∈[1, 3]时，求函数g(x)＝lg3f(x)的最值．

1986年4月26日，一场地震造成乌克兰境内的切尔诺贝利核电站爆炸并引起大火．这一事故导致约8吨的强辐射物严重泄露，事故所在地被严重污染．主要辐射物是锶90，它每年的衰减率为2.47%，经专家模拟估计，辐射物中锶90的剩余量低于原有的8.46%时，事故所在地才能再次成为人类居住的安全区；要完全消除这次核事故对自然环境的影响至少需要800年．设辐射物中原有的锶90有a(0(Ⅰ)设经过t(t∈N*)年后辐射物中锶90的剩余量为P(t)吨，试求P(t)的表达式，并计算经过800年后辐射物中锶90的剩余量；
(Ⅱ)事故所在地至少经过多少年才能再次成为人类居住的安全区？（结果保留为整数）参考数据：ln0.0846＝−2.47，ln0.9753＝−0.03．

已知函数的最小值为−2，其图象经过点(0, −1)，且图象上相邻的最高点与最低点的横坐标之差的绝对值为．
(Ⅰ)求函数f(x)的解析式；
(Ⅱ)若关于x的方程f(x)−k＝0在上有且仅有两个实数根x1，x2，求实数k的取值范围，并求出x1+x2的值．

已知函数的定义域为R，其中a为实数．
(Ⅰ)求a的取值范围；
(Ⅱ)当a＝1时，是否存在实数m满足对任意x1∈[−1, 1]，都存在x2∈R，使得成立？若存在，求实数m的取值范围；若不存在，请说明理由．
参考答案与试题解析
2020-2021学年四川省成都市高一（上）期末数学试卷
一、选择题
1.
【答案】
D
【考点】
交、并、补集的混合运算
【解析】
利用并集定义先求出M∪N，再由补集定义求出∁U(M∪N)．
【解答】
∵ 全集U＝{1, 2, 3, 4, 5}，集合M＝{2, 3, 4}，N＝{3, 4}，
∴ M∪N＝{2, 3, 4}，
∴ ∁U(M∪N)＝{1, 5}．
2.
【答案】
B
【考点】
判断两个函数是否为同一函数
【解析】
根据两个函数的定义域和解析式都相同，即可判断它们是相等函数．
【解答】
对于A，函数y＝＝|x|(x∈R)，与y＝x(x∈R)的解析式不同，不是相等函数；
对于B，函数y＝＝x(x∈R)，与y＝x(x∈R)的定义域相同，解析式也相同，是相等函数；
对于C，函数y＝＝x(x≥0)，与y＝x(x∈R)的定义域不同，不是相等函数；
对于D，函数y＝＝x(x≠0)，与y＝x(x∈R)的定义域不同，不是相等函数．
3.
【答案】
A
【考点】
任意角的三角函数
【解析】
由题意利用任意角的三角函数的定义，即可求解．
【解答】
∵ 角α的顶点与直角坐标系的原点重合，
始边与x轴的非负半轴重合，且．
角α的终边上有一点P(x, 3)，
∴ csα＝＝-，可得x<0，
整理可得x2＝，解得x＝−4．
4.
【答案】
B
【考点】
求函数的值
分段函数的应用
函数的求值
【解析】
根据题意，先求出f(0)的值，再计算可得答案．
【解答】
根据题意，函数，则f(0)＝e0+2＝3，
则f（f(0)）＝f(3)＝lg28＝3，
5.
【答案】
D
【考点】
扇形面积公式
【解析】
设扇形的半径为r，再根据扇形的面积公式求出r的值即可．
【解答】
设扇形的半径为r，
∵ 扇形的圆心角为30∘，面积为3πcm2，
∴ ＝3π，
解得r＝6．
6.
【答案】
C
【考点】
函数零点的判定定理
【解析】
连续f(x)＝lnx+2x−9，则f(x)是(0, +∞)上的增函数，x0是f(x)的零点，由f(3)f(4)<0，可得结论．
【解答】
设f(x)＝lnx+2x−9，显然f(x)是(0, +∞)上的增函数，x0是连续函数f(x)的零点．
因为f(3)＝ln3+2×3−9＝ln3−3<0，f(4)＝ln4+2×4−9＝lln4−1>0，
f(3)f(4)<0，
故x0∈(3, 4)，
7.
【答案】
A
【考点】
余弦函数的单调性
【解析】
首先，令2kπ≤2x−≤2kπ+π，k∈Z，然后解不等式，确定函数的单调减区间即可．
【解答】
令2kπ≤2x−≤2kπ+π，k∈Z，
∴ 2kπ+≤2x≤2kπ+，
∴ kπ+≤x≤kπ+，
∴ f(x)的递减区间[kπ+，kπ+]，(k∈Z)，
8.
【答案】
C
【考点】
函数的图象与图象的变换
【解析】
根据题意，分析f(x)的奇偶性可以排除AB，求出f(2)的值排除D，即可得答案．
【解答】
根据题意，函数f(x)＝，有3|x|−3≠0，解可得x≠±1，
即函数的定义域为{x|x≠±1}，
有f(−x)＝＝f(x)，f(x)为偶函数，排除AB，
又由f(2)＝＝>0，排除D，
9.
【答案】
A
【考点】
函数y=Asin（ωx+φ）的图象变换
【解析】
由题意利用函数y＝Asin(ωx+φ)的图象变换规律求得g(x)的图象，可得的值．
【解答】
把函数的函数f(x)图象上各点的横坐标伸长到原来的2倍（纵坐标不变），
可得y＝2sin（+）的图象；
再将所得到的图象向右平移个单位长度，最后得到函数y＝g(x)＝2sin（-+）＝2sin（+）的图象，
则＝2sin＝1，
10.
【答案】
B
【考点】
复合函数的单调性
【解析】
由题意利用复合函数的单调性，指数函数、二次函数的性质，求得a的范围．
【解答】
∵ 函数 在[1, 2]上单调递减，
∴ g(x)＝x2+ax−1 在[1, 2]单调递增，∴ -≤1，求得a≥−2，
11.
【答案】
A
【考点】
对数值大小的比较
【解析】
利用不等式的性质、对数函数的单调性即可得出．
【解答】
a＝＝<，b＝lg32>lg3＝；
ln2＝>＝lg32，
故a12.
【答案】
D
【考点】
求函数的值
函数的求值
【解析】
先求出函数定义域，然后对函数进行化简，结合函数单调性得到关于x的不等式，再求出x的范围．
【解答】
由且|x+1|−1≠0，得−1故函数定义域(−1, 0)∪(0, 1)，
函数＝lg−x在(−1, 0)，(0, 1)上单调递减，
由≥0得，f(2x−1)≥f（），
所以−1<2x−1<1且2x−1≠0，
解得，0二、填空题
【答案】
-
【考点】
运用诱导公式化简求值
【解析】
由条件利用诱导公式进行化简所给的式子，可得结果．
【解答】
tan330∘＝tan(360∘−30∘)＝−tan30∘＝-，
【答案】
【考点】
指数函数的单调性与特殊点
指数函数的图象与性质
【解析】
令指数等于零，求得x、y的值，可得它的图象经过定点的坐标．
【解答】
对于函数y＝a2x−1+1(a>0且a≠1)的图象，
令2x−1＝0，求得x＝，y＝2，可得它的图象经过定点（，2)．
再根据它的图象恒过定点P(x0, y0)，则x0＝，
【答案】
【考点】
奇偶性与单调性的综合
【解析】
根据函数奇偶性和单调性之间的关系，即可得到结论．
【解答】
因为对区间(−∞, 0]上的任意x1，x2，当x1≠x2时，都有，
所以函数f(x)在(−∞, 0]上单调递减，
因为f(x)是定义在R上的偶函数，
若实数t满足f(2t+1)≤f(t−3)，
则|2t+1|≤|t−3|，
两边平方得，3t2+10t−8≤0，
解得，．
【答案】
【考点】
函数y=Asin（ωx+φ）的图象变换
【解析】
直接利用正弦型函数的性质的应用和函数的图象的平移变换的应用求出结果．
【解答】
∵ 函数在上单调，
所以，
即T，
由于函数f(x)的图象向右平移4π个单位长度后与原来的图象重合．
所以4π＝nT，
当n＝1时，
则T＝4，
整理得ω＝，
则f(x)＝sin（），
由于不等式成立，
故(k∈Z)，
解得(k∈Z)，
由于x∈(0, 4π)，
当k＝1时，．
三、解答题：
【答案】
（1）原式＝．
（2）原式＝．
【考点】
有理数指数幂的运算性质及化简求值
对数的运算性质
【解析】
利用指数、对数的性质、运算法则直接求解．
【解答】
（1）原式＝．
（2）原式＝．
【答案】
（1）由tanθ＝−2，得sinθ＝−2csθ．
∵ sin2θ+cs2θ＝1，
∴ ．
∵ ，
∴ sinθ>0，csθ<0．
∴ ，．
（2）原式＝，
∵ tanθ＝−2，
∴ 原式＝．
【考点】
三角函数的恒等变换及化简求值
同角三角函数间的基本关系
【解析】
(Ⅰ)利用同角三角函数关系结合三角函数在各个象限的符号，求出sinθ，csθ即可；
(Ⅱ)利用诱导公式将原式化简，再利用弦化切转化为tanθ，求解即可．
【解答】
（1）由tanθ＝−2，得sinθ＝−2csθ．
∵ sin2θ+cs2θ＝1，
∴ ．
∵ ，
∴ sinθ>0，csθ<0．
∴ ，．
（2）原式＝，
∵ tanθ＝−2，
∴ 原式＝．
【答案】
（1）证明：任取x1，x2∈R，且x1则＝．
∵ x1又∵ ，
∴ f(x1)−f(x2)<0，即f(x1)∴ 函数f(x)在R上单调递增．
（2）令t＝f(x)，函数g(x)＝lg3f(x)化为h(t)＝lg3t．
由(Ⅰ)知当x∈[1, 3]时，函数f(x)单调递增．
∴ 当x＝1时，函数f(x)有最小值；
当x＝3时，函数f(x)有最大值．∴ ．
又函数h(t)＝lg3t在上单调递增，
∴ 当，即x＝1时，函数h(t)有最小值−1，即g(x)有最小值−1；
当，即x＝3时，函数h(t)有最大值−2+lg37，即g(x)有最大值−2+lg37．
【考点】
函数单调性的性质与判断
函数的最值及其几何意义
【解析】
(Ⅰ)任取x1，x2∈R，且x1(Ⅱ)令t＝f(x)，函数g(x)＝lg3f(x)化为h(t)＝lg3t．利用函数的单调性求解函数的最值，推出结果即可．
【解答】
（1）证明：任取x1，x2∈R，且x1则＝．
∵ x1又∵ ，
∴ f(x1)−f(x2)<0，即f(x1)∴ 函数f(x)在R上单调递增．
（2）令t＝f(x)，函数g(x)＝lg3f(x)化为h(t)＝lg3t．
由(Ⅰ)知当x∈[1, 3]时，函数f(x)单调递增．
∴ 当x＝1时，函数f(x)有最小值；
当x＝3时，函数f(x)有最大值．∴ ．
又函数h(t)＝lg3t在上单调递增，
∴ 当，即x＝1时，函数h(t)有最小值−1，即g(x)有最小值−1；
当，即x＝3时，函数h(t)有最大值−2+lg37，即g(x)有最大值−2+lg37．
【答案】
（1）由题意，得P(t)＝a(1−2.47%)t，t∈N*，
化简得P(t)＝0.9753ta，t∈N*，
∴ P(800)＝0.9753800a，
∴ 经过800年后辐射物中锶90的剩余量为0.9753800a吨．
（2）由(Ⅰ)，知P(t)＝0.9753ta，t∈N*，
由题意，得0.9753ta<0.0846a，
不等式两边同时取对数，得ln0.9753t化简，得tln0.9753由参考数据，得−0.03t<−2.47．
∴ ，
又∵ ，
∴ 事故所在地至少经过83年才能再次成为人类居住的安全区．
【考点】
根据实际问题选择函数类型
【解析】
(Ⅰ)利用每年的衰减率为2.47%，即可得到P(t)的表达式，然后令t＝800，代入求解即可；
(Ⅱ)根据题意列出不等式0.9753ta<0.0846a，两边同时取自然对数，结合题中的数据进行分析求解即可．
【解答】
（1）由题意，得P(t)＝a(1−2.47%)t，t∈N*，
化简得P(t)＝0.9753ta，t∈N*，
∴ P(800)＝0.9753800a，
∴ 经过800年后辐射物中锶90的剩余量为0.9753800a吨．
（2）由(Ⅰ)，知P(t)＝0.9753ta，t∈N*，
由题意，得0.9753ta<0.0846a，
不等式两边同时取对数，得ln0.9753t化简，得tln0.9753由参考数据，得−0.03t<−2.47．
∴ ，
又∵ ，
∴ 事故所在地至少经过83年才能再次成为人类居住的安全区．
【答案】
（1）由题意，得A＝2，．
∴ T＝π，．
∴ f(x)＝2sin(2x+φ)．
又函数f(x)的图象经过点(0, −1)，则2sinφ＝−1．
由，得．
∴ ．
（2）由题意，关于x的方程f(x)−k＝0在上有且仅有两个实数根x1，x2，
即函数y＝f(x)与y＝k的图象在上有且仅有两个交点．
由(Ⅰ)知．令，则y＝2sint．
∵ ，
∴ ．
则y∈[−2, 2]．其函数图象如图所示．由图可知，实数k的取值范围为．
①当k∈[1, 2)时，t1，t2，关于对称，则．
解得．
②当时，t1，t2关于对称，则．
解得．
综上，实数k的取值范围为，x1+x2的值为或．
【考点】
正弦函数的图象
由y=Asin（ωx+φ）的部分图象确定其解析式
【解析】
(Ⅰ)由函数的图象的顶点坐标求出A，由周期求出ω，由特殊点的坐标求出φ的值，可得f(x)的解析式．
(Ⅱ)由题意可得f(x)的图象和直线y＝k在区间上有且仅有两个交点，再根据函数y＝Asin(ωx+φ)的图象和性质，求得实数k的取值范围，并求出x1+x2的值．
【解答】
（1）由题意，得A＝2，．
∴ T＝π，．
∴ f(x)＝2sin(2x+φ)．
又函数f(x)的图象经过点(0, −1)，则2sinφ＝−1．
由，得．
∴ ．
（2）由题意，关于x的方程f(x)−k＝0在上有且仅有两个实数根x1，x2，
即函数y＝f(x)与y＝k的图象在上有且仅有两个交点．
由(Ⅰ)知．令，则y＝2sint．
∵ ，
∴ ．
则y∈[−2, 2]．其函数图象如图所示．由图可知，实数k的取值范围为．
①当k∈[1, 2)时，t1，t2，关于对称，则．
解得．
②当时，t1，t2关于对称，则．
解得．
综上，实数k的取值范围为，x1+x2的值为或．
【答案】
（1）由函数的定义域为R，
则不等式ax2−2ax+1≥0对任意x∈R都成立，
①当a＝0时，1≥0显然成立；
②当a≠0时，欲使不等式ax2−2ax+1≥0对任意x∈R都成立，
则，解得0综上，实数a的取值范围为[0, 1]；
（2）当a＝1时，．
∴ 当x∈R时，f(x)min＝0．
令．可得函数t＝3x−3−x在x∈[−1, 1]上递增，则，
∴ 9x+9−x+m(3x−3−x)−1＝t2+mt+1，
令h(t)＝t2+mt+1，．
若存在实数m满足对任意x1∈[−1, 1]，都存在x2∈R，使得成立，
则只需h(t)min≥0．
①当即时，函数h(t)在上单调递增．
则．解得，与矛盾；
②当即时，函数h(t)在上单调递减，在上单调递增，
则，解得−2≤m≤2；
③当即时，函数h(t)在上单调递减．
则．解得，与矛盾．
综上，存在实数m满足条件，其取值范围为[−2, 2]．
【考点】
函数的定义域及其求法
函数恒成立问题
【解析】
(Ⅰ)由题意可得ax2−2ax+1≥0对任意x∈R都成立，讨论a＝0和a>0，△≤0，解不等式可得所求范围；
(Ⅱ)先求得f(x)min＝0，令，h(t)＝t2+mt+1，，由题意可得h(t)min≥0，讨论函数H(t)的对称轴和区间的关系，结合单调性，求得最值，解不等式可得所求范围．
【解答】
（1）由函数的定义域为R，
则不等式ax2−2ax+1≥0对任意x∈R都成立，
①当a＝0时，1≥0显然成立；
②当a≠0时，欲使不等式ax2−2ax+1≥0对任意x∈R都成立，
则，解得0综上，实数a的取值范围为[0, 1]；
（2）当a＝1时，．
∴ 当x∈R时，f(x)min＝0．
令．可得函数t＝3x−3−x在x∈[−1, 1]上递增，则，
∴ 9x+9−x+m(3x−3−x)−1＝t2+mt+1，
令h(t)＝t2+mt+1，．
若存在实数m满足对任意x1∈[−1, 1]，都存在x2∈R，使得成立，
则只需h(t)min≥0．
①当即时，函数h(t)在上单调递增．
则．解得，与矛盾；
②当即时，函数h(t)在上单调递减，在上单调递增，
则，解得−2≤m≤2；
③当即时，函数h(t)在上单调递减．
则．解得，与矛盾．
综上，存在实数m满足条件，其取值范围为[−2, 2]．