

2020-2021学年山东省潍坊市高二(上)10月新高考质量测评数学试卷人教B版
展开
这是一份2020-2021学年山东省潍坊市高二(上)10月新高考质量测评数学试卷人教B版,共15页。试卷主要包含了选择题,多选题,填空题,解答题等内容,欢迎下载使用。
1. 点P3,4,−5关于xOz平面对称的点的坐标是( )
A.3,4,5B.3,−4,−5C.−3,4,−5D.−3,−4,5
2. 如图,一个水平放置的平面图形的直观图是一个底角为45∘的等腰梯形,已知直观图OA′B′C′的面积为4,则该平面图形的面积为( )
A.2B.42 C.82D.22
3. 如图,在三棱锥A−BCD中,点F在棱AD上,且AF=3FD,E为BC中点,则FE→等于( )
A.−12AC→−12AB→+34AD→
B.12AC→+12AB→−34AD→
C.−12AC→+12AB→−23AD→
D.12AC→−12AB→+23AD→
4. 已知α⊥β且α∩β=l,m⊂α,则“m⊥β”是“m⊥l”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
5. 现有同底等高的圆锥和圆柱,已知圆柱的轴截面是边长为2的正方形,则圆锥的侧面积为( )
A.3πB.3π2C.5π2D.5π
6. 在我们身边,随处都可以看到各种物体的影子.现有一边长为5米的正方形遮阳布,要用它搭建一个简易遮阳棚,正方形遮阳布所在平面与东西方向的某一条直线平行.设正南方向射出的太阳光线与地面成60∘角,若要使所遮阴影面的面积最大,那么遮阳布所在平面与阴影面所成角的大小为( )
A.30∘B.45∘ C.60∘D.75∘
7. 将边长为2的正方形ABCD沿对角线AC折起,使得BD=2,则异面直线AB和CD所成角的余弦值为( )
A.12B.22C.32D.63
8. 如图,在三棱锥P−ABC中,BC⊥平面PAC,PA⊥AB,PA=AB=4,且E为PB的中点,AF⊥PC于F,当AC变化时,则三棱锥P−AEF体积的最大值是( )
A.223B.2C.423D.523
二、多选题
下面关于空间几何体叙述不正确的是( )
A.底面是正多边形的棱锥是正棱锥
B.棱柱的侧面都是平行四边形
C.直平行六面体是长方体
D.直角三角形以其一边所在直线为轴旋转一周形成的几何体是圆锥
设a→,b→,c→是空间的一组基底,则下列结论正确的是( )
A.a→,b→,c→可以为任意向量
B.对空间任一向量p→,存在唯一有序实数组x,y,z,使p→=xa→+yb→+zc→
C.若a→⊥b→,b→⊥c→,则a→⊥c→
D.a→+2b→,b→+2c→,c→+2a→可以作为构成空间的一组基底
如图,有一正四面体形状的木块,其棱长为a,点P是△ACD的中心.劳动课上,需过点P将该木块锯开,并使得截面平行于棱AB和CD,则下列关于截面的说法中正确的是( )
A.截面与侧面ABC的交线平行于侧面ABD
B.截面是一个三角形
C.截面是一个四边形
D.截面的面积为a24
如图,已知二面角A−BD−C的大小为π3,G,H分别是BC,CD的中点,E,F分别在AD,AB上,AEAD=AFAB=13,且AC⊥平面BCD,则以下说法正确的是( )
A.E,F,G,H四点共面
B.FG//平面ADC
C.若直线FG,HE交于点P,则P,A,C三点共线
D.若△ABD的面积为6,则△BCD的面积为3
三、填空题
在三棱锥P−ABC中,PA⊥平面ABC,∠PBA=45∘,∠PBC=60∘,则∠ABC为________.
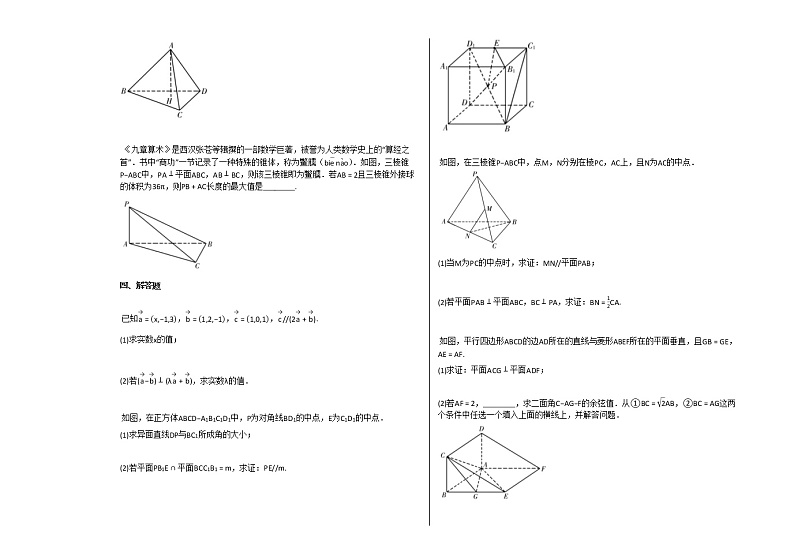
如图,已知平行六面体ABCD−A1B1C1D1中,AB=AD=2,AA1=4,∠BAA1=∠DAA1=∠BAD=60∘.M为CC1的中点,则AM长度为________.
如图,在四面体A−BCD中,△ABC为正三角形,四面体的高AH=3,若二面角A−BC−D的大小为π3,则△ABC的面积为________.
《九章算术》是西汉张苍等辑撰的一部数学巨著,被誉为人类数学史上的“算经之首”.书中“商功”一节记录了一种特殊的锥体,称为鳖臑(bie na).如图,三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC,则该三棱锥即为鳖臑.若AB=2且三棱锥外接球的体积为36π,则PB+AC长度的最大值是________.
四、解答题
已知a→=x,−1,3,b→=1,2,−1,c→=1,0,1,c→//(2a→+b→).
(1)求实数x的值;
(2)若(a→−b→)⊥(λa→+b→),求实数λ的值.
如图,在正方体ABCD−A1B1C1D1中,P为对角线BD1的中点,E为C1D1的中点.
(1)求异面直线DP与BC1所成角的大小;
(2)若平面PB1E∩平面BCC1B1=m,求证:PE//m.
如图,在三棱锥P−ABC中,点M,N分别在棱PC,AC上,且N为AC的中点.
(1)当M为PC的中点时,求证:MN//平面PAB;
(2)若平面PAB⊥平面ABC,BC⊥PA,求证:BN=12CA.
如图,平行四边形ABCD的边AD所在的直线与菱形ABEF所在的平面垂直,且GB=GE,AE=AF.
(1)求证:平面ACG⊥平面ADF;
(2)若AF=2,________,求二面角C−AG−F的余弦值.从①BC=2AB,②BC=AG这两个条件中任选一个填入上面的横线上,并解答问题.
如图,已知三棱台ABC−A1B1C1中,平面BCC1B1⊥平面ABC,△ABC是正三角形,侧面BCC1B1是等腰梯形,AB=2BB1=2B1C1=4,E为AC的中点.
(1)求证:AA1⊥BC;
(2)求直线EB1与平面ABB1A1所成角的正弦值.
如图,正方形ABCD和矩形ADEF所在的平面互相垂直,动点P在线段EF(包含端点E,F)上,M,N分别为AB,BC的中点,AB=2DE=2.
(1)若P为EF的中点,求点N到平面PDM的距离;
(2)设平面PDM与平面ABCD所成的锐角为θ,求csθ的最大值并求出此时点P的位置.
参考答案与试题解析
2020-2021学年山东省潍坊市高二(上)10月新高考质量测评数学试卷
一、选择题
1.
【答案】
B
【考点】
空间中的点的坐标
【解析】
两点关于xOz平面对称,则这两个点的横,竖坐标不变,纵坐标互为相反数,据此求解.
【解答】
解:在空间直角坐标系中,点P(3, 4, −5)关于xOz平面对称的点的坐标,y轴为相反数,x轴与z轴坐标不变,
故对称点坐标为(3, −4, −5).
故选B.
2.
【答案】
C
【考点】
斜二测画法画直观图
【解析】
根据在斜二测画法中,原图面积与直观图的面积比值为22直接解题即可.
【解答】
解:根据斜二测画法的规则可知该平面图形是直角梯形,
∵ 在斜二测画法中,原图面积是直观图面积的22倍,
∴ 所求梯形的面积是22×4=82.
故选C.
3.
【答案】
B
【考点】
空间向量的加减法
平面向量的基本定理及其意义
【解析】
直接利用向量的线性运算FE→=AE→−AF→=12AB→+12AC→−34AD→=12AC→+12AB→−34AD→即可求出结果.
【解答】
解:在三棱锥A−BCD中,点F在AD上,且AF=3FD,E为BC中点,
所以FE→=AE→−AF→=12AB→+12AC→−34AD→
=12AC→+12AB→−34AD→.
故选B.
4.
【答案】
C
【考点】
必要条件、充分条件与充要条件的判断
空间中直线与平面之间的位置关系
【解析】
利用面面垂直线面垂直判定和性质和充要条件的定义即可判断.
【解答】
解:由于α⊥β,α∩β=l,m⊂α,
若m⊥l,根据线面垂直的判断定理,则m⊥β,
若m⊥β,根据线面垂直的性质定理,则m⊥l,
故平面α⊥β,α∩β=l,m⊂α,则“m⊥β”是“m⊥l”成立的充要条件.
故选C.
5.
【答案】
D
【考点】
柱体、锥体、台体的侧面积和表面积
【解析】
设圆柱底面半径是r,高是ℎ,因为轴截面正方形,那么2r=2,ℎ=2,根据勾股定理得到圆锥的母线长,最后根据圆锥的侧面积公式12lR,其中l为圆锥的底面周长,R为圆锥的母线长,即可得到答案.
【解答】
解:设圆柱底面半径是r,高是ℎ,
∵ 轴截面是正方形,
∴ 2r=2,ℎ=2,
∴ 圆锥的底面半径r=1,高ℎ=2,
∴ 圆锥的母线长为12+22=5,
圆锥的底面周长为2πr=2π,
∴ 圆锥的侧面积为12×2π×5=5π.
故选D.
6.
【答案】
A
【考点】
平行投影及平行投影作图法
【解析】
分析题意,作出草图,借助平行投影,即可求出结果.
【解答】
解:如图:
由题意可知,要使得阴影面积最大,此时遮阳布与光线的方向垂直,
即AB⊥AM,作EN//AB,
则EN⊥AM,由题意∠AMN=60∘,
所以∠ENM=30∘,
即遮阳布所在平面与阴影面所成角的大小为30∘.
故选A.
7.
【答案】
A
【考点】
异面直线及其所成的角
【解析】
正方形ABCD边长为2,根据三角形中位线定理,得到则FG∥CD,EG∥AB,进而得到∠FGE为异面直线AB与CD所成的角,是解答本题的关键.然后根据等腰直角三角形和正方形的性质,计算出△EFG各边的长,即可得到△EFG是等边三角形,从而得到答案.
【解答】
解:取AC,BD,BC中点依次为E,F,G,
连接BD,EF,EG,FG,DE,EB,
则FG//CD,EG//AB,
∴ ∠FGE为异面直线AB与CD所成的角.
正方形边长为2,则FG=22,EG=22,
在等腰直角三角形ABC中,
∵ AB=BC=2,
∴ AC=2.
∵ 点E为AC的中点,
∴ BE=12AC=1,
同理可得,DE=1.
∵ BE2+DE2=2=BD2,
∴ △BED是等腰直角三角形.
又∵ 点F为BD的中点,
∴ EF=12BD=22.
在△EFG中,FG=EG=EF=22,
∴ △EFG是等边三角形,
∴ ∠FGE=60∘,
∴ cs∠FGE=cs60∘=12.
故选A.
8.
【答案】
C
【考点】
柱体、锥体、台体的体积计算
【解析】
利用几何体的特征,表示体积,再设边长,并表示体积,利用函数求出最值即可.
【解答】
解:∵ BC⊥平面PAC,
∴ AC⊥BC.
设AC=x,则BC=16−x2,
∵ AF⊥PC,
∴ AF=4x16+x2,PF=1616+x2.
∵ E为PB中点,BC⊥平面PAC,
∴ VE−PAF的高ℎ=12BC=16−x22,
∴ VP−AEF=VE−PAF=13⋅ℎ⋅S△PAF
=13×16−x22×12×4x16+x2×1616+x2
=163⋅x16−x216+x2,
令t=16+x2≥16,
则VP−AEF=163×t−1632−tt
=163×1−16t32t−1,
令a=1t≤116,
则VP−AEF=163×(1−16a)(32a−1),
所以当a=364时,VP−AEF 取最大值为163×122=423.
故选C.
二、多选题
【答案】
A,C,D
【考点】
旋转体(圆柱、圆锥、圆台)
棱锥的结构特征
棱柱的结构特征
【解析】
利用棱,锥的定义判断即可.
【解答】
解:A,正棱柱的侧棱要垂直底面,故A不正确;
B,棱柱的侧面均是平行四边形,故B正确;
C,直平行六面体是底面是平行四边形的直四棱柱,故不一定是长方体,故C不正确;
D,直角三角形以其直角边所在直线为轴旋转一周形成的几何体是圆锥,故D不正确.
故选ACD.
【答案】
B,D
【考点】
空间向量的基本定理及其意义
【解析】
利用空间向量基底的条件即可判断.
【解答】
解:A,作为基底a→,b→,c→的空间向量不能共面,故A错误;
B,为空间向量的基本定理,故B正确;
C,若a→⊥b→,b→⊥c→,可能a→//c→,故C错误;
D,假设三个向量共面,则存在实数对x,y,使得c→+2a→=xa→+2b→+yb→+2c→,
则有x=2,2y=1,2x+y=0,方程组无解,可见三个向量不共面,可以作为基底,故D正确.
故选BD.
【答案】
A,C
【考点】
截面及其作法
【解析】
利用线面平行的判定与性质先完成截面,利用正四面体的性质得AB⊥CD,可得解.
【解答】
解:在△ACD中,过点P做EF//CD,分别交AC,AD于E,F,
由P为△ACD的中心,得EF=23CD,
在平面ABC,平面ABD内做EH//AB,FG//AB交BC,BD于H,G,
连接HG,则四边形EFGH为所求做的截面,
故EH//平面ABD,故A正确;
由正四面体得AB⊥CD可得截面为长方形,故B错误,C正确;
且EF=23a,EH=13a,所以截面面积为S=29a2,故D错误.
故选AC.
【答案】
A,C,D
【考点】
二面角的平面角及求法
平行公理
平面的基本性质及推论
【解析】
此题暂无解析
【解答】
解:A,由题意,G,H分别是BC,CD的中点,
则有GH//BD,且GH=12BD,
同样地,由E,F分别在AD,AB上,
且AEAD=AFAB=13可知EF//BD,且EF=13BD,
于是有GH//EF,所以E,F,G,H四点共面,故A正确;
B,由GH=12BD,EF=13BD可知四边形EFGH为梯形,
所以FG与EH相交,从而FG不可能与平面ADC平行,故B错误;
C,由F,G在平面ABC中,E,H在平面ACD中,可知若直线FG与HE相交于P,
则交点P在平面ABC与平面ACD的交线,即AC上,
所以P,A,C三点共线,故C正确;
D,由二面角A−BD−C大小为π3,AC⊥平面BCD,且△ABD的面积为6,
则有S△BCDS△ABD=csπ3,即S△BCD=12×S△ABD=3,故D正确.
综上,正确的选项是ACD.
故选ACD.
三、填空题
【答案】
45∘
【考点】
直线与平面所成的角
【解析】
由条件找出各个角,套公式csθ=csα⋅csβ,可得答案.
【解答】
解:如图所示,由已知条件可得∠PBA是PB与平面ABC所成的角,
∠PBC是PB与BC所成的角,∠ABC是BC与PB在平面ABC内射影AB所成的角,
∴ cs∠PBC=cs∠PBA⋅cs∠ABC,
即cs60∘=cs45∘×cs∠ABC,
∴cs∠ABC=1222=22.
又∵0∘
相关试卷
这是一份2020-2021学年山东省潍坊市高二(上)期中数学试卷人教A版,共7页。试卷主要包含了单项选择题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2020-2021学年山东省潍坊市高三(上)期中考试数学试卷人教B版,共16页。试卷主要包含了选择题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2020-2021学年山东省潍坊市高三(上)期末考试数学试卷人教B版,共15页。试卷主要包含了选择题,多选题,填空题,解答题等内容,欢迎下载使用。









