湘教版八年级上册2.5 全等三角形教学课件ppt

这是一份湘教版八年级上册2.5 全等三角形教学课件ppt，共31页。PPT课件主要包含了知识回顾，给出三个条件，2三条边，3三个角，1两角一边，4两边一角，边角边定理，用几何语言表达为，写出在哪两个三角形中，写出全等结论等内容，欢迎下载使用。

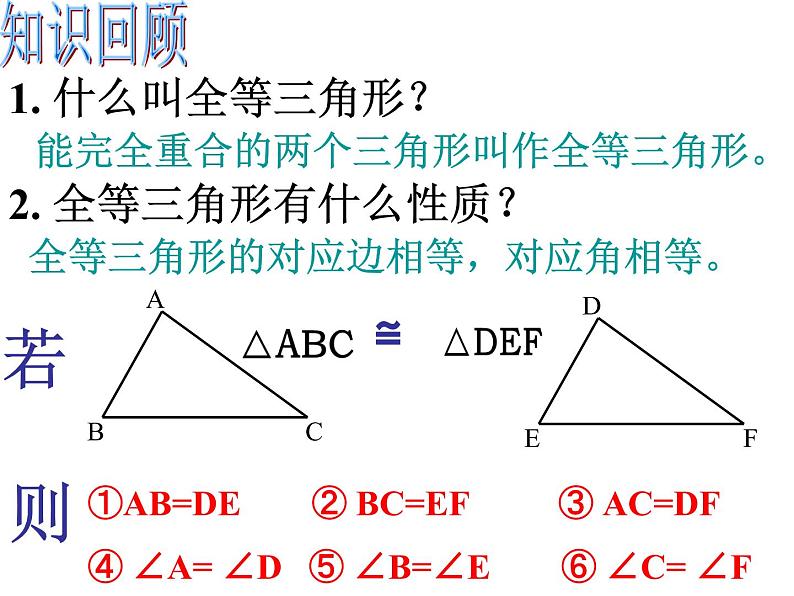
1. 什么叫全等三角形？
能完全重合的两个三角形叫作全等三角形。
2. 全等三角形有什么性质？
全等三角形的对应边相等，对应角相等。
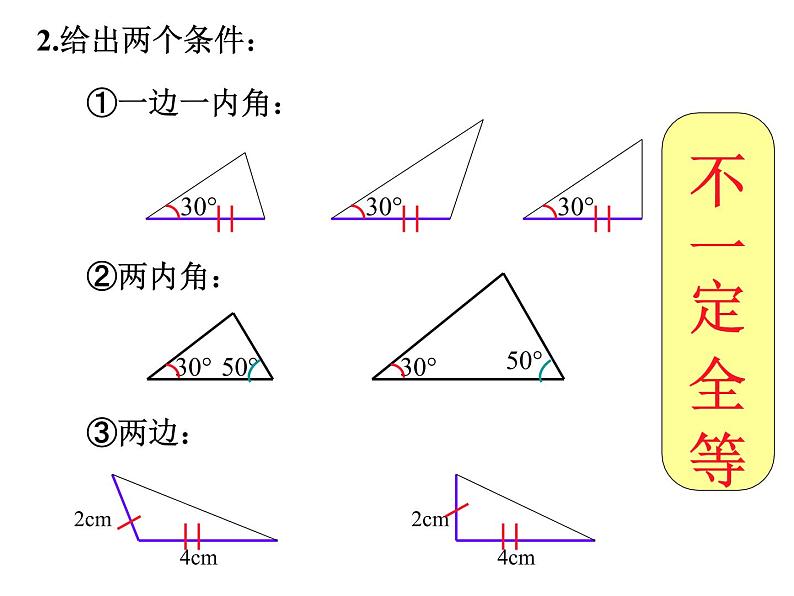
一个三角形包括三条边、三个内角共六个元素，那么两个三角形至少需要满足其中的几组元素相等才能说明它们全等呢？
下面我们来探讨这个问题
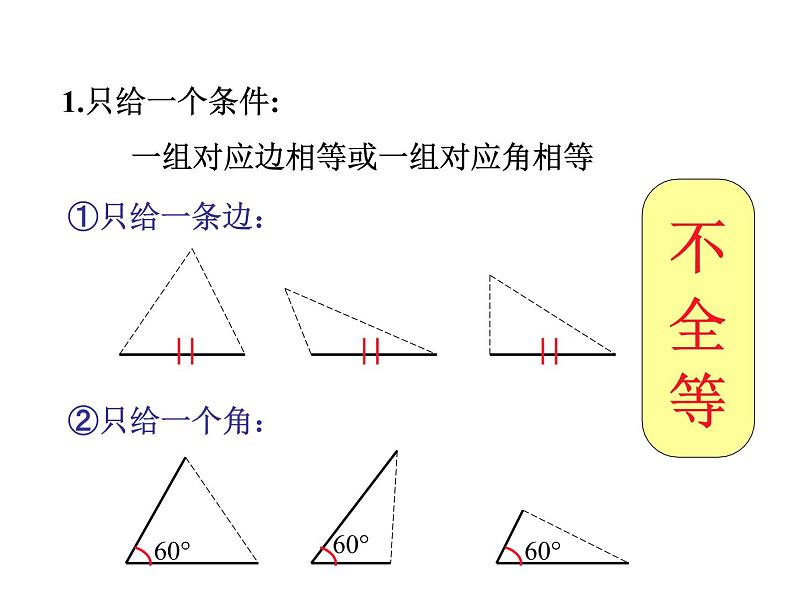
1.只给一个条件: 一组对应边相等或一组对应角相等
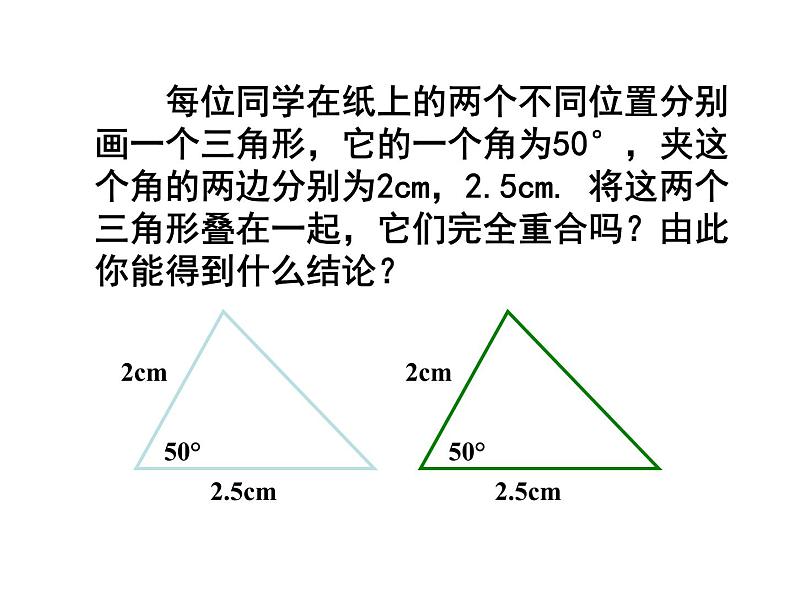
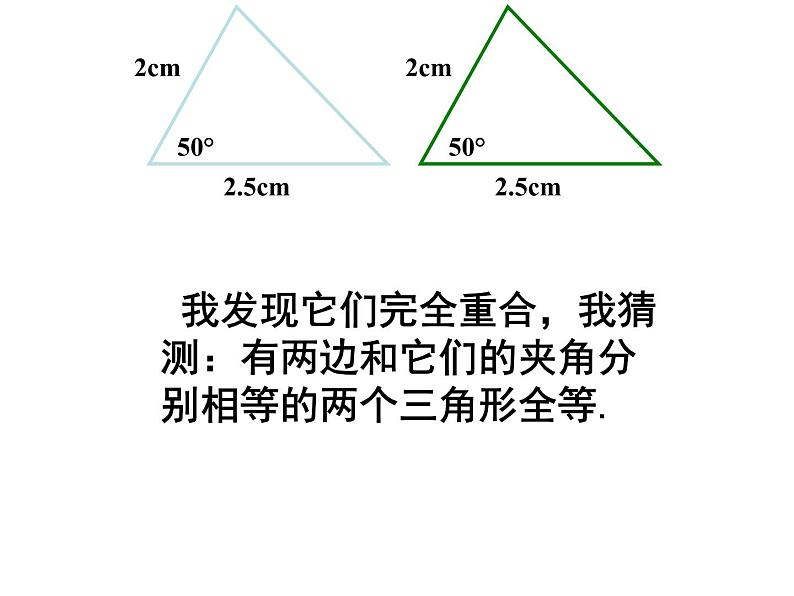
每位同学在纸上的两个不同位置分别画一个三角形，它的一个角为50°，夹这个角的两边分别为2cm，2.5cm. 将这两个三角形叠在一起，它们完全重合吗？由此你能得到什么结论？
我发现它们完全重合，我猜测：有两边和它们的夹角分别相等的两个三角形全等.
下面，我们从以下这几种情形来探讨这个猜测是否为真.
由于旋转不改变图形的形状和大小，
根据情形（1），（2）的结论得
将△ABC作关于直线BC的轴反射，
由于轴反射不改变图形的形状和大小，
如果两个三角形有两条边及其夹角分别对应相等，那么这两个三角形全等．
由此得到判定两个三角形全等的基本事实：
两边及其夹角分别相等的两个三角形全等.
通常可简写成“边角边”或“SAS”.
注意：边角边定理中的角是指两边的夹角。
在△ABC与△DEF中
AB=DE∠B=∠EBC=EF
∴△ABC≌△DEF（SAS）
例 已知：如图，AB和CD相交于O，且AO=BO， CO=DO. 求证：△ACO≌△BDO.
∴ △ACO≌△BDO.（SAS）
①准备条件： 证全等时要用的间接条件要先证好；
②三角形全等书写三步骤：
摆出三个条件用大括号括起来
1.如图：已知AB=CB ，∠ABD=∠CBD,问△ABD与△CBD全等吗？
△ ABD ≌△ CBD
∠ABD= ∠CBD(已知)
已知：如图, AB=CB,∠ABD=∠CBD。问AD=CD， BD 平分∠ ADC 吗？
已知:AD=CD,BD平分∠ADC.问∠A=∠C吗？
2. 如图，已知AC=BD，∠CAB= ∠DBA，你能判断BC=AD吗？说明理由。
点拨：要判定两个在角形中的两条线段相等或两个角相等，可以先证明它们所在的两个三角形全等，再根据全等三角形的性质（对应边相等、对应角相等）而得到。
解 △ABO≌△A′B′O，
2. 如图，AD∥BC，AD=BC. 问：△ADC和△CBA是全等三角形吗？为什么？
解 ∵ AD∥BC
∴ △ADC≌△CBA.（SAS）
∴∠DAC=∠BCA，（两直线平行，内错角相等）
3. 已知：如图，AB=AC，点E，F分别是AC， AB的中点. 求证：BE=CF.
解 ∵ AB=AC, 且 E，F分别是 AC，AB中点，
∴ △AEB≌△AFC.（SAS）
∴BE=CF(全等三角形的对应边相等）
2. 用尺规作图：已知两边及其夹角的三角形画三角形
1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)
审结论：△ABC≌ △DCB SAS
分析：审题： AB=DC，∠ABC= ∠ DCB.
1.如图：AB=DC，∠ABC= ∠ DCB，求证：△ABC≌ △DCB
审图：BC是△ABC与 △DCB的公共边。
AB=DC（已知） ∠ABC= ∠ DCB（已知） BC=CB（公共边） ∴ △ABC≌ △DCB （SAS）
注意：1、在哪两个三角形中？2、条件按边、角、边给出。3、对应。
证明：在△ABC和△DCB中
2.如图，已知AE = CF，AD∥BC，AD = CB， 那么△AFD与△CEB全等吗？
解：∵ AD∥BC （已知） ∴∠A = ∠C （两直线平行，内错角相等）. ∵AE = CF（已知） ∴AE-EF=CF-EF（等式的性质） 即AF=CE 在△AFD与△CEB中 AF = CE ∠A = ∠C AD = CB ∴ △AFD ≌ △CEB （SAS）.