2020-2021学年3.1 平方根评课ppt课件

这是一份2020-2021学年3.1 平方根评课ppt课件，共19页。PPT课件主要包含了你还会吗，生活中的数学，还认识老朋友吗，相信你能行，结识新朋友，找窍门，再结新朋友，训练思维，挑战自我等内容，欢迎下载使用。

　3 2 = , ( – 3)2 = ,
平方是0.01的数有 .
( – 0.1)2 = ,
平方是9的数有 .
一个正方形展厅的边长为7米，它的面积是 平方米.
一个正方形展厅的面积为49平方米，它的边长是 米.
0.1 2 = ,
2、我们已经学过哪几种数的运算？　 它们的运算结果分别叫什么？
3、加法和减法这两种运算之间有什么关系？乘法和除法之间呢？
答：它们之间均互为逆运算。
思考:乘方是不是也有逆运算呢？
　　　思考: 某家庭在装修儿童房时需铺地垫10.8平方米，刚好用去正方形的地垫30块，你能算出每块地垫的边长是多少吗？
分析：（１）每一块地垫的面积是多少平方米？
（２）什么数的平方等于0.36？
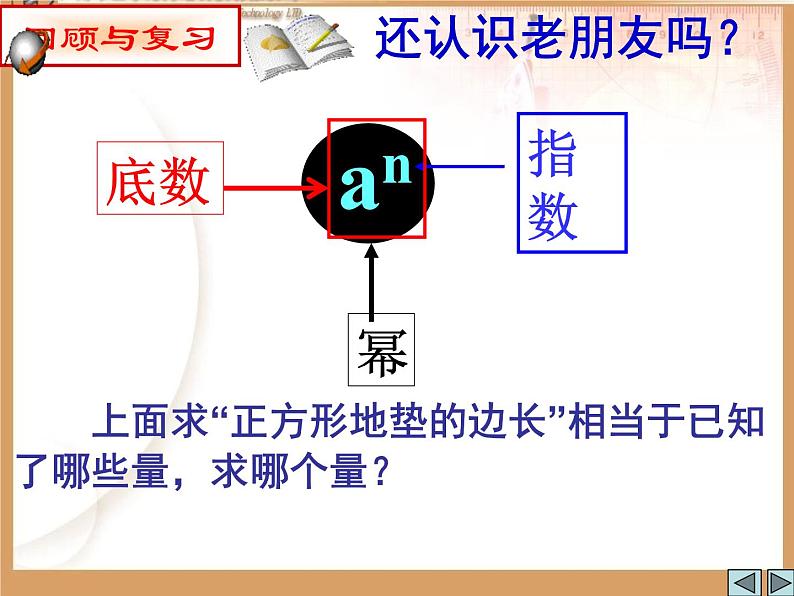
　　上面求“正方形地垫的边长”相当于已知了哪些量，求哪个量？
所以, ２ 是 ４的一个平方根,
一般地，如果有一个数r,使得ｒ２＝ａ,那么我们把r叫作a的一个平方根。
因为 ２ 2 = ４ ,
说出9、16、25、36、49的一个平方根
3.1 平方根（1）
4的平方根除2外，还有别的数吗？
　　一般地，如果r是正数a的一个平方根，那么a的平方根有且只有两个：r 与-r
想一想：正数a的两个平方根 有什么关系？
所以,– ２ 是 ４的一个平方根,
因为 (– ２ )2 =４,
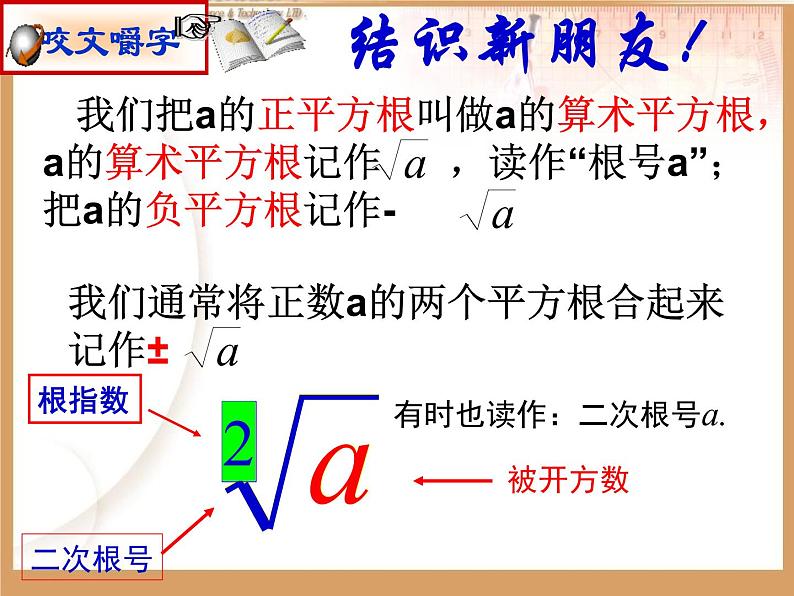
我们把a的正平方根叫做a的算术平方根，a的算术平方根记作 ，读作“根号a”；把a的负平方根记作-
有时也读作：二次根号a.
我们通常将正数a的两个平方根合起来记作±
如何快速求一个正数的平方根？
先求该正数的算术平方根，然后再找出它的负的平方根
所以－2也是4的一个平方根，记作- 　 =-2
例如　2是4的正的平方根，即４的算术平方根　　　　 记作 =2
思考:零有平方根吗?
零的平方根有且只有一个:是0, 记作 　　=0
思考:零有算术平方根吗?
规定:零的算术平方根是0
问:负数有平方根吗?为什么?
思考: 什么数一定有平方根?什么数一定 有算术平方根?
因为任何数的平方一定是非负数。
非负数一定有平方根；非负数一定有算术平方根．即式子　　中的ａ只能是非负数。
一个正数有两个平方根，它们互为相反数；
0有一个平方根，它是0本身；
平方和开平方互为逆运算.
求一个非负数的平方根的运算,叫做开平方.
我们可以通过平方运算来求一个数的平方根，也可以检验一个数是不是另一个数的平方根.
(1) 因为–64是负数,所以–64没有平方根;
(3) 因为(– 4 )2 = 16 > 0,所以（– 4）２有两个平方根,
(2) 0有一个平方根,它是0;
(4) 因为（ａ＋１）2≥ 0,所以（ａ＋１）2有平方根,
会有几个平方根？分别是什么？
例２ 分别求下列各数的平方根
解：因62=36,因此36的平方根是6和-6
1、平方根的概念和表示方法和开平方的概念；
3、平方和开平方互为逆运算；
即：如果一个数的平方等于a ，这个数就叫做a 的平方根。
求一个非负数的平方根的运算,叫做开平方.
一个正数有两个平方根，它们互为相反数；
课堂练习: P108页 练习题
4、已知一个数的两个平方根分别是 x +2 和 3x – 14，则该数为 。
2、一个数的平方根是它本身，这样的数有 ，一个正数有 个平方根，它们的和为 。
3、一个正方形展厅的面积为50平方米，它的边长是 米。
x +2 = – (3x – 14)