2020-2021学年5.1 任意角和弧度制课文ppt课件

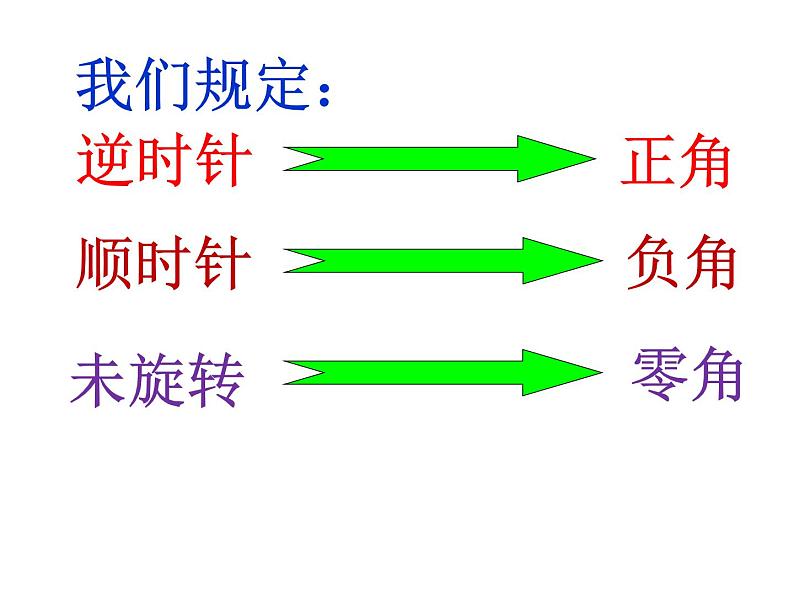
这是一份2020-2021学年5.1 任意角和弧度制课文ppt课件，共24页。PPT课件主要包含了逆时针，顺时针，未旋转，我们规定，任意角，请大家画出60°的角，一起来探究，课堂小结等内容，欢迎下载使用。
（一）那些年，我们一起学过的角
锐角 直角 钝角平角 周角
（二）说一说这些角的范围
实例1：在现实生活中有没有不在 范围内的角？
实例2：将时钟调快4小时，时针如何调？ 调慢4小时呢？
发现： 角是由“旋转”而来
实例1：转体720度、转体1080度这样的动作，这里的旋转量都比360度大，表明角具有任意性。实例2：顺时针、逆时针表明角具有方向性。因此，需要对角的概念进行推广.
O 叫做角α的顶点，OA叫做角α的始边，OB叫做角α的终边. ．
“旋转”形成角如图：一条射线的端点O，它从起始位置OA按逆时针方向旋转到终止位置OB，形成了一个角α．
用旋转来描述角，需要注意三个要素：旋转中心、旋转方向和旋转量
（2）旋转方向：旋转变换的方向分为逆时针和顺时针两种，这是一对意义相反的量，根据以往的经验，我们可以把一对意义相反的量用正负数来表示.
（1）旋转中心：作为角的顶点.
（3）旋转量：当旋转超过一周时，旋转量即超过360º，角度的绝对值可大于360º .于是就会出现720º ， － 540º15′等角度.
用“旋转”定义角之后，角的概念推广到了
手表快了1.5小时，为了将它校准 （时针1小时，分针转一圈）
将分针逆时针旋转 360+180  = 540°
手表慢了1.5小时，如何调？
将分针顺时针旋转 -360-180  = -540°

为了研究方便，我们往往在平面直角坐标系中来讨论角。
角的顶点与坐标原点重合，
角的始边与x轴的非负半轴重合.
那么，角的终边在第几象限，我们就说这个角是第几象限的角。
如果角的终边落在坐标轴上，则该角不属于任何一个象限.
 60 135  300330 390
请回答以下的角是第几象限的角：
将角按照上述方法放在直角坐标系中后，任意给定一个角，就有唯一的一条终边与之对应.反之，对于任意一条射线OB，以它为终边的角是否唯一确定？
那么终边相同的角有什么关系？
小球上记录了以下角度：210 、390、570 、750、-150 、-330、-510 、-690，判断它们的终边是否与30角的终边相同.
（1）观察：390, -330,-690，它们的终边都与30角的终边相同.
（2）探究： 390=30+ , 750=30+ , -330=30 - , -690=30- ， 30=30 + .
（3）结论：与30终边相同的角可以表示为： {β| β= 30 +k·360º, k∈Z} ，
即30与整数个周角的和.
写出与－60°终边相同的角的集合
｛β︱β= －60 °＋ k·360°,k∈Z｝
写出与0°终边相同的角的集合
｛β︱β= 0 °＋ k·360°,k∈Z｝
对于S={β| β=α+k·360º, k∈Z} 注意以下几点：① k∈Z，k > 0，表示在α的基础上逆时针旋转，k < 0 ，表示在α的基础上顺时针旋转，k = 0 ，即为α.② 终边相同的角不一定相等，终边相同的角有无限多个，它们相差360º的整数倍.
例. 在0º~360º范围内，找出与1125º终边相同的角，并判断它是哪个象限的角.
2. 任意角包括哪几类角？
1. 你知道角是如何推广的吗？
3. 象限角是如何定义的?
4. 终边相同的角的集合如何表示?
最后希望同学们珍惜时间，不负韶华!