高中数学苏教版必修13.4.1 函数与方程备课课件ppt

这是一份高中数学苏教版必修13.4.1 函数与方程备课课件ppt，共23页。PPT课件主要包含了-2-，知识梳理，双基自测，fx0，连续曲线，fx00，-3-，x10，-4-，一分为二等内容，欢迎下载使用。

1.函数的零点(1)函数零点的定义对于函数y=f(x)(x∈D),把使　　　　　成立的实数x叫做函数y=f(x)(x∈D)的零点. (2)函数零点的等价关系方程f(x)=0有实数根⇔函数y=f(x)的图象与　　　　有交点⇔函数y=f(x)有　　　　. (3)函数零点的判定(零点存在性定理)
　f(a)·f(b)<0
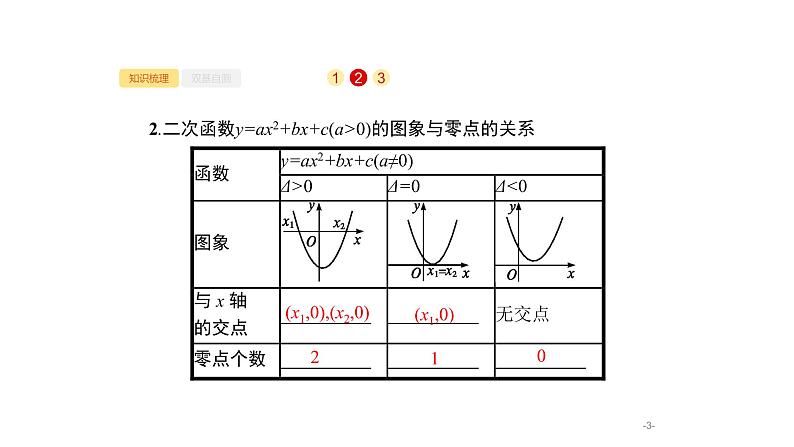
2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系
(x1,0),(x2,0)
3.二分法对于在区间[a,b]上连续不断且　　　　　　　　　的函数y=f(x),通过不断地把函数f(x)的零点所在的区间　　　　　　,使区间的两个端点逐步逼近　　　　,进而得到零点近似值的方法叫做二分法. 
f(a)·f(b)<0
1.下列结论正确的打“√”,错误的打“×”.(1)函数f(x)=x2-1的零点是(-1,0)和(1,0). (　　)(2)当b2-4ac<0时,二次函数y=ax2+bx+c(a≠0) 没有零点. (　　)(3)函数y=f(x)在区间(a,b)内有零点(函数图象是连续的),则f(a)·f(b)<0. (　　)(4)若函数f(x)在区间(a,b)内连续单调且f(a)·f(b)<0,则函数f(x)在区间[a,b]上有且只有一个零点.(　　)(5)函数y=2sin x-1的零点有无数多个. (　　)(6)只要函数有零点,我们就可以用二分法求出零点的近似值. (　　)
2.函数f(x)=-|x|- +3的零点所在的区间为(　　)A.(0,1)B.(1,2)C.(2,3)D.(3,4)
3.如果二次函数y=x2+mx+m+3有两个不同的零点,那么m的取值范围是(　　)A.(-2,6)B.[-2,6]C.{-2,6}D.(-∞,-2)∪(6,+∞)
4.当x∈R时,函数f(x)=x2-2x的零点的个数是(　　)A.0B.1C.2D.3
5.函数f(x)=ex+3x,则方程ex+3x=0实数解的个数是(　　)A.0B.1C.2D.3
(2)设定义域为(0,+∞)内的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)-ln x]=e+1,若x0是方程f(x)-f'(x)=e的一个解,则x0可能存在的区间是(　　)A.(0,1)B.(e-1,1)C.(0,e-1)D.(1,e)思考判断函数y=f(x)在某个区间上是否存在零点的常用方法有哪些?
例1(1)在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为(　　)
(2)令f(x)-ln x=k,则f(x)=ln x+k.由f[f(x)-ln x]=e+1,得f(k)=e+1.又f(k)=ln k+k=e+1,可知k=e.
解题心得判断函数y=f(x)在某个区间上是否存在零点,常用以下方法:(1)解方程:当对应方程易解时,可通过解方程,观察方程是否有根落在给定区间上.(2)利用函数零点的存在性定理进行判断:首先看函数y=f(x)在区间[a,b]上的图象是否连续,然后看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.(3)通过画函数图象,观察图象与x轴在给定区间上是否有交点来判断.
(2)已知函数f(x)=2x- -a的一个零点在区间(1,2)内,则实数a的取值范围是(　　)A.(1,3)B.(1,2)C.(0,3)D.(0,2)(3)函数f(x)=x2-3x-18在区间[1,8]上　　　　　零点.(填“存在”或“不存在”) 
对点训练1(1)函数f(x)=πx+lg2x的零点所在的区间为(　　)
(2)由条件可知f(1)f(2)<0,即(2-2-a)(4-1-a)<0,即a(a-3)<0,解得0(3)(方法一)∵f(1)=12-3×1-18=-20<0,f(8)=82-3×8-18=22>0,∴f(1)·f(8)<0,又f(x)=x2-3x-18在区间[1,8]上的图象是连续的,∴f(x)=x2-3x-18在区间[1,8]上存在零点.(方法二)令f(x)=0,得x2-3x-18=0,∴(x-6)·(x+3)=0.∴x=6或x=-3.∵x=6∈[1,8],x=-3∉[1,8],∴f(x)=x2-3x-18在区间[1,8]上存在零点.
例2(1)函数f(x)=2x|lg0.5x|-1的零点个数为 (　　)A.1B.2C.3 D.4(2)已知f(x)是定义在R上的偶函数,且对于任意的x∈[0,+∞),满足f(x+2)=f(x),若当x∈[0,2)时,f(x)=|x2-x-1|,则函数y=f(x)-1在区间[-2,4]上的零点个数为　　　　　. 思考判断函数零点个数的常用方法有哪些?
(2)由题意作出y=f(x)在区间[-2,4]上的图象,可知与直线y=1的交点共有7个,故函数y=f(x)-1在区间[-2,4]上的零点个数为7.
解题心得判断函数零点个数的方法:(1)解方程法:若对应方程f(x)=0可解时,通过解方程,则有几个解就有几个零点.(2)零点存在性定理法:利用定理不仅要判断函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点.(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,再看其交点的个数,其中交点的个数就是函数零点的个数.
(2)已知函数f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=2 017x+lg2 017x,则f(x)在R上的零点的个数为　　　　　. 
零点,则a的取值范围是(　　)A.[-1,0)B.[0,+∞)C.[-1,+∞)D.[1,+∞)思考已知函数有零点(方程有根),求参数的取值范围常用的方法有哪些?
解题心得已知函数有零点(方程有根),求参数的取值范围常用的方法:(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围.(2)分离参数法:先将参数分离,再转化成求函数值域问题加以解决.(3)数形结合法:先对解析式变形,在同一平面直角坐标系中画出函数的图象,再数形结合求解.