5.4　数系的扩充与复数的引入课件PPT

这是一份5.4　数系的扩充与复数的引入课件PPT，共21页。PPT课件主要包含了-2-，知识梳理，双基自测，a+bi，ac且bd，ac且b-d，-3-，-4-，复数的几何意义，-5-等内容，欢迎下载使用。
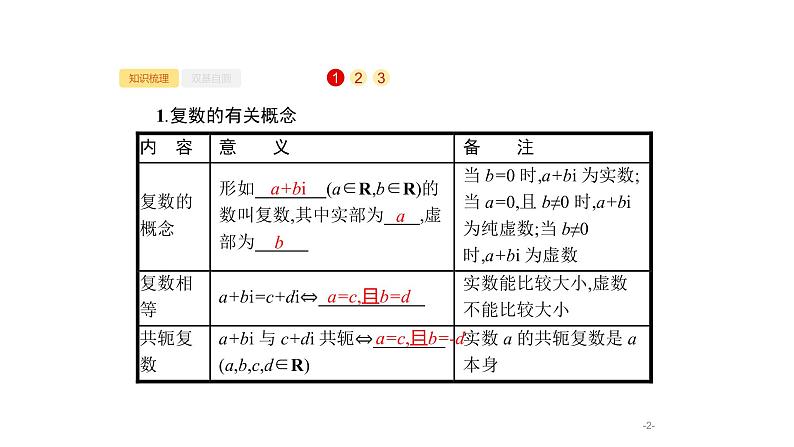
1.复数的有关概念
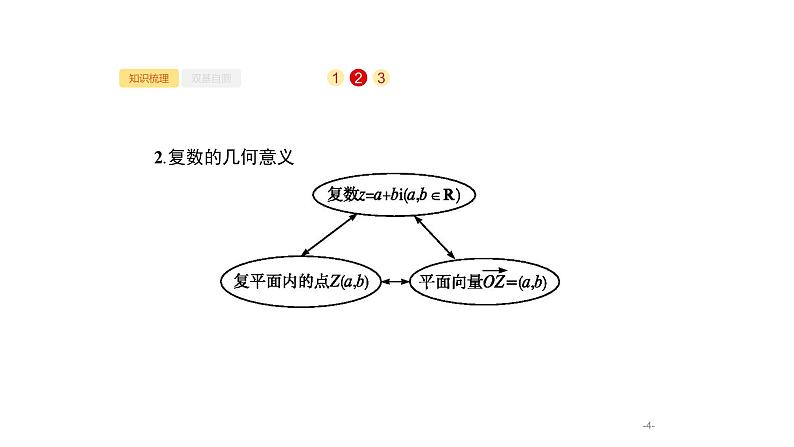
3.复数的运算(1)复数的加、减、乘、除运算法则设z1=a+bi,z2=c+di(a,b,c,d∈R),则①加法:z1+z2=(a+bi)+(c+di)=　　　　　　; ②减法:z1-z2=(a+bi)-(c+di)=　　　　　　; ③乘法:z1·z2=(a+bi)·(c+di)=　 　　　　　; 
(a+c)+(b+d)i
(a-c)+(b-d)i　
(ac-bd)+(ad+bc)i
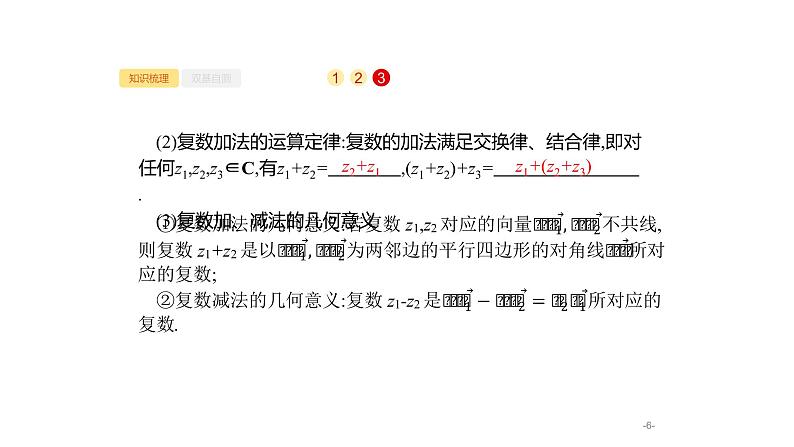
(2)复数加法的运算定律:复数的加法满足交换律、结合律,即对任何z1,z2,z3∈C,有z1+z2=　　　　,(z1+z2)+z3=　　　　　　　　. (3)复数加、减法的几何意义
z1+(z2+z3)
1.下列结论正确的打“√”,错误的打“×”.(1)若a∈C,则a2≥0. (　　)(2)已知z=a+bi(a,b∈R),当a=0时,复数z为纯虚数. (　　)(3)复数z=a+bi(a,b∈R)的虚部为bi. (　　)(4)方程x2+x+1=0没有解. (　　)(5)由于复数包含实数,在实数范围内两个数能比较大小,因此在复数范围内两个数也能比较大小. (　　)
2.设有下面四个命题
其中的真命题为(　　)A.p1,p3B.p1,p4C.p2,p3D.p2,p4
A.1+2iB.1-2iC.2+iD.2-i
5.设复数z满足(1+i)z=2i,则|z|=(　　)
6.已知(1+2i) =4+3i,则z=　　　　　. 
(2)已知a,b∈R,i是虚数单位,若(1+i)(1-bi)=a,则 的值为　　　.思考利用复数的四则运算求复数的一般方法是什么?
A.iB.1+iC.-iD.1-i
解题心得利用复数的四则运算求复数的一般方法:(1)复数的加法、减法、乘法运算可以类比多项式的运算.(2)复数的除法运算主要是利用分子、分母同乘分母的共轭复数进行运算化简.
对点训练1(1)已知a,b∈R,i是虚数单位,若a+i=2-bi,则(a+bi)2=(　　)A.3-4iB.3+4iC.4-3iD.4+3i
A.1+iB.1-iC.-1+iD.-1-i(3)设复数z满足(z-2i)(2-i)=5,则z=(　　)A.2+3iB.2-3iC.3+2iD.3-2i
p1:|z|=2; p2:z2=2i; p3:z的共轭复数为1+i; p4:z的虚部为-1.其中正确的是(　　)A.p2,p3B.p1,p2C.p2,p4D.p3,p4(3)已知复数z=(1+2i)(3-i),其中i为虚数单位,则z的实部是　　　　　. 思考求解与复数概念相关问题的基本思路是什么?
解题心得求解与复数概念相关问题的基本思路:复数的分类、复数的相等、复数的模、共轭复数以及求复数的实部、虚部都与复数的实部与虚部有关,所以解答与复数相关概念的问题时,需把所给复数化为代数形式,即a+bi(a,b∈R)的形式,再根据题意求解.
对点训练2(1)若复数z满足(3-4i)z=|4+3i|,则z的虚部为(　　)A.2+iB.2-iC.-1+iD.-1-i
例3(1)设i是虚数单位,则复数 在复平面内所对应的点位于(　　)A.第一象限B.第二象限C.第三象限D.第四象限(2)设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=(　　)A.-5B.5C.-4+iD.-4-i思考复数具有怎样的几何意义?几何意义的作用是什么?
=-1+i,对应点为(-1,1)在第二象限内.故选B.(2)由题意知:z2=-2+i.又z1=2+i,所以z1z2=(2+i)(-2+i)=i2-4=-5.故选A.
2.由于复数、点、向量之间建立了一一对应的关系,因此可把复数、向量与解析几何联系在一起,解题时可运用数形结合的方法,使问题的解决更加直观.