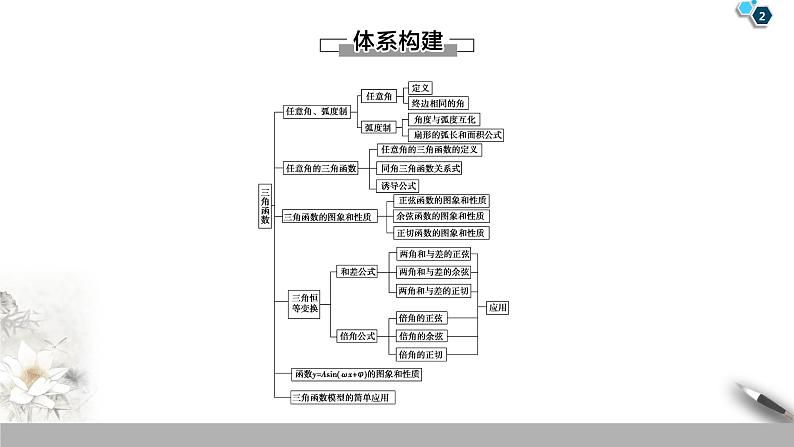
高中数学人教A版 (2019)必修 第一册第五章 三角函数本章综合与测试复习课件ppt

同角三角函数基本关系和诱导公式的应用

【例1】　(1)已知sin(－π＋θ)＋2cos(3π－θ)＝0，则＝________.

(2)已知f(α)＝.

①化简f(α)；

②若f(α)＝，且＜α＜，求cos α－sin α的值；

③若α＝－，求f(α)的值．

[思路点拨]　先用诱导公式化简，再用同角三角函数基本关系求值．

(1)　[由已知得－sin θ－2cos θ＝0，故tan θ＝－2，

则＝＝＝.]

(2)[解]　①f(α)＝＝sin α·cos α.

②由f(α)＝sin α·cos α＝可知，

(cos α－sin α)2＝cos2α－2sin α·cos α＋sin2α

＝1－2sin α·cos α＝1－2×＝，

又∵＜α＜，∴cos α＜sin α，

即cos α－sin α＜0，

∴cos α－sin α＝－.

③∵α＝－π＝－6×2π＋，

∴f＝cos·sin

＝cos·sin

＝cos·sin＝×＝.

1．牢记两个基本关系式sin2α＋cos2α＝1及＝tan α，并能应用两个关系式进行三角函数的求值、化简、证明．在应用中，要注意掌握解题的技巧．比如：已知sin α±cos α的值，可求cos αsin α.注意应用(cos α±sin α)2＝1±2sin αcos α.

2．诱导公式可概括为k·±α(k∈Z)的各三角函数值的化简公式．记忆规律是：奇变偶不变，符号看象限．

三角函数的图象变换问题

【例2】　(1)已知曲线C1：y＝cos x，C2：y＝sin，则下面结论正确的是(　　)

A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2

B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2

C．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2

D．把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2

(2)将函数y＝sin(2x＋φ)的图象沿x轴向左平移个单位长度后，得到一个偶函数的图象，则φ的一个可能取值为(　　)

A.　　　 B.

C．0   D．－

(1)D　(2)B　[(1)因为y＝sin＝cos＝cos，所以曲线C1：y＝cos x上各点的横坐标缩短到原来的倍，纵坐标不变，得到曲线y＝cos 2x，再把得到的曲线y＝cos 2x向左平移个单位长度，得到曲线y＝cos 2＝cos.

故选D.

(2)y＝sin(2x＋φ)的图象沿x轴向左平移个单位后

得y＝sin＝sin.若该函数为偶函数，

则＋φ＝kπ＋，k∈Z，故φ＝kπ＋.当k＝0时φ＝.故选B.]

1．函数y＝sin x的图象变换到y＝Asin(ωx＋φ)，x∈R图象的两种方法

2．对称变换

(1)y＝f(x)的图象y＝－f(x)的图象．

(2)y＝f(x)的图象y＝f(－x)的图象．

(3)y＝f(x)的图象y＝－f(－x)的图象．

1．将函数y＝2sin的图象向右平移个周期后，所得图象对应的函数为(　　)

A．y＝2sin   B．y＝2sin

C．y＝2sin   D．y＝2sin

D　[函数y＝2sin的周期为π，将函数y＝2sin的图象向右平移个周期即个单位长度，所得图象对应的函数为y＝2sin＝2sin，故选D.]

三角函数的性质

【例3】　(1)若函数f(x)＝3sin(2x＋θ)(0＜θ＜π)是偶函数，则f(x)在[0，π]上的单调递增区间是(　　)

A.   B.

C.   D.

(2)已知函数f(x)＝2sin＋a＋1(其中a为常数)．

①求f(x)的单调区间；

②若x∈时，f(x)的最大值为4，求a的值．

[思路点拨]　(1)先根据函数f(x)是偶函数，求θ，再依据单调性求增区间，最后与[0，π]求交集．

(2)①由2kπ－≤2x＋≤2kπ＋，k∈Z求增区间，

由2kπ＋≤2x＋≤2kπ＋，k∈Z求减区间．

②先求f(x)的最大值，得关于a的方程，再求a的值．

(1)B　[因为函数f(x)＝3sin(2x＋θ)(0＜θ＜π)是偶函数，

所以θ＝，f(x)＝3sin＝3cos 2x，

令2kπ－π≤2x≤2kπ，得kπ－≤x≤kπ，

可得函数f(x)的增区间为，k∈Z，

所以f(x)在[0，π]上的单调递增区间为.]

(2)[解]　①由－＋2kπ≤2x＋≤＋2kπ，k∈Z，解得－＋kπ≤x≤＋kπ，k∈Z，

∴函数f(x)的单调增区间为(k∈Z)，由＋2kπ≤2x＋≤＋2kπ，k∈Z，

解得＋kπ≤x≤＋kπ，k∈Z，

∴函数f(x)的单调减区间为(k∈Z)．

②∵0≤x≤，∴≤2x＋≤，

∴－≤sin≤1，

∴f(x)的最大值为2＋a＋1＝4，∴a＝1.

三角恒等变换的综合应用

【例4】　已知函数f(x)＝sinsin x－cos2x.

(1)求f(x)的最小正周期和最大值；

(2)讨论f(x)在上的单调性．

[解]　(1)f(x)＝sinsin x－cos2x

＝cos xsin x－(1＋cos 2x)

＝sin 2x－cos 2x－＝sin－，

因此f(x)的最小正周期为π，最大值为.

(2)当x∈时，0≤2x－≤π，从而

当0≤2x－≤，即≤x≤时，f(x)单调递增，

当≤2x－≤π，即≤x≤时，f(x)单调递减．

综上可知，f(x)在上单调递增；在上单调递减．

三角函数的图象和性质是三角函数的重要内容.如果给出的三角函数的表达式较为复杂，我们必须先通过三角恒等变换，将三角函数的表达式变形化简，然后根据化简后的三角函数，讨论其图象和性质.

1求三角函数的值域、单调区间、图象变换、周期性、对称性等问题，一般先要通过三角恒等变换将函数表达式变形为y＝Asinωx＋φ＋k或y＝Acosωx＋φ＋k等形式，让角和三角函数名称尽量少，然后再根据正、余弦函数基本性质和相关原理进行求解.

2要注意三角恒等变换中由于消项、约分、合并等原因，函数定义域往往会发生一些变化，所以一定要在变换前确定好原三角函数的定义域，并在这个定义域内分析问题.

2．已知函数f(x)＝.

(1)求f(x)的定义域及最小正周期；

(2)求f(x)的单调递减区间．

[解]　(1)由sin x≠0得x≠kπ(k∈Z)，

故f(x)的定义域为{x∈R|x≠kπ，k∈Z}．

因为f(x)＝

＝2cos x(sin x－cos x)

＝sin 2x－cos 2x－1

＝sin－1，

所以f(x)的最小正周期T＝＝π.

(2)函数y＝sin x的单调递减区间为2kπ＋，2kπ＋(k∈Z)．

由2kπ＋≤2x－≤2kπ＋，x≠kπ(k∈Z)，

得kπ＋≤x≤kπ＋(k∈Z)，

所以f(x)的单调递减区间为(k∈Z)．

三角函数的平面几何中的应用

【例5】　直角走廊的示意图如图所示，其两边走廊的宽度均为2米，过点P的一直线与走廊的外侧两边交于A，B两点，且与走廊的一边的夹角为θ.

(1)将线段AB的长度l表示为θ的函数；

(2)一根长度为5米的铁棒能否水平(即铁棒与地面平行)通过该直角走廊？并说明理由．(铁棒的粗细忽略不计)

[思路点拨]　(1)长度l可分成PA，PB两段分别用θ表示．

(2)判断铁棒能否水平通过该直角走廊需要比较铁棒长度与AB长度的最小值．

[解]　(1)由题意可知：

l＝＋＝，

其中0＜θ＜.

(2)l＝，

设t＝sin θ＋cos θ＝sin，

因为0＜θ＜，

所以＜θ＋＜，

所以t∈(1，]，

所以l＝＝.

因为t－在(1，]上是增函数，

所以t－的最大值为，

所以l＝的最小值为4.

因为4＞5，

所以长度为5米的铁棒能水平通过该直角走廊．

三角函数的实际应用多与最值有关，解决这类问题的一般步骤如下：

1审读题意，合理地选取“角”为自变量，建立三角函数关系式.

2利用和、差、倍、半角公式进行化简整理，通常要整理为y＝Asinωx＋φ＋b的形式.

3在符合实际问题意义的情形下求目标式的最值.

3．福建沿海的超强台风过后，当地人民积极恢复生产，焊接工王师傅每天都很忙碌．今天他遇到了一个难题：如图所示，有一块扇形钢板，半径为1米，圆心角θ＝，施工要求按图中所画的那样，在钢板OPQ上裁下一块平行四边形钢板ABOC，要求使裁下的钢板面积最大．试问王师傅如何确定A的位置，才能使裁下的钢板符合要求？最大面积为多少？

[解]　连接OA，设∠AOP＝α，过A作AH⊥OP，垂足为点H，在Rt△AOH中，OH＝cos α，AH＝sin α，所以BH＝＝sin α，所以OB＝OH－BH＝cos α－sin α，设平行四边形ABOC的面积为S，则S＝OB·AH＝·sin α＝sin αcos α－sin2α＝sin 2α－(1－cos 2α)＝sin 2α＋cos 2α－＝－＝sin－.

由于0＜α＜，所以＜2α＋＜π，

当2α＋＝，即α＝时，Smax＝－＝，所以当A是的中点时，所裁钢板的面积最大，最大面积为平方米．