



2022版高考数学一轮复习课件:经典微课4+探秘立体几何中的动态问题+【高考】
展开立体几何中的“动态”问题就变化起因而言大致可分为两类:一是平移;二是旋转.就所求变量而言可分为三类:一是相关线、面、体的测度;二是角度;三是距离.解决此类问题需要较高的空间想象能力与化归处理能力,如果我们能探寻运动过程中“静”的一面,动中求静,往往能以静制动、克难制胜.
一、去掉枝蔓见本质——大道至简在解决立体几何中的“动态”问题时,需从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序,是解决“动态”问题的关键.【例1】 如图,直线l⊥平面α,垂足为O,正方体ABCD-A1B1C1D1的棱长为2,点A是直线l上的动点,点B1在平面α内,则点O到线段CD1中点P的距离的最大值为________.
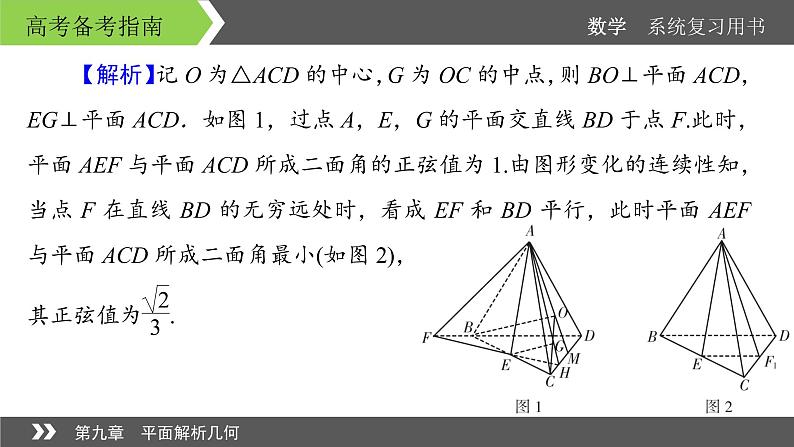
二、极端位置巧分析——穷妙极巧在解决立体几何中的“动态”问题时,对于移动问题,由图形变化的连续性,穷尽极端特殊之要害,往往能直取答案.【例2】 在正四面体A-BCD中,E为棱BC的中点,F为直线BD上的动点,则平面AEF与平面ACD所成二面角的正弦值的取值范围是________.
三、锁定垂面破翻折——独当一面在解决立体几何中的“动态”问题时,对于翻折或投影问题,若能抓住相关线或面的垂面,化空间为平面,则容易找到问题的核心.
【例3】 (多选)如图,在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下列命题中正确的是( )A.BM是定值B.点M在某个球面上运动C.存在某个位置,使DE⊥A1CD.存在某个位置,使MB∥平面A1DE
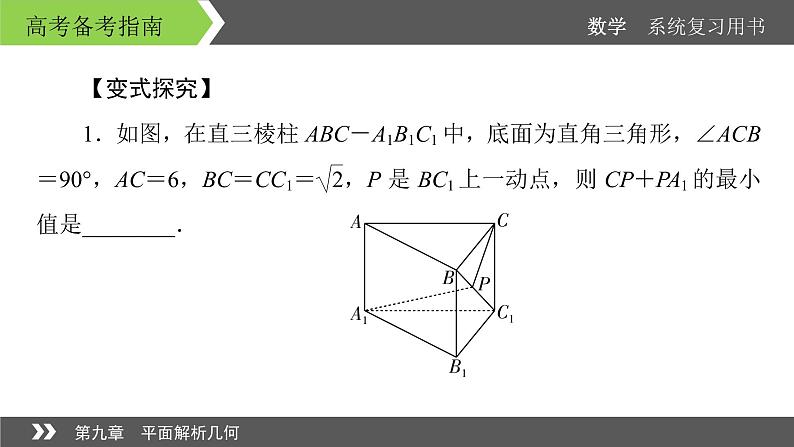
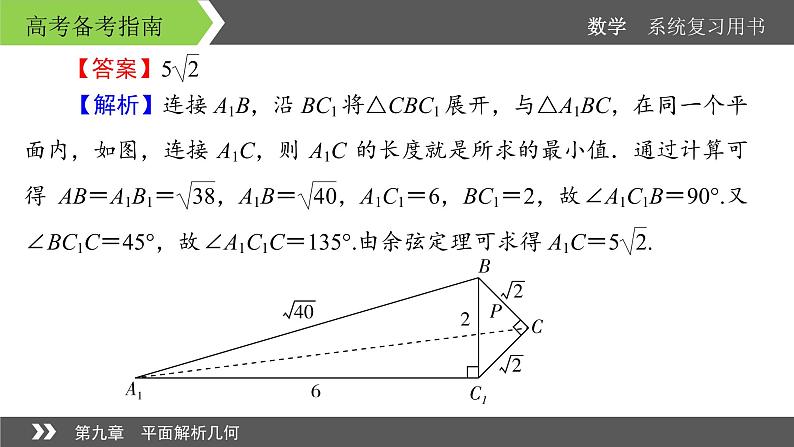
【变式探究】4. 如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外一点P和线段AC上一点D,满足PD=DA,PB=BA,则四面体P-BCD的体积的最大值是________.
专题四 微重点8 立体几何中的动态问题--高三高考数学复习-PPT: 这是一份专题四 微重点8 立体几何中的动态问题--高三高考数学复习-PPT,共60页。PPT课件主要包含了考点一,考点二,考点三,动点轨迹问题,展开问题,范围问题,专题强化练,在Rt△PDB中等内容,欢迎下载使用。
2024届高考数学一轮复习第6章思维深化微课堂立体几何中的动态问题课件: 这是一份2024届高考数学一轮复习第6章思维深化微课堂立体几何中的动态问题课件,共12页。
高考数学一轮复习第6章微课堂立体几何中的动态问题课件: 这是一份高考数学一轮复习第6章微课堂立体几何中的动态问题课件,共18页。












