2020-2021学年福建省泉州市高二（上）10月月考数学试卷人教A版

这是一份2020-2021学年福建省泉州市高二（上）10月月考数学试卷人教A版，共11页。试卷主要包含了选择题，多选题，解答题，填空题等内容，欢迎下载使用。

1. 直线l1：y=x+1中，若l1，l2关于x轴对称，则l2的倾斜角( )
A.π4B.3π4C.5π4D.−π4

2. 直线6x+8y−2=0与6x+8y−3=0间的距离为( )
A.110B.25C.1D.3

3. 在三棱锥O−ABC中，点D是棱AC的中点，若OA→=a→，OB→=b→，OC→=c→，则BD→等于( )

A.a→+b→−c→B.a→−b→+c→
C.−12a→+b→−12c→D.12a→−b→+12c→

4. 圆A，圆B，圆C两两外切，半径分别为2，3，10，则△ABC的形状是( )

A.等腰三角形B.锐角三角形C.钝角三角形D.直角三角形

5. 已知M4,−1，若点P是直线l： y=2x+3上的任意一点，则|PM|的最小值为( )
A.55B.1255C.121717D.25

6. 数学家欧拉在1765年提出定理：三角形的外心、重心、垂心位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线被后人称为三角形的欧拉线；已知△ABC的顶点B(−1, 0)，C(0, 2)，AB=AC，则△ABC的欧拉线方程为( )
A.2x+4y+3=0B.4x−2y−3=0C.2x+4y−3=0D.2x−4y−3=0

7. 如图所示，在长方体ABCD−A1B1C1D1中，AD=AA1=1，AB=2，点E是棱AB的中点，则点E到平面ACD1的距离为( )

A.13B.12C.16D.22

8. 若P为直线x−y+3=0上一个动点，从点P引圆x2+y2−2x=0的两条切线PM，PN（切点为M，N），则线段MN的长度的取值范围是( )

A.[142,2)B.142,2C.[7,2）D.7,2
二、多选题

已知直线l过点P−1,1，且与直线l1：2x−y+3=0以及x轴围成一个底边在x轴上的等腰三角形，则下列结论中正确的是( )

A.直线l与直线l1的斜率互为相反数
B.直线l与直线l1的倾斜角互补
C.这样的直线l有两条
D.直线l在y轴上的截距为−1

直线l过点P(1, 0)，且与以A(2, 1)，B(0, 3)为端点的线段有公共点，则直线l斜率可能是( )

A.−2B.12C.1D.3

已知向量a→=1,−1,m，b→=−2,m−1,2，则下列结论中正确的是( )
A.若|a→|=2，则m=±2
B.若a→⊥b→，则m=−1
C.若a→⋅b→=−1，则a→+b→=−1,−2,−2
D.不存在实数λ，使得a→=λb→

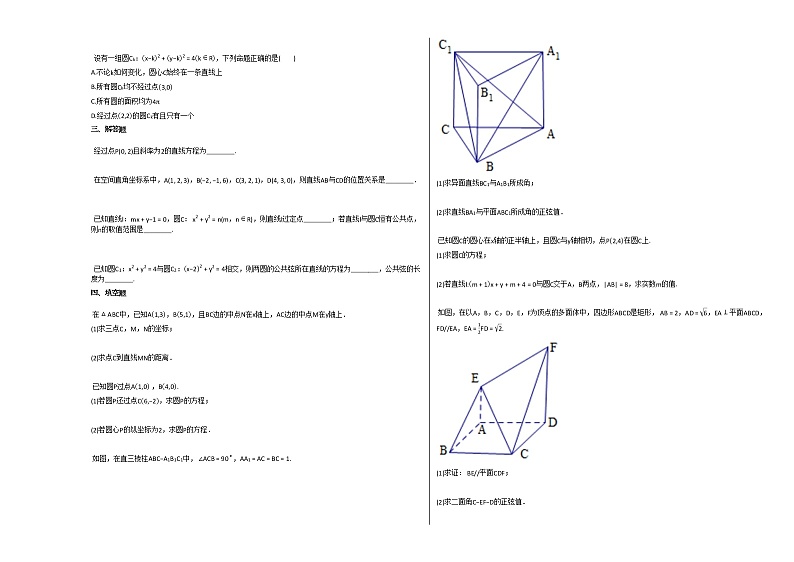
设有一组圆Ck：x−k2+y−k2=4k∈R，下列命题正确的是( )
A.不论k如何变化，圆心C始终在一条直线上
B.所有圆Ck均不经过点3,0
C.所有圆的面积均为4π
D.经过点2,2的圆Ck有且只有一个
三、解答题

经过点P(0, 2)且斜率为2的直线方程为________.

在空间直角坐标系中，A(1, 2, 3)，B(−2, −1, 6)，C(3, 2, 1)，D(4, 3, 0)，则直线AB与CD的位置关系是________．


已知直线l：mx+y−1=0，圆C： x2+y2=n(m，n∈R)，则直线l过定点________；若直线l与圆C恒有公共点，则n的取值范围是________.


已知圆C1：x2+y2=4与圆C2：x−22+y2=4相交，则两圆的公共弦所在直线的方程为________，公共弦的长度为________.
四、填空题

在△ABC中，已知A1,3，B5,1，且BC边的中点N在x轴上，AC边的中点M在y轴上．
(1)求三点C，M，N的坐标；

(2)求点C到直线MN的距离．

已知圆P过点A1,0 ，B4,0.
(1)若圆P还过点C6,−2，求圆P的方程；

(2)若圆心P的纵坐标为2，求圆P的方程．

如图，在直三棱柱ABC−A1B1C1中， ∠ACB=90∘，AA1=AC=BC=1.

(1)求异面直线BC1与A1B1所成角；

(2)求直线BA1与平面ABC1所成角的正弦值．

已知圆C的圆心在x轴的正半轴上，且圆C与y轴相切，点P2,4在圆C上.
(1)求圆C的方程；

(2)若直线l:m+1x+y+m+4=0与圆C交于A，B两点，|AB|=8，求实数m的值.

如图，在以A，B，C，D，E，F为顶点的多面体中，四边形ABCD是矩形， AB=2，AD=6，EA⊥平面ABCD， FD//EA，EA=12FD=2.

(1)求证： BE//平面CDF；

(2)求二面角C−EF−D的正弦值．

设M为圆N： x−12+y+22=5上的动点，PM是圆的切线且|PM|=2.
(1)求动点P的轨迹C的方程；

(2)是否存在斜率为1的直线l，满足以l被轨迹C截得的弦AB为直径的圆过原点？若存在，求出直线l的方程；若不存在，说明理由．
参考答案与试题解析
2020-2021学年福建省泉州市高二（上）10月月考数学试卷
一、选择题
1.
【答案】
B
【考点】
直线的斜率
直线的倾斜角
【解析】
l1，l2关于x轴对称，设l1, 12的斜率为k1和k2，则有k1+k2=0，又由k1=1，得k2=−1，则l2的倾斜角为3π4.
【解答】
解：l1，l2关于x轴对称，设l1, l2的斜率为k1和k2，
则有k1+k2=0，
又由k1=1，得k2=−1，
则l2的倾斜角为3π4.
故选B.
2.
【答案】
A
【考点】
两条平行直线间的距离
【解析】
此题暂无解析
【解答】
解：由平行线间的距离公式可知，
直线6x+8y−2=0与6x+8y−3=0间的距离为d=|−2+3|62+82=110．
故选A.
3.
【答案】
D
【考点】
向量加减混合运算及其几何意义
向量的三角形法则
【解析】
此题暂无解析
【解答】
解：由题意得，在三棱锥O−ABC中，点D是棱AC的中点，如图，
已知OA→=a→，OB→=b→，OC→=c→，
∴ BO→=−b→，
由图可知，BD→=BO→+OD→，
OD→=OA→+12AC→
=OA→+12OC→−12OA→
=12OA→+12OC→
=12a→+12c→，
BD→=BO→+OD→=12a→−b→+12c→.
故选D.
4.
【答案】
D
【考点】
直线与圆的位置关系
【解析】
此题暂无解析
【解答】
解：∵ ⊙A，⊙B，⊙C两两外切，它们的半径分别为2，3，10，
∴ AB=2+3=5，BC=3+10=13，AC=2+10=12，
∵ AB2+AC2=BC2，
∴ △ABC为直角三角形.
故选D．
5.
【答案】
B
【考点】
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解：|PM|的最小值就是点M到直线l：2x−y+3＝0的距离，
即|2×4−(−1)+3|22+(−1)2=1255.
故选B.
6.
【答案】
C
【考点】
三角形五心
直线的点斜式方程
两条直线垂直与倾斜角、斜率的关系
【解析】
外心是三角形三条边的垂直平分线的交点，重心是三角形三条中线的交点，垂心是三角形三条高的交点.
【解答】
解：∵B−1,0，C0,2，
∴线段BC的中点的坐标为−12,1，
线段BC所在直线的斜率kBC=2−00−(−1)=2，
则线段BC垂直平分线的斜率为−12，
线段BC垂直平分线的方程为y−1=−12(x+12)，
即2x+4y−3=0.
∵AB=AC，
∴ △ABC的外心、重心、垂心都在线段BC的垂直平分线上，
∴ △ABC的欧拉线方程为：2x+4y−3=0.
故选C.
7.
【答案】
A
【考点】
点、线、面间的距离计算
【解析】
以D为坐标原点，直线DA，DC，DD1分别为x，y，z轴，建立空间直角坐标系，利用向量法能求出点E到平面ACD1的距离．
【解答】
解：方法一：
以D为坐标原点，直线DA，DC，DD1分别为x，y，z轴建立空间直角坐标系，如图，
则D1(0, 0, 1)，A(1, 0, 0)，C(0, 2, 0)．
E为AB的中点，则E(1,1,0)，
D1E→=(1, 1, −1)，AC→=(−1, 2, 0)，AD1→=(−1, 0, 1)，
设平面ACD1的法向量为n→=(a, b, c)，
则n→⋅AC→=0，n→⋅AD1→=0， 即−a+2b=0，−a+c=0，
取a=2，得n→=(2, 1, 2)，
点E到平面ACD1的距离为：
d=|D1E→⋅n→||n→|=2+1−23=13．
方法二：
∵ 在长方体ABCD−A1B1C1D1中，AD=AA1=1，AB=2，
∴ AC=AB2+BC2=5，
AD1=AA12+A1D12=2，
CD1=CC12+C1D12=5，
∴ cs∠D1AC=2+5−52×2×5=1010，
∴ sin∠D1AC=1−110=31010，
∴ S△ACD1=12×2×5×31010=32.
∵ 点E是棱AB的中点，
∴ S△ACE=12×1×1=12.
设E到平面ACD1的距离为d，
由VE−ACD1=VD1−ACE可得：
13×32×d=13×12×1，
∴ d=13．
故选A.
8.
【答案】
A
【考点】
二倍角的余弦公式
余弦定理
直线与圆的位置关系
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解：设圆C：x2+y2−2x=0，化为标准方程为(x−1)2+y2=1，
圆心C(1,0)，r=1，如图，
要使|MN|的长度最小，则∠MCN最小，即∠MCP最小.
因为tan∠MCP=|PM|r=|PM|，所以当|PM|最小时，|MN|最小.
又因为|PM|=|PC|2−1，所以当|PC|最小时，|MN|最小.
因为|PC|min=41+1=22，
所以cs∠MCP=122=24，
cs∠MCN=2cs2∠MCP−1=−34，
则|MN|min=12+12−2×1×1×−34=142，
当点P在直线x−y+3=0无限远取值时，∠MCN→180∘，|MN|→直径2，
所以142≤|MN|0，
由圆C与y轴相切，得半径r=a，
由点P在圆上，得|PC|=r，即(a−2)2+(0−4)2=a2，
解得a=5，
所以圆C的方程为(x−5)2+y2=25.
(2)由(1)得圆心C(5,0)，半径r=5，
所以圆心C到直线l的距离d=|5(m+1)+m+4|(m+1)2+1=|6m+9|(m+1)2+1，
由弦长|AB|=2r2−d2=225−d2=8，得d2=9，即d=3，
由|6m+9|(m+1)2+1=3，得m=−73或−1，都符合题意，
所以m的值为−73或−1.
【考点】
直线与圆的位置关系
直线与圆相交的性质
圆的标准方程
点到直线的距离公式
【解析】
此题暂无解析
【解答】
解：(1)由题意设圆心C(a,0)，a>0，
由圆C与y轴相切，得半径r=a，
由点P在圆上，得|PC|=r，即(a−2)2+(0−4)2=a2，
解得a=5，
所以圆C的方程为(x−5)2+y2=25.
(2)由(1)得圆心C(5,0)，半径r=5，
所以圆心C到直线l的距离d=|5(m+1)+m+4|(m+1)2+1=|6m+9|(m+1)2+1，
由弦长|AB|=2r2−d2=225−d2=8，得d2=9，即d=3，
由|6m+9|(m+1)2+1=3，得m=−73或−1，都符合题意，
所以m的值为−73或−1.
【答案】
解：(1)由已知得EA⊥AB，EA⊥AD，AB⊥AD，
以A为坐标原点，分别以AB，AD，AE为x，y，z轴建立空间直角坐标系，如图，
B(2,0,0)，E(0,0,2)，BE→＝(−2,0,2)，
A(0,0,0)，D(0,6,0)，AD→=(0,6,0)，
易得平面CDF的一个法向量为AD→=(0,6,0)，
由BE→⋅AD→=0得BE→⊥AD→，
所以BE//平面CDF.
(2)C(2,6,0)，E(0,0,2)，F(0,6,22)，D(0,6,0)，
易得平面DEF的一个法向量为m→=(1,0,0)，
设平面CEF的一个法向量为n→=(x,y,z)，
EF→=(0,6,2)，CF→=(−2,0,22)，
由n→⊥EF→，n→⊥CF→，得 n→⋅EF→=6y+2z=0，n→⋅CF→=−2x+22z=0，
即3y+z=0，−x+2z=0，
取z=3，得y=−1，x=6，所以n→=(6,−1,3)，
设二面角C−EF−D的大小为θ，
则csθ=|cs|=n→⋅m→|n|→⋅|m|→=610×1=155，
sinθ=1−cs2θ=105，
所以二面角C−EF−D的正弦值为105.
【考点】
用空间向量求平面间的夹角
直线与平面平行的判定
【解析】
此题暂无解析
【解答】
解：(1)由已知得EA⊥AB，EA⊥AD，AB⊥AD，
以A为坐标原点，分别以AB，AD，AE为x，y，z轴建立空间直角坐标系，如图，
B(2,0,0)，E(0,0,2)，BE→＝(−2,0,2)，
A(0,0,0)，D(0,6,0)，AD→=(0,6,0)，
易得平面CDF的一个法向量为AD→=(0,6,0)，
由BE→⋅AD→=0得BE→⊥AD→，
所以BE//平面CDF.
(2)C(2,6,0)，E(0,0,2)，F(0,6,22)，D(0,6,0)，
易得平面DEF的一个法向量为m→=(1,0,0)，
设平面CEF的一个法向量为n→=(x,y,z)，
EF→=(0,6,2)，CF→=(−2,0,22)，
由n→⊥EF→，n→⊥CF→，得 n→⋅EF→=6y+2z=0，n→⋅CF→=−2x+22z=0，
即3y+z=0，−x+2z=0，
取z=3，得y=−1，x=6，所以n→=(6,−1,3)，
设二面角C−EF−D的大小为θ，
则csθ=|cs|=n→⋅m→|n|→⋅|m|→=610×1=155，
sinθ=1−cs2θ=105，
所以二面角C−EF−D的正弦值为105.
【答案】
解：(1)由已知得圆心N1,−2，半径|MN|=r=5 ，
则|PN|=|MN|2+|PM|2=3 ，
所以动点P到定点N的距离都等于3，
则动点P的轨迹C是以N为圆心，3为半径的圆，
所以轨迹C的方程为x−12+y+22=9.
(2)假设存在斜率为1的直线l，满足题意，
设Ax1,y1，Bx2,y2，直线l的方程为y=x+b，
圆C的标准方程为x−12+y+22=9，
即x2+y2−2x+4y−4=0，
由y=x+b，x2+y2−2x+4y−4=0，
消去y得2x2+2b+1x+b2+4b−4=0 ，
则此方程两根为x1，x2，
且x1+x2=−b+1，x1⋅x2=b2+4b−42 ，
以AB为直径的圆过原点O，则OA⊥OB ，
即kOA⋅kOB=y1x1⋅y2x2=−1，x1x2+y1y2=0 ，
又y1=x1+b，y2=x2+b，
所以x1x2+x1+bx2+b=0，
即2x1x2+bx1+x2+b2=0，
所以b2+3b−4=0，
解得b=−4或b=1，
Δ=2b+22−8b2+4b−4=−4b2+6b−9，
经检验当b=−4或b=1时满足Δ>0，
所以存在这样的直线l为y=x−4或y=x+1，
即x−y−4=0或x−y+1=0.
【考点】
直线和圆的方程的应用
轨迹方程
【解析】

【解答】
解：(1)由已知得圆心N1,−2，半径|MN|=r=5 ，
则|PN|=|MN|2+|PM|2=3 ，
所以动点P到定点N的距离都等于3，
则动点P的轨迹C是以N为圆心，3为半径的圆，
所以轨迹C的方程为x−12+y+22=9.
(2)假设存在斜率为1的直线l，满足题意，
设Ax1,y1，Bx2,y2，直线l的方程为y=x+b，
圆C的标准方程为x−12+y+22=9，
即x2+y2−2x+4y−4=0，
由y=x+b，x2+y2−2x+4y−4=0，
消去y得2x2+2b+1x+b2+4b−4=0 ，
则此方程两根为x1，x2，
且x1+x2=−b+1，x1⋅x2=b2+4b−42 ，
以AB为直径的圆过原点O，则OA⊥OB ，
即kOA⋅kOB=y1x1⋅y2x2=−1，x1x2+y1y2=0 ，
又y1=x1+b，y2=x2+b，
所以x1x2+x1+bx2+b=0，
即2x1x2+bx1+x2+b2=0，
所以b2+3b−4=0，
解得b=−4或b=1，
Δ=2b+22−8b2+4b−4=−4b2+6b−9，
经检验当b=−4或b=1时满足Δ>0，
所以存在这样的直线l为y=x−4或y=x+1，
即x−y−4=0或x−y+1=0.