人教版八年级上册14.2.1 平方差公式教案配套课件ppt

这是一份人教版八年级上册14.2.1 平方差公式教案配套课件ppt，共22页。PPT课件主要包含了学习目标，重点难点，复习备用，多项式的乘法法则，am+an，bm+bn，m+n，a+b，新知探究，x2-1等内容，欢迎下载使用。
第十四章 整式的乘法与因式分解
14.2 乘法公式
2.1 平方差公式
1.知道平方差公式，能用几何拼图的方式验证平方差公式，能灵活应用平方差公式进行计算2.经历通过观察、计算、猜想得出平方差公式，并运用几何拼图验证平方差公式的过程，体会数形结合的思想.
重点:平方差公式的探究及应用.难点:灵活运用平方差公式进行计算.
用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加.
探究：计算下列多项式的积，你能发现什么规律?(1)(x+1)(x﹣1)= ；(2)(m+2)(m﹣2)= ；(3)(2x+1)(2x﹣1)= .
这几个运算都是形如a+b的多项式与形如a -b的多项式相乘.
(a+b)(a-b)＝a2-ab+ab-b2
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积等于这两个数的平方差.
(a+b)(a-b) = a 2 - b 2
平方差公式与多项式乘法对比：(a+b)(p+q)，p=a，q=﹣b的特殊情形.
(b+a)(-b+a)=a2-b2
(-a+b)(-a-b)=(-a)2-b2
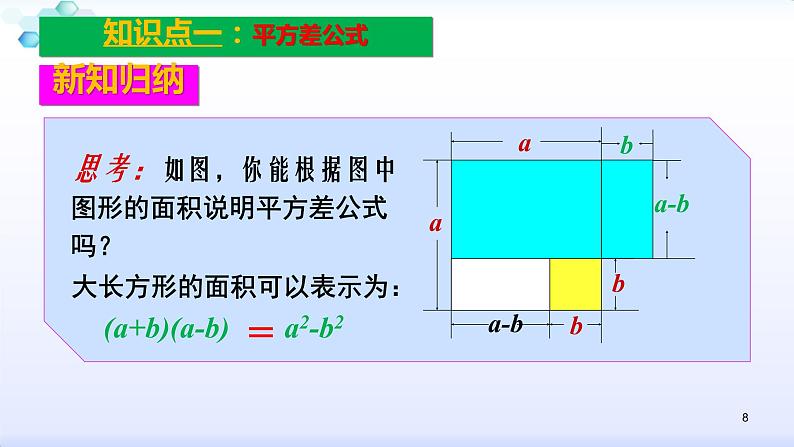
思考：如图，你能根据图中图形的面积说明平方差公式吗？
大长方形的面积可以表示为：
例1：用平方差公式计算(1) (3x+2)(3x-2) ；(2) (b+2a)(2a﹣b); (3) (-x+2y)(-x-2y).
(a+b)(a -b)
找符号相同项与符号相反项，相同为a ，相反为b，结果为：相同项2-相反项2
先独立完成导学案互动探究1、2，再同桌相互交流，最后小组交流；
(1)平方差公式中的字母a，b可以是单项式，也可以是多项式，只要符合这个公式的结构特征就可以运用这个公式.(2)在运用公式时，要分清哪个相当于公式中的a，哪个相当于公式中的b，不要混淆.
（1）(2+a)(a−2) （2）(−4k+3)(−4k−3) （3）(1−x)(−x−1)（4）(−x−1)(x+1)（5）(x+3)(x−2)（6）(a+b+c)(a+b−c)
1、下列式子可以用平方差公式计算吗？
2.计算(1-m)(-m-1)，结果正确的是( )A.m2-2m-1 B.m2-1 C.1-m D.m2-2m+13.三个连续整数，中间的一个是n，则这三个整数的积是( )A .3n B.n3 C.n3-1 D.n3-n 4.若x+y＝6，x-y＝5，则x2-y2的值是 .5.若计算(x+m)(x+ )的结果不含字母x的一次项，则 (x+m)(x-m)＝ .
6.观察下列各式:1×3＝22-1，3×5＝42-1，5×7＝62-1，7×9＝82-1，…把发现的规律用含字母n(n为正整数)的等式表示为 .
(2n-1)(2n+1)＝4n2-1
平方差公式的变化及应用
(4)指数变化 (a2+b2)(a2-b2)=(a2)2-(b2)2=a4-b4
(1)位置变化 (b+a)(-b+a)=(a+b)(a-b)=a2-b2
(2)符号变化 (-a-b)(a-b)=(-b-a)(-b+a)=(-b)2-a2=b2-a2
(3)系数变化 (3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2
(6)连用公式变化 (a+b)(a-b)(a2+b2)＝(a2-b2)(a2+b2)＝a4-b4
(5)增项变化 (a-b+c)(a-b-c)=(a-b)2-c2
例2： 简化计算:(1) (y+2) (y-2) – (y-1) (y+5); (2) 102×98 .
知识点二：平方差公式的应用
(2) 原式=(100＋2)(100－2)
=10000 – 4
解:(1) 原式= (y2-22)-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
先独立完成导学案互动探究3，再同桌相互交流，最后小组交流；
1.计算 20192 － 2020×2018;
= 20192－ (2019+1)(2019-1)
= 20192－ 20192+12
= 20192－ (20192－12 )
2.化简(x+y+z)2ー(x+yー2)2的结果是( )A. 4yz B .8xy C .4yz+4xz D .8xz3.阅读理解:引人新数i，新数i满足分配律、结合律交换律.已知i2＝-1，那么(1+2i)・(1-2i)＝ .4.如果(2a+2b-3)(2a+2b+3)＝40，那么a+b＝ .5.已知xーy＝2，yーz＝2，z+x＝2，则x2-z2的值是 ×997= .
对自己说，你有什么收获？ 对同学说，你有什么温馨提示？ 对老师说，你还有什么困惑？