




数学八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称复习ppt课件
展开1.能说出轴对称图形、轴对称的概念及性质.2.能按要求作出简单平面图形经过一次或两次轴对称后的图形,能指出对称轴.3.能用尺规作图作出线段的垂直平分线,能利用垂直平分线的性质解决问题.4.能说出等腰(等边)三角形的性质和判定,并能熟练应用,解决问题.
重点:轴对称、等腰三角形的性质和判定.难点:轴对称的性质、等腰三角形的性质和判定的应用.
知识点一:轴对称图形的识别
把一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称.
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.
轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线
①一个具有特珠形状的图形
两个图形的特殊位置关系
②对称点在同一个图形上
对称点分别在两个图形上
③不一定只有一条对称轴
④对称轴是过图形的某条直线
(1)沿对称轴折叠,图形的两部分重合;(2)把成轴对称的两个图形看成一个整体,它就是一个轴对称图形;把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线成轴对称.
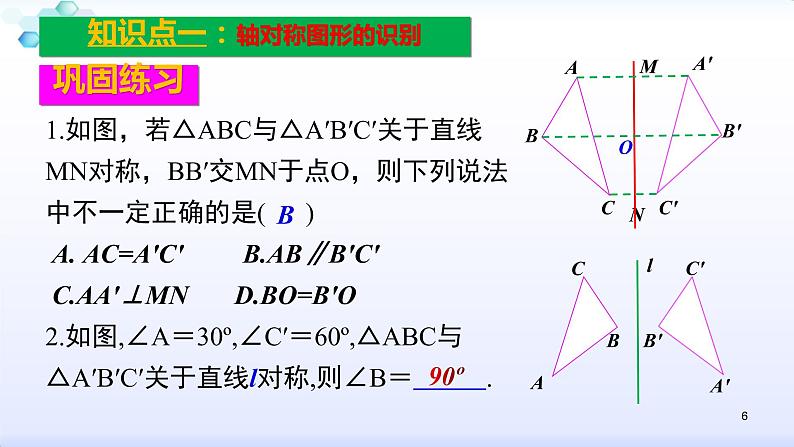
1.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( ) A. AC=A'C' B.AB∥B′C′ C.AA′⊥MN D.BO=B′O2.如图,∠A=30º,∠C′=60º,△ABC与△A′B′C′关于直线l对称,则∠B= .
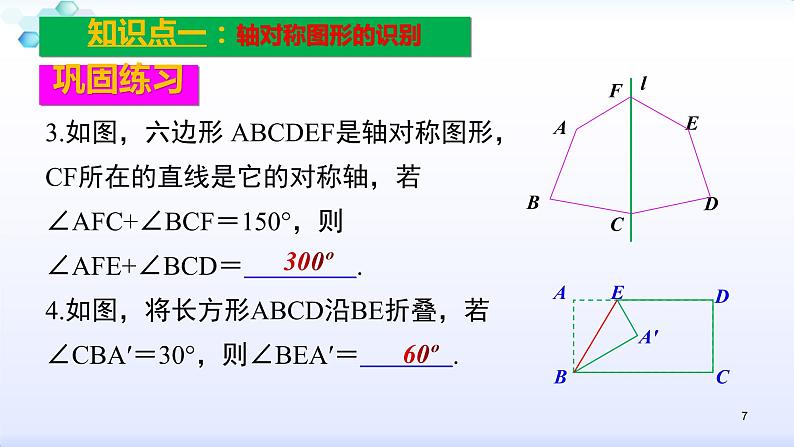
3.如图,六边形 ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD= .4.如图,将长方形ABCD沿BE折叠,若∠CBA′=30°,则∠BEA′= .
先独立完成导学案专题一,再同桌相互交流,最后小组交流;
知识点二:画轴对称图形
画特殊点关于直线的对称点
作垂直、截等线、顺次连.
1.如图,△ABC和△A′B′C′关于直线MN对称,其中点A,A′是一组对称点,若AA′=3cm,则AA′ MN,且A′O= =1.5cm.
2、如图,画出下列图形并作出下列图形关于直线l 对称的图形.
折叠也是一种轴对称,折叠前后的两个图形是全等形,折痕所在的直线是对称轴,它们的对应角、对应边相等.
1.将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是( )
2、如图,在2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.在网格中与△ABC成轴对称的格点三角形一共有 个.
3、如图,方格纸上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,最多能画 条线段.
点(x,y)关于x 轴对称的点的坐标为(__ ,__); 点(x,y)关于y 轴对称的点的坐标为(__ ,__).
x -y
- x y
横轴对称横不变,纵轴对称纵不变。
例1:如图,四边形ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4), 分别画出与四边形ABCD 关于x 轴和y 轴对称的图形.
画轴对称图形的步骤:①找、②画、③连
画出与一个图形关于x轴或y轴对称的图形问题 只要先求出已知图形中的一些特殊点(如多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形关于坐标轴对称的图形.
1.如图,已知三个点A(-4,1),B(-2,-1),C(-1,3)(1)作出与△ABC关于y轴对称的△A′B′C′;(2)写出△A′B′C′的三个顶点的坐标.
2.已知点A(m+2,3)和B(-5,n+6)关于y轴对称,则m= , n= .3.已知两点A(x1,y1),B(x2,y2),如果x1+x2=0,y1-y2=0,那么点A和点B关于 对称.
4.如图,△ABC关于直线 y=1对称,点C到AB的距离为2,AB的长为6,则点A,B的坐标分别为 .
先独立完成导学案专题二,再同桌相互交流,最后小组交流;
知识点三:线段垂直平分线
∵PC⊥AB,AC=CB∴PA=PB
线段的垂直平分线的性质: 线段垂直平分线上的点与这条线段两个端点的距离相等.
②∵PA=PB,AC=CB∴PC⊥AB.
线段垂直平分线的判定: 与线段两个端点的距离相等的点在这条线段的垂直平分线上.
③∵PA=PB,PC⊥AB∴AC=CB.
①∵PA=PB,∴或点P在线段AB的垂直平分线上.
例2:尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和直线AB外一点C(如图).求作:AB的垂线,使它经过点C.
例3:如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A′′B′′C′′关于直线EF对称.(1)画出直线EF;(2)直线MN与EF相交于点O,试探究直线MN,EF所夹锐角α与∠BOB′′的数量关系.
(1)作对称轴的依据: 如果一个图形是轴对称图形或两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线;
(2)作对称轴的步骤:①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;②连:连接这对对应点;③作:作出对应点所连线段的垂直平分线这条垂直平分线就是该轴对称图形或成轴对称的两个图形的对称轴.
1.如图,在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠ACB=80°,则∠BCE的度数为 .2.如图,已知△ABC中,AB=5cm,AC=3cm,BC=5cm,l是边BC的垂直平分线,与AB交于点D,与BC交于点E,则△ACD的周长是 .
3.如图,AB=AD,BC=DC,则有( )A.BD垂直平分AC B.AC垂直平分BDC.BD平分∠ABC D.∠BAC=∠BDC
4.如图,在∆ABC中,已知点D在BC上,且BD+AD=BC, 求证:点D在AC的垂直平分线上.
5.如图,已知两条公路AO,BO交于点O,有两个村庄M,N,要修建一座仓库,使仓库到两条公路的距离相等,并且到两个村庄的距离相等,试在图中找到位置并标出.
先独立完成导学案专题三,再同桌相互交流,最后小组交流;
知识点四:等腰三角形的性质与判定
性质1 等腰三角形的两个底角相等(简写成“等边对等角”);
在△ABC中∵ AB=AC∴ ∠B=∠C
性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。(可简记为“三线合一”)
①∵AB =AC,∠1 =∠2∴BD=CD,AD⊥BC.
②∵AB =AC,BD=CD.∴∠1 =∠2,AD⊥BC.
③∵AB =AC,AD⊥BC∴∠1 =∠2,BD=CD.
1 、 等腰三角形两腰上的中线相等、两腰上的高相等、两个底角的平分线也相等;
2 、等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.
3、 等腰三角形底边上的高(中线或顶角平分线)上任意一点到两腰的距离相等,到两底角顶点的距离相等;
4 、 若等腰三角形的顶角为90°,则此三角形为等腰直角三角形,其两个底角均为45°.
1.如图,已知∠ACB=90°,BD=BC,AE=AC,则∠DCE的度数是 .2.如果等腰三角形一腰上的高与另一腰的夹角是20°,那么该三角形的一个底角为 .
3.△ABC中点D在BC边上,BD=AD=AC,E为CD的中点若∠CAE=16°,则∠B为 度.4.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,求证:BE=CE
证明:∵AB=AC,点D是BC的中点,∴AD⊥BC,∴AD垂直平分BC,∴BE=CE
定义:由两边相等的三角形是等腰三角形
定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
∵ AB=AC,∴△ABC是等腰三角形
∵ ∠B=∠C ∴ AB=AC
1.在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,交AC于点D,则该图中共有等腰三角形( ) A.1个 B.2个 C.3个 D.4个2.如图,在△ABC中AB=AC,∠ABC=36°,点D,E是BC上两点,且∠1=∠2=∠3,则图中等腰三角形有( )A.4个 B.5个 C6个 D.7个
3.如图,在∆ABC中,且BA=BC,点D是AB延长线上一点,DF⊥ AC于F,交BC于E,求证:∆DBE是等腰三角形.
先独立完成导学案专题四,再同桌相互交流,最后小组交流;
知识点五:等边三角形的性质与判定
等边三角形的三个内角都相等,并且每一个内角都等于60°.
∵ ∆ABC是等边三角形,∴ ∠A=∠B=∠C=60°
等边三角形具有等腰三角形所有的性质
等边三角形一定是等腰三角形,等腰三角形不一定是等边三角形.
1.如图,△ABC是等边三角形,点D在AC边上,∠DBC=35°,则∠ADB的度数为( )A.25°B.60°C.85°D.95°2.如图,一张等边三角形纸片,剪去一个角后得到一个四边形,则图中α+β的度数是( )A.180°B.220°C.240°D.300°
3等边三角形的两条高线相交所成钝角的度数是( )A.105°B.120°C.135°D.150°4.如图,△ABC为等边三角形,AD⊥BC,AE=AD,则∠ADE= .
1、三条边都相等的三角形是等边三角形(定义)
2、三个角都相等的三角形是等边三角形
3、有一个角是60°的等腰三角形是等边三角形
∵ AB=AC,∠B=60°∴ ∆ABC是等边三角形
1.如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD,求证:△OCD是等边三角形.
2.如图,已知△ABC和△BDE均为等边三角形,连接AD,CE,若∠BAD=39°,则∠BCE= 度.3.如图,等边三角形ABC和等边三角形BDE,且点E在线段AD上.求证:BD+CD=AD
含30°的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在Rt∆ABC中∠C=90°,∠A=30°∴ BC= AB
1.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则BD的长是( ).A. 3 cm B. 6 cm C. 9 cm D. 12 cm2.如图,在Rt△ABC中,∠ACB=90°,∠B=15°,AB边的垂直平分线交AB于点E,交BC于点D,且BD=18cm,则AC的长是 .
3.如图所示,点P是∠AOB平分线上的一点,过点P作PC∥OA交OB于点C,若∠AOB=30°,OC=4,求点P到OA的距离PD.
解题时,一般是先寻找30°角所在的直角三角形,得到斜边与直角边的关系,当30°角不在一个直角三角形中时,可考虑作垂线得到含30°角的直角三角形,或作等腰三角形构造顶角的邻补角为60°.当三角形中含15°,30°,60°,120°角时,也可通过添加辅助线,构造含30°角的直角三角形求解.
利用含30°角的直角三角形的性质解决问题的方法
先独立完成导学案专题五,再同桌相互交流,最后小组交流;
对自己说,你有什么收获? 对同学说,你有什么温馨提示? 对老师说,你还有什么困惑?
2020-2021学年第十三章 轴对称综合与测试复习ppt课件: 这是一份2020-2021学年第十三章 轴对称综合与测试复习ppt课件,共46页。PPT课件主要包含了本章知识回顾,轴对称的性质,观察与思考,练一练,大显身手等内容,欢迎下载使用。
2020-2021学年13.1.1 轴对称图片ppt课件: 这是一份2020-2021学年13.1.1 轴对称图片ppt课件,共25页。PPT课件主要包含了做一做,概念辨析,APPA’等内容,欢迎下载使用。
初中13.1.1 轴对称教学演示ppt课件: 这是一份初中13.1.1 轴对称教学演示ppt课件,共28页。PPT课件主要包含了学习目标,重点难点,画轴对称图形,找特殊点如顶点,顺次连接所画的对称点,复习备用,新知探究,-1-2,规律发现,学以致用等内容,欢迎下载使用。













