2020-2021学年3 边角边备课ppt课件

这是一份2020-2021学年3 边角边备课ppt课件，共26页。PPT课件主要包含了学习目标，重点难点，复习备用，全等三角形的判定，书写步骤，2三条边，1三个角，3两边一角，4两角一边，SSS等内容，欢迎下载使用。

1.经历三角形全等的判定方法“边角边”的探索过程.2.知道不能用“边边角”来判定两个三角形全等.3.会应用“边角边”判定三角形全等，并能进行简单的推理.
重点:运用"边角边”判定两个三角形全等.难点:三角形的全等判定方法“边角边”的探索.
方法1：边边边 (SSS)
尺规作图：作一个角等于已知角
1、准备条件：证全等时要用的间接条件要先证好；
2、三角形全等书写三步骤：
①写出在哪两个三角形中；
②摆出三个条件用大括号括起来；
除了SSS外,还有其他情况吗？继续探索三角形全等的条件.
当两个三角形满足六个条件中的三个时，有四种情况:
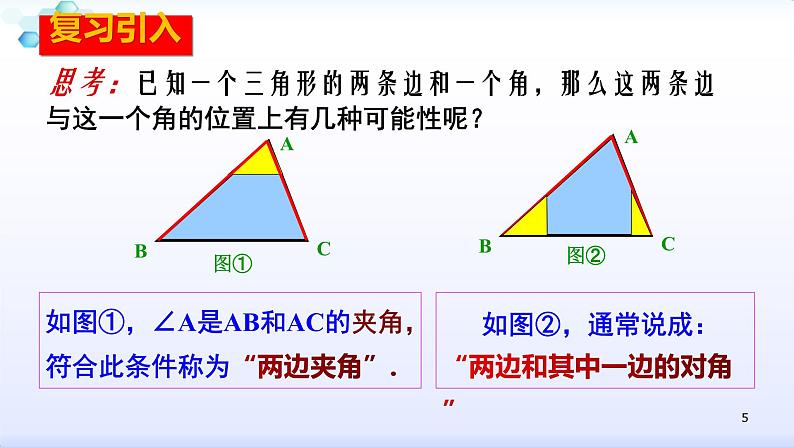
思考：已知一个三角形的两条边和一个角，那么这两条边与这一个角的位置上有几种可能性呢？
如图①，∠A是AB和AC的夹角，符合此条件称为“两边夹角”.
如图②，通常说成：“两边和其中一边的对角”
大家知道，两个三角形仅有两个元素分别相等，这两个三角形不一定会全等;而三边分别相等的两个三角形一定全等.那么，这节课我们一起来探索两边及一角分别相等的情形:1.两边和它们的夹角分别相等的两个三角形会全等吗?2.两边和其中一边的对角分别相等的两个三角形会全等吗?
知识点一：全等三角形的判定方法2：“SAS”
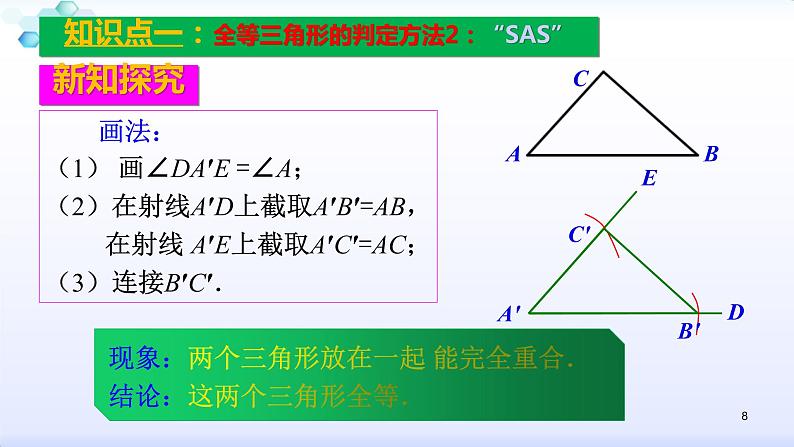
探究 3： 先任意画出一个∆ABC.再画一个∆A'B'C',使A'B'=AB, A'C'=AC，∠A'=∠A.(即两边和它们的夹角分别相等)把画好的△A'B'C'剪下来，放到∆ABC上，它们全等吗?
1.两边和它们的夹角分别相等的两个三角形会全等吗?
现象：两个三角形放在一起 能完全重合．结论：这两个三角形全等．
　　画法：（1） 画∠DA′E =∠A；（2）在射线A′D上截取A′B′=AB， 在射线 A′E上截取A′C′=AC；（3）连接B′C′．
三角形全等判定方法2
　两边和它们的夹角对应相等的两个三角形全等。 简写为“边角边”或“SAS”
在 ∆ABC 和 ∆DEF 中，∴　 ∆ABC ≌ ∆DEF (SAS).
例1：如图，有一池塘，要测池塘两A.端A，B的距离，可先在平地上取一个点C，从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE，那么量出DE的长就是A，B的距离，为什么?
∴∆ABC≌∆DEC
CA = CD，∠1 = ∠2，
解：在△ABC和△DEC中
∴AB=DE ( )
因为全等三角形的对应边相等，对应角相等，所以证明线段相等或者角相等时，常常通过证明它们是全等三角形的对应边或对应角来解决.
1：如图，CA=CE，∠1=∠2，CB=CD,求证：△ABC≌△EDC .
证明:∵ ∠1=∠2， ∴∠1+∠ACE=∠2+∠ACE，即 ∠ACB=∠ECD
在△ABC和△EDC中
∴ △ABC ≌△EDC（SAS）.
2.如图，在四边形ABCD中 AB=CD，AB∥CD，求证：∠B=∠D .
在△ABC和△CDA中
∴ △ABC ≌△CDA（SSS），
∴ ∠B=∠D（ ）.
证明:∵ AB∥CD， ∴∠1=∠2，
求证：AD∥CB .
3.如图，点A,F,C,D在同一条直线上，AF=DC，AB=DE，AB∥DE.求证：∠B=∠D .
4.如图，点A,F,C,D在同一条直线上，AF=DC，AB=DE，AB∥DE.求证：∠CBF=∠FEC .
5.如图，点A,F,C,D在同一条直线上，AF=DC，AB=DE，AB∥DE.求证：∠ADB=∠DAE .
先独立完成导学案互动探究1、2、3，再同桌相互交流，最后小组交流；
两边夹角边角边，边角顺序不能变. 隐含条件要挖掘，恰如其分来分辨.
知识点二：“SSA”不能判定两个三角形全等
思考？： 如图，把一长一短的两根木棍的一端固定在一起，摆出△ABC.固定住长木棍，转动短木棍，得到△ABD.这个实验说明了什么?
结论： 两边和其中一边的对角分别相等的两个三角形不一定全等 .
　　如图，在△ABC 和△ABD 中， AB =AB，AC = AD，∠B =∠B，但△ABC 和△ABD 不全等．　
1.如图，点B,F,C,E在同一条直线上，点A,D在直线BE的两侧,AB// DE,BF=CE,请添加一个适当的条件: ,使得△ABC 和△DEF 全等.
AB=DE
先独立完成导学案互动探究4，再同桌相互交流，最后小组交流；
方法2：边角边 (SAS)
两边和其中一边的对角分别相等的两个三角形不一定全等
对自己说，你有什么收获？ 对同学说，你有什么温馨提示？ 对老师说，你还有什么困惑？