高中苏教版2.2.2 函数的奇偶性教案及反思

这是一份高中苏教版2.2.2 函数的奇偶性教案及反思，共4页。教案主要包含了教材分析，学情分析，教学重难点，教学目标，教学过程等内容，欢迎下载使用。

本节课选自苏教版高中数学必修1第二章；教材通过对具体函数的图像及函数值对应表归纳和抽象，概括出了函数奇偶性的准确定义。然后，为深化对概念的理解。函数的奇偶性是函数的重要性质，是对函数概念的深化。它把自变量取相反数时函数值间的关系定量地联系在一起，反映在图像上形成对称性。这样，就从数、形两个角度对函数的奇偶性进行了定量和定性的分析。它的研究也为今后幂函数、三角函数的性质等后续内容的深入起着铺垫的作用。
二、学情分析
学生已经学习了函数的单调性，对于研究函数的性质的方法已经有了一定的了解。尽管他们尚不知函数奇偶性,但学生在初中已经学习过图形的轴对称与中心对称，对图象的特殊对称性早已有一定的感性认识；在研究函数的单调性方面，学生懂得了由形象到具体,然后再由具体到一般的科学处理方法,具备一定数学研究方法的感性认识；高一学生具备一定的观察能力，但观察的深刻性及稳定性也都还有待提高；
三、教学重难点
重点：函数奇偶性概念和函数奇偶性的判断。
难点：函数奇偶性概念的形成。
四、教学目标
知识与技能目标：表述函数奇偶性的概念；能利用定义判断函数的奇偶性
过程与方法目标：通过体验函数奇偶性概念的形成过程体会到了数形结合的思想方法，感悟由形象到具体,再从具体到一般的研究方法。
情感态度与价值观目标：体验数学研究严谨性，感受数学对称美。
五、教学过程
（一）情境导航、引入新课
这些图片源于生活，很显然都具有对称性，那么我们现在正在学习的函数图象，是否也会具有对称的特性呢？是否也体现了图象对称的美感呢？
设计意图：体会数学来源于生活，提高学生学习的积极性
（二）构建概念、突破难点
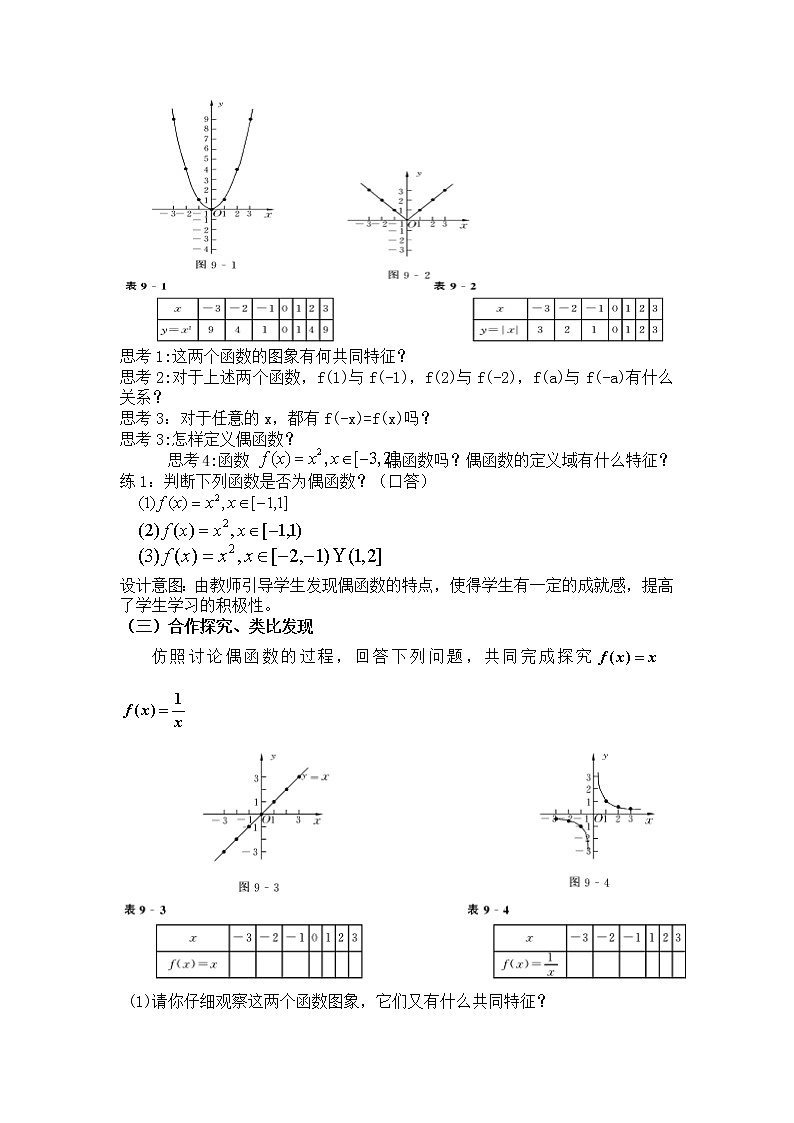
考察下列两个函数：(1) (2)
思考1:这两个函数的图象有何共同特征？
思考2:对于上述两个函数，f(1)与f(-1)，f(2)与f(-2)，f(a)与f(-a)有什么关系？
思考3：对于任意的x，都有f(-x)=f(x)吗？
思考3:怎样定义偶函数？
思考4:函数 偶函数吗？偶函数的定义域有什么特征？
练1：判断下列函数是否为偶函数？（口答）

设计意图：由教师引导学生发现偶函数的特点，使得学生有一定的成就感，提高了学生学习的积极性。
（三）合作探究、类比发现
仿照讨论偶函数的过程，回答下列问题，共同完成探究
(1)请你仔细观察这两个函数图象，它们又有什么共同特征？
(2)请你完成下列函数值对应表，描述它们又是如何体现这些特征的呢？
(3)你能尝试利用数学语言描述函数图象的这个特征吗？
(4)对于任意的x，都有f(-x)=f(x)吗？
奇函数的定义
练2：判断下列函数是否为奇函数？（口答）
设计意图：通过学生自己合作探究，类比发现了奇函数的相关知识，加深了学生对于知识的认知程度，并且培养了学生的合作交流意识
（四）强化定义，深化内涵
对奇函数、偶函数定义的说明:
（1）如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x) 具有奇偶性。
(2)函数具有奇偶性的前提是：定义域关于原点对称。
(3)若f(x)为奇函数,则f(-x)=－f(x)成立。若f(x)为偶函数,则f(-x)=f(x)成立。
设计意图：使得学生能够认识到奇偶性间的联系和区别。
（五）讲练结合，巩固新知
例1. 利用定义判断下列函数的奇偶性
（1）
小结：用定义判断函数奇偶性的步骤:
（1）先求定义域，看是否关于原点对称；
（2）再判断f(－x)与f(x)的关系；
(3)若f(-x)=f(x)则f(x)是偶函数；若f(-x)= - f(x)则f(x)是奇函数.
练习2.利用定义判断下列函数的奇偶性
总结：根据奇偶性函数可划分为四类:
奇偶函数图象的性质:
（1）奇函数的图象关于原点对称；反过来,如果一个函数的图象关于原点对称,那么这个函数为奇函数.
（2）偶函数的图象关于y轴对称；反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.
注：奇偶函数图象的性质可用于：①判断函数的奇偶性；②简化函数图象的画法。
例2.已知函数y=f(x)是偶函数，它在y轴右边的图象如下图，画出在y轴左边的图象
x
y
0
解：
相等en等
（六）拓展迁移，能力提高
例3. 利用定义判断下列函数的奇偶性
（1）
（2）
（七）课时小结，知识建构
判断或证明函数奇偶性的基本步骤：
一看——二找——三判断
注意：若可以作出函数图象的，直接观察图象是否关于y轴对称或者关于原点对称。
（八）布置作业，回归拓展
必做题：教材第40页练习第1题
选做题：教材第43页，第6题；
奇偶性
奇函数
偶函数
定
义
设函数y=f(x)的定义域为D，任意 x属于D ,都有-x属于D .
f(-x)=-f(x)
f(-x)=f(x)
图像
性质
关于原点对称
关于y轴对称
判断
步骤
定义域是否关于原点对称.
f(-x)=-f(x)
f(-x)=f(x)