苏教版必修12.2.1 函数的单调性教案设计
展开
这是一份苏教版必修12.2.1 函数的单调性教案设计,共3页。教案主要包含了学习目标,学习重,知识要点,基础训练,例题分析等内容,欢迎下载使用。
熟练的运用判断、证明函数单调性的各种方法;
掌握集中常用的判断函数单调性的判断方法;
会运用函数的单调性解决一些数学问题。
二、学习重、难点:判断证明函数的单调性,及单调性的应用。
三、知识要点:
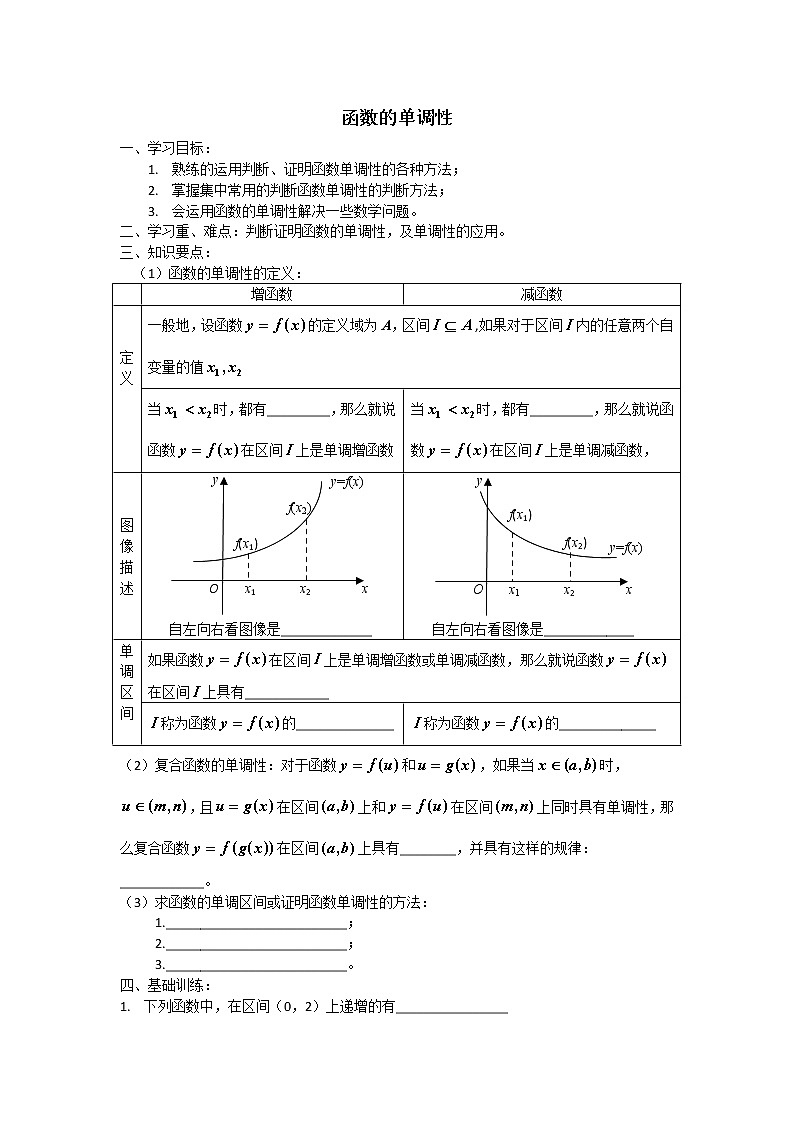
(1)函数的单调性的定义:
(2)复合函数的单调性:对于函数和,如果当时,,且在区间上和在区间上同时具有单调性,那么复合函数在区间上具有________,并具有这样的规律:____________。
(3)求函数的单调区间或证明函数单调性的方法:
1.__________________________;
2.__________________________;
3.__________________________。
四、基础训练:
下列函数中,在区间(0,2)上递增的有________________
(1) (2) (3) (4) (5)
函数的单调减区间为______________。
已知在区间上是减函数,则的取值范围是_____。
函数定义在上的减函数,则的解集为__________。
五、例题分析:
例1.判断并证明函数在上的单调性。
变式1.讨论函数的单调性。
变式2. 已知在区间上为减函数,求实数的取值范围。
例2.已知函数,求满足不等式的的取值范围。
变式:已知满足对任意x1≠x2,都有eq \f(f(x1)-f(x2),x1-x2)>0成立,求实数的取值范围。
拓展练习:
1.若f (x)=-x2+2ax与g(x)=eq \f(a,x+1)在区间[1,2]上都是减函数,则实数a的取值范围是______。
2.已知函数f (x)=x3-2x+ex-eq \f(1,ex) 满足f (2a2)≤f(1-a),则实数a的取值范围是__________。增函数
减函数
定义
一般地,设函数的定义域为A,区间,如果对于区间内的任意两个自变量的值
x
y
O
x1
x2
f(x2)
f(x1)
y=f(x)
当时,都有_________,那么就说函数在区间上是单调增函数
x
y
O
x1
x2
f(x2)
f(x1)
y=f(x)
当时,都有_________,那么就说函数在区间上是单调减函数,
图像描述
自左向右看图像是_____________
自左向右看图像是_____________
单调区间
如果函数在区间上是单调增函数或单调减函数,那么就说函数在区间上具有____________
称为函数的______________
称为函数的______________
相关教案
这是一份高中数学苏教版必修12.2.1 函数的单调性教学设计,共3页。
这是一份2021学年2.2.1 函数的单调性教案,共4页。教案主要包含了课后作业,课堂反思等内容,欢迎下载使用。
这是一份高中数学苏教版必修12.2.1 函数的单调性教学设计,共5页。教案主要包含了新课讲解,分段函数,分式函数,抽象函数等内容,欢迎下载使用。










