

高中数学苏教版必修13.2.1 对数教学设计
展开教学目标:
1.从对数发生的历史出发让学生认识到引入对数的必要性,让学生已有认知的基础上了解对数的意义,并经历对数概念的形成过程;
2.帮助学生理解对数的概念,引导学生认识对数与指数的相互联系,会熟练地进行指数式与对数式的互化,体会转化与化归的思想;
3.了解常用对数和自然对数,了解对数的发明历史,培养学生的探究意识和发现问题、分析问题、解决问题的能力.
教学重点、难点:
重点:对数的概念,指数式与对数式的互化;
难点:对数概念的理解.
教学方法:
运用引导发现和讲练结合的教学方法,突出教师的“导”和学生的“探”.
教学过程:
一.情境设置
早在17世纪,航海、天文、贸易迅速发展,人们需要面对越来越繁难的计算,耗费的时间也越来越长.比如天文学里:
299792.458(光在真空中的速度) ×31536000(一年的秒数)=1光年(?)
为此,数学家们不断探索研究优化运算的方法,这其中不得不提苏格兰数学家纳皮尔,他在研究这样的问题时感慨到:“没有什么比大数的乘、除、开平方或开立方运算更让数学工作者头痛、更阻碍计算者的了.这不仅浪费时间,而且容易出错.因此,我开始考虑怎样消除这些障碍.经过长久的思索,我终于找到了漂亮的简短法则……”
二.数学活动
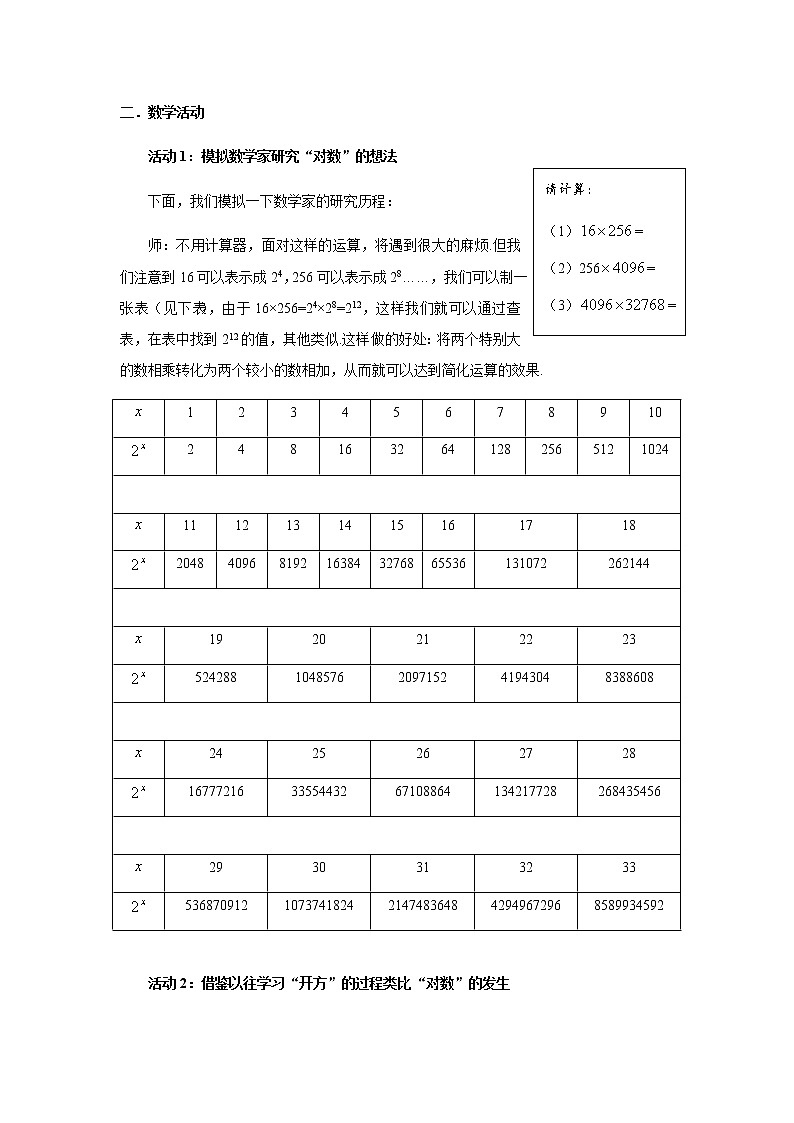
请计算:
=
256=
=
活动1:模拟数学家研究“对数”的想法
下面,我们模拟一下数学家的研究历程:
师:不用计算器,面对这样的运算,将遇到很大的麻烦.但我们注意到16可以表示成24,256可以表示成28……,我们可以制一张表(见下表),由于16×256=24×28=212,这样我们就可以通过查表,在表中找到212的值,其他类似.这样做的好处:将两个特别大的数相乘转化为两个较小的数相加,从而就可以达到简化运算的效果.
活动2:借鉴以往学习“开方”的过程类比“对数”的发生
按照上面的过程,我们若找到两个数m、n,使2m=299792.458 ,2n=31536000,那么我们就可以大大优化运算.
问1:这是一个什么方程?
——已知底数和幂,求指数.
为了研究的方便,我们取数值小点的类似问题,比如:
其实,在以前的学习中,我们也遇到类似问题:
问2:在初中,在学习开方运算时,遇到“”这样的问题,这又是一个什么方程?
——已知指数和幂,求底数.
回忆一下,当时是如何解决这个问题的呢?
为了解决这个问题,我们引入了开方运算,由于未知数x的取值由指数3和幂值2共同确定,我们引入了一个新的符号“”,将“”与2和3结合在一起来表示一个数,这个数的意义就是能使方程成立.
问3:能不能类比“开方运算”的研究过程,来解决刚才的问题?
类似地,中的未知数x是由底数2和幂值3共同确定,我们也可以引入一个新的符号,将它与2和3结合在一起来表示一个数,这个数的意义能使成立.
实际上,数学家纳皮尔就是用“”这三个字母作为表示新数的符号,将它与2,3结合在一起.因此,在问题“”中,就可以用表示使该方程成立的x的取值.读作:以2为底,3的对数.像这样的数,我们称之为“对数”(板书).
活动3:由特殊到一般,逐步归纳、抽象出“对数”概念
问题4:你还能写一些对数吗?
3b=10b=lg310;
43=N3=lg4N;
a3=7b=lga7;
……
如果将上述指数式中的底数,指数,幂全部换成字母,即a EQ \s\up4(b) =Nb=lgaN.(指明:根据前面指数的学习,我们知道:这里的a>0,a≠1. )
三.数学建构
定义
一般地,如果的次幂等于,即,那么就称是以为底的对数(lgarithm),记作,其中叫做对数的底数(base f lgarithm),叫做真数(prper number).
师:b叫做以a为底N的对数,叫做对数的底数,N叫做真数.
(教师边讲边在黑板上标示.)
问:在指数式中,a,b,N的名称叫什么?
学生回答指数式中的字母名称,教师完成上述连线图.
四.概念理解
活动4:多维度理解“对数”
【第一阶段】体会“对数可以转化为指数,对数式和指数式是等价的”.
师:大家都在积极地认识对数这个新朋友.我们一起来看看,有同学写了这样一个对数lg327.你知道它是个什么样的数吗?
师:为什么等于3呢?
——因为33 =27.
lg327=333 =27
——把对数式转化为相应的指数式,就容易理解了.
同学们能不能写一些对数式将它转化为指数式?
【小结】其实想要认识同学写的对数,只要将它转化为相应的指数式就明白了.通过刚才的认识过程,我们可以得到指数式和对数式是可以相互转化的.
【第二阶段】进一步认识对数——各个字母取值
师:大家看这几个对数是大于0的,有没有小于0的对数啊?
——有,lg2 EQ \F(1,2)=-1, lg4 EQ \F(1,4)=-1. lg4 EQ \F(1,64)=-3…….
师:有没有等于0的对数呢?
——lg31=0,,……
师:有很多,怎么表示?
——lga1=0(a>0,a≠1).
师:为什么?
——因为a0=1(a>0,a≠1).
师:对数可正可负可为0,那对数是否能取到所有的实数呢?
——从指数式a EQ \s\up4(b) =N(其中a>0且a≠1)中我们可以知道.
师:对数b可以取到一切实数,底数a>0,a≠1,真数N应满足什么要求?
——大于0.
整理得:
在对数式中,
底数a>0且a≠1;
对数属于一切实数;
真数N大于0.
【小结】通过讨论,我们认识了一些特殊的对数,知道对数b可以取到一切实数,但是真数N必须大于0.在认识对数的过程中,我们运用了对数式与指数式之间的等价转化.
【第三阶段】知识应用——求值
例题:求下列各式的值:
;
(2);
(3);
下面请看练习.
师:第一题值为多少?你是怎么想的?
(4).
(如果有同学知道答案,请他解释,重点问他怎么想到的.如果学生不知道怎么做,启发:根据我们前面认识对数的方法,遇到一个新的对数问题我们应该怎么做?转化为指数式.)
板书:(1)解:由,得.
学生板演:(2);
(3);
对于第(4)题可能学生存在困惑,可引导将对数式转化为指数式进行思考.
板书 解:设,根据对数的定义知
即,得,
,
所以
【第四阶段】认识两个“宠儿”——常用对数、自然对数
师:大家看第2小题底数是10,我们通常将以10为底的对数叫常用对数,简记为lg10 N=lg N.比如简记为,简记为.
在科学技术中,常常使用以e为底的对数,这种对数称为自然对数(natural lgarithm).e是一个无理数.正数的自然对数一般简记为,如分别记为等.
师:同学们,“常用对数”“自然对数”这两个特殊对数的名称很特别.为什么称之为常用对数?自然对数又自然在哪里?对这个内容感兴趣的同学,老师向大家推荐两本课外阅读书《不可思议的e》和《漫话e》,从中你一定能找到答案.
对数
(同一关系,两种形式)
底数
真数
常用对数
自然对数
数学家探索“对数”的过程模拟
运算
性质
函数
模型
以往学习“开方”的
经验借鉴
五.课堂小结
六.作业布置
布置作业:课本79页:习题3.2(1)感受理解 1,2,3,4
1
2
3
4
5
6
7
8
9
10
2
4
8
16
32
64
128
256
512
1024
11
12
13
14
15
16
17
18
2048
4096
8192
16384
32768
65536
131072
262144
19
20
21
22
23
524288
1048576
2097152
4194304
8388608
24
25
26
27
28
16777216
33554432
67108864
134217728
268435456
29
30
31
32
33
536870912
1073741824
2147483648
4294967296
8589934592
苏教版必修1第3章 指数函数、对数函数和幂函数3.2 对数函数3.2.1 对数教案设计: 这是一份苏教版必修1第3章 指数函数、对数函数和幂函数3.2 对数函数3.2.1 对数教案设计,共9页。教案主要包含了教学目标,教学重点,教学方法和教学手段,教学过程等内容,欢迎下载使用。
苏教版必修1第3章 指数函数、对数函数和幂函数3.2 对数函数3.2.1 对数教案: 这是一份苏教版必修1第3章 指数函数、对数函数和幂函数3.2 对数函数3.2.1 对数教案,共13页。教案主要包含了教学目标,教学重点,教学方法与手段,教学过程等内容,欢迎下载使用。
苏教版必修1第3章 指数函数、对数函数和幂函数3.2 对数函数3.2.1 对数教学设计及反思: 这是一份苏教版必修1第3章 指数函数、对数函数和幂函数3.2 对数函数3.2.1 对数教学设计及反思,共6页。













