




高中苏教版3.4.1 函数与方程课文ppt课件
展开在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障.这是一条10 km长的线路,如何迅速查出故障所在?
如果沿着线路一小段一小段查找,困难很多.每查一个点要爬一次电线杆,10km长,大约有200多根电线杆呢.想一想,维修线路的工人师傅怎样工作最合理?
这样的思想方法在生活中解答以上这类问题时经常碰到.解答以上这类实际问题关键在于,根据实际情况加以判断和总结,巧妙取中点,巧妙分析和缩小故障的区间,从而以最短的时间和最小的代价达到目的.
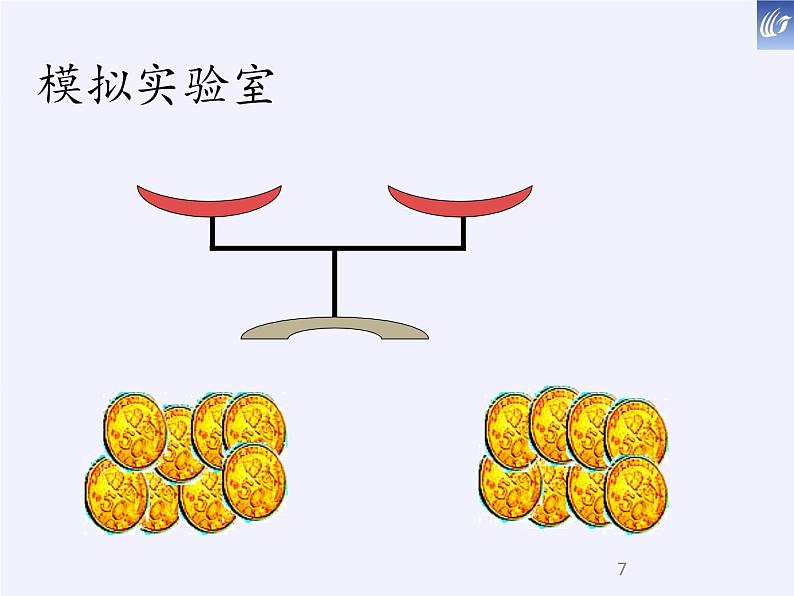
16枚金币中有一枚略轻,是假币
通过这个小实验,你能想到什么样的方法缩小零点所在的范围呢?
求方程 在区间(2,3) 的近似 解?(精确到0.1)
探究求零点近似值的方法
先画出函数 的简图,
第一步:得到初始区间(2,3)
第二步:取2与3的平均数2.5
第三步:取2与2.5的平均数2.25
最后一步:因为2.375与2.4375精确到0.1的近似值都为2.4,所以此方程的近似解为 x1≈2.4.
2.4375 -2.375=0.0625 <0.1
以上这种求零点近似值的方法叫做二分法
2.用二分法求一元方程f(x)=0的近似解的基本步骤:
第一步 确定初始区间[a,b],验证f(a)f(b)<0
第二步 求区间[a,b]两端点的平均值
第三步 计算f(c) 并判断:
(1)如果f(c)=0,则c就是f(x)的零点,计算终止;
(2)如果f(a)f(c)<0,则零点 ,否则零点 。
第四步 重复步骤2~3,直至所得区间的两端点差的绝对值小于要求的精确值,则零点的近似值为所得区间内的任一数。
一般取其中点为近似值。
求方程 的近似 解?(精确到0.1)
变式. 求方程 的近似解(精确到0.1)
例2. 求方程 的近似解(精确到0.1)
二分法是求函数零点近似解的一种计算方法.用二分法求函数零点的一般步骤:(1)零点存在性定理,求出初始区间;(2)进行计算,确定下一区间(3)循环进行,达到精确要求
⒊二分法渗透了极限和算法的思想.
数学必修13.4.1 函数与方程授课课件ppt: 这是一份数学必修13.4.1 函数与方程授课课件ppt,共8页。PPT课件主要包含了课堂小结等内容,欢迎下载使用。
苏教版必修13.4.1 函数与方程背景图课件ppt: 这是一份苏教版必修13.4.1 函数与方程背景图课件ppt,共15页。PPT课件主要包含了答案acb等内容,欢迎下载使用。
高中数学苏教版必修13.4.1 函数与方程图片ppt课件: 这是一份高中数学苏教版必修13.4.1 函数与方程图片ppt课件,共9页。PPT课件主要包含了小题训练,典型例题等内容,欢迎下载使用。













