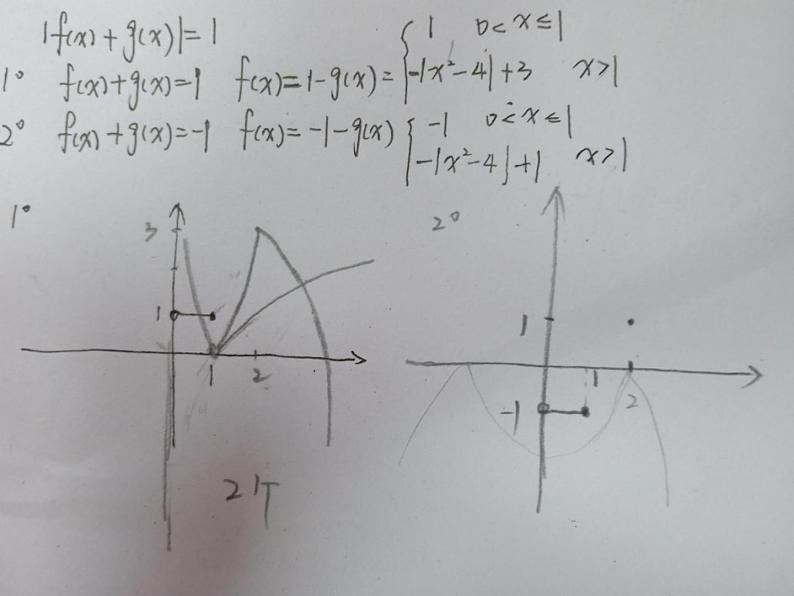
苏教版必修1第3章 指数函数、对数函数和幂函数3.4 函数的应用3.4.1 函数与方程集体备课ppt课件

这是一份苏教版必修1第3章 指数函数、对数函数和幂函数3.4 函数的应用3.4.1 函数与方程集体备课ppt课件，共19页。PPT课件主要包含了－∞－4等内容，欢迎下载使用。

热点追踪 运用数形结合思想探究函数零点问题历来是高考的热点与难点，解决此类问题的难点是函数形式的有效选择。本专题主要研究运用数形结合思想探究函数零点问题，并在解决问题的过程中感悟数学思想方法的灵活运用。
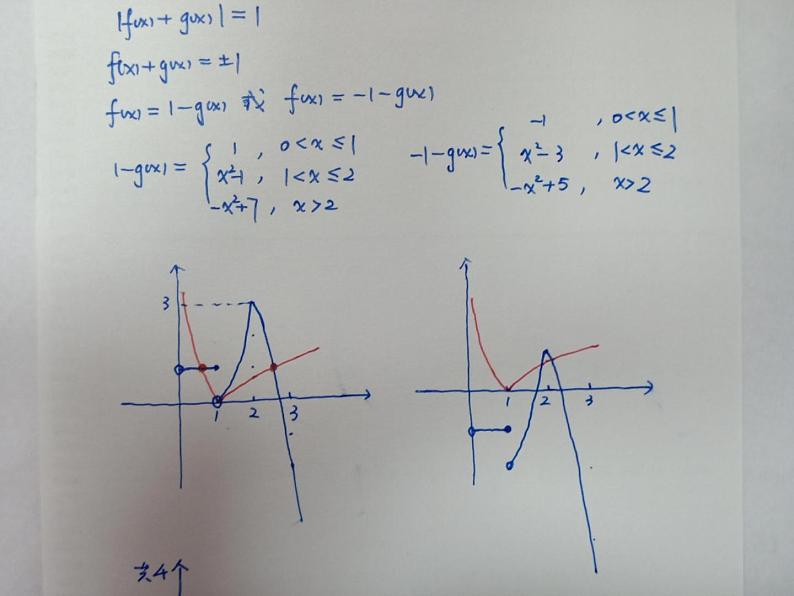
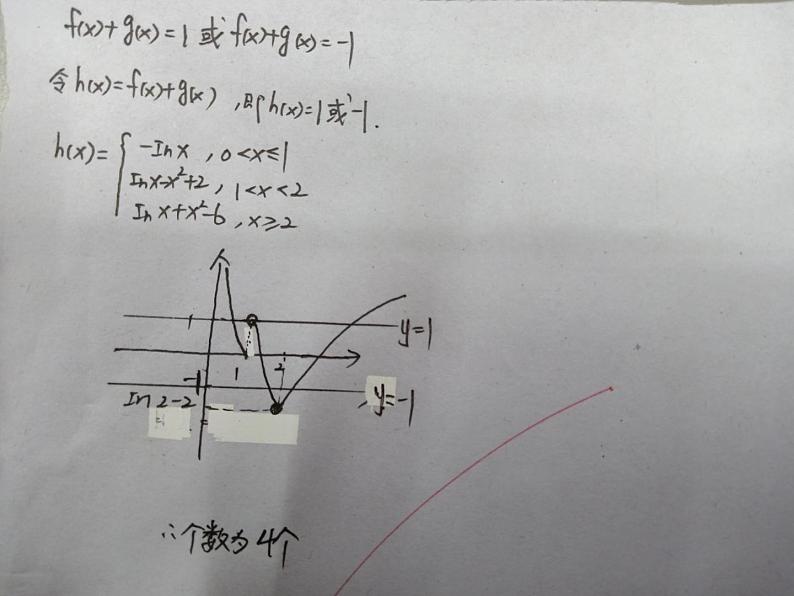
(2015·江苏)已知函数f(x)＝|ln x|，g(x)＝ 则方程|f(x)＋g(x)|＝1实根的个数为___.
解析　令h(x)＝f(x)＋g(x)，
故当1由图象可知|f(x)＋g(x)|＝1的实根个数为4.
解析　画出函数f(x)的图象如图所示，观察图象可知，若方程f(x)－a＝0有三个不同的实数根，则函数y＝f(x)的图象与直线y＝a有3个不同的交点，此时需满足0由题意知，h(x)与g(x)图象(如图所示)有三个不同的交点，
　(1)(2017届南京市、盐城市模拟)若函数f(x)＝x2－mcs x＋m2＋3m－8有惟一零点，则满足条件的实数m组成的集合为___.
解析 f(x)为偶函数且有惟一零点，所以惟一零点只能为零，由f(0)＝0，得m＝2或m＝－4.当m＝2时，y＝x2＋2与y＝2cs x有1个公共点，满足题意；当m＝－4时，y＝－x2＋4与y＝4cs x有3个公共点，不满足题意.因此，答案为
(2)已知函数f(x)＝ g(x)＝kx＋1，若方程f(x)－g(x)＝0有两个不同的实根，则实数k的取值范围是___________________.
则考虑临界情况，可知当函数g(x)＝kx＋1的图象过点A(1，e)，B(2，e)时直线斜率k1＝e－1，k2＝
解析　画出函数f(x)的大致图象如右：
并且当k＝1时，直线y＝x＋1与曲线y＝ex相切于点(0,1)，则得到当函数f(x)与g(x)图象有两个交点时，实数k的取值范围是
函数f(x)＝ 其中t>0，若函数g(x)＝f [ f(x)－1]有6个不同的零点，则实数t的取值范围是______.
令f(x)－1＝m，则m＝0或m＝t，当且仅当g(x)＝0时成立，所以条件等价于方程f(x)＝1和方程f(x)＝t＋1共6个不同的实数根，由图知等价于1<1＋t位于M，N之间，
解析　f(x)的图象如图，