高中数学苏教版必修1第3章 指数函数、对数函数和幂函数3.4 函数的应用3.4.1 函数与方程授课ppt课件

这是一份高中数学苏教版必修1第3章 指数函数、对数函数和幂函数3.4 函数的应用3.4.1 函数与方程授课ppt课件，共20页。PPT课件主要包含了二次函数的解析式，二次函数的图象，二次函数的性质，fk0，典型例题，∴n8，∵f2-1，∴a-4，∴b-c，解得c≥24等内容，欢迎下载使用。
1.一般式: y=ax2+bx+c(a≠0);
2.顶点式: y=a(x -m)2+n(其中(m, n)为抛物线的顶点坐标);
3.两根式: y=a(x -x1)(x -x2)(其中x1, x2为抛物线与 x 轴两交点 的横坐标);
　 注: 求二次函数的解析式, 一般都采用待定系数法. 做题时,要根据题设条件, 合理地设出解析式.
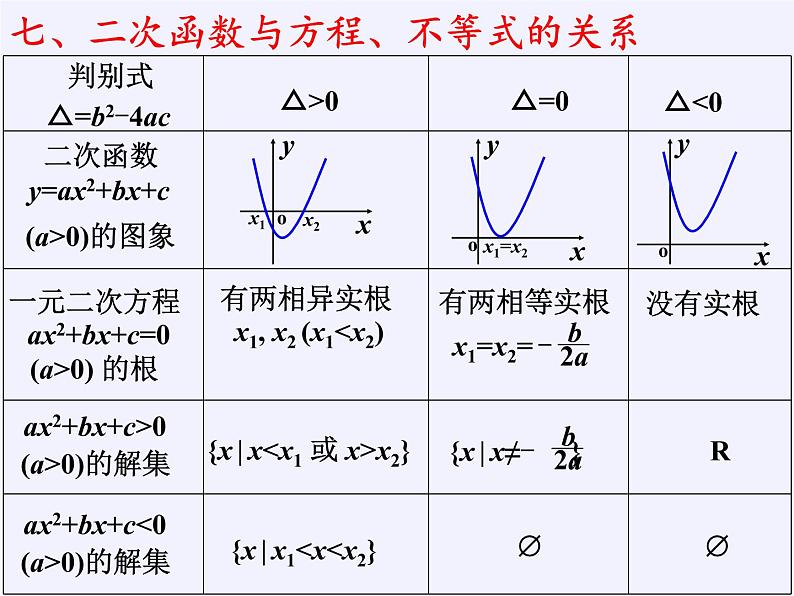
　　有关知识: 图象形状; 对称轴; 顶点坐标; 与 x 轴交点坐标;截 x 轴线段长.
四、二次函数f(x)=ax2+bx+c(a>0)在[m, n]上的最值
2.若 x0[m, n], 则
(1)当 x0n 时, f(x)min=f(n), f(x)max=f(m).
五、不等式 ax2+bx+c>0 恒成立问题
1. ax2+bx+c>0在R上恒成立. 
ax2+bx+c0(a>0) 在 [m, n] 上恒成立. 
 f(x)min>0(x∈[m, n])
f(x)=ax2+bx+c0) 在 [m, n] 上恒成立. 
1.方程 f(x)=0 有两正根 
六、二次方程 ax2+bx+c=0(a>0) 的实根分布问题
记 f(x)=ax2+bx+c(a>0),
2.方程 f(x)=0 有两负根 
4.方程 f(x)=0 的两实根都小于 k 
3.方程 f(x)=0 有一正根一负根 
5.方程 f(x)=0 的两实根一个大于 k, 另一个小于 k 
6.方程 f(x)=0 的两实根都大于 k
7.方程 f(x)=0 的两实根都在区间(m, n)内
8.方程 f(x)=0 的两实根中, 有且只有一个在区间(m, n)内.
 f(m)f(n)1, ∴a=5.
(2)当 3-2a≥a, 即 00, 求实数 a 的取值范围.
解: f(x) 的图象是开口向上的抛物线, 其对称轴为直线 x=a-1.
(1)问题等价于“对于 x∈[-1, 1], 有 f(x)max>0.”
①当 a-1≤0 即 a≤1 时, f(x)max=f(1)=-a2-2a+15.
由 -a2-2a+15>0 得: -50 得: -1