苏教版必修11.2 子集、全集、补集课堂教学课件ppt

这是一份苏教版必修11.2 子集、全集、补集课堂教学课件ppt，共16页。

1.复习元素与集合的关系——　　　属于与不属于的关系，并填空：
⑶－1.5____R
2.类比实数的大小关系，如5<7，2≤2，试想集合间是否有类似的“大小”关系呢？
问题1.观察下列各组集合，A与B具有怎样的关系？如何用数学语言来表达这种关系？⑴A＝{－1,1}, B＝{－1,0,1,2}⑵A＝N，B＝R⑶A＝{x｜x为高一⑶班的男生}，　B＝{y|y为高一⑶班的团员}⑷A＝{x｜x为高一年级的男生}，　B＝{y|y为高一年级的女生}
1.集合与集合之间的“包含”关系
　如果集合A的任何一个元素都是集合B的元素，则称集合A是集合B的子集（subset），记为A⊆B或B⊇A，读作：A包含于（is cntained in）集合B”，或“集合B包含（cntains）集合A”.
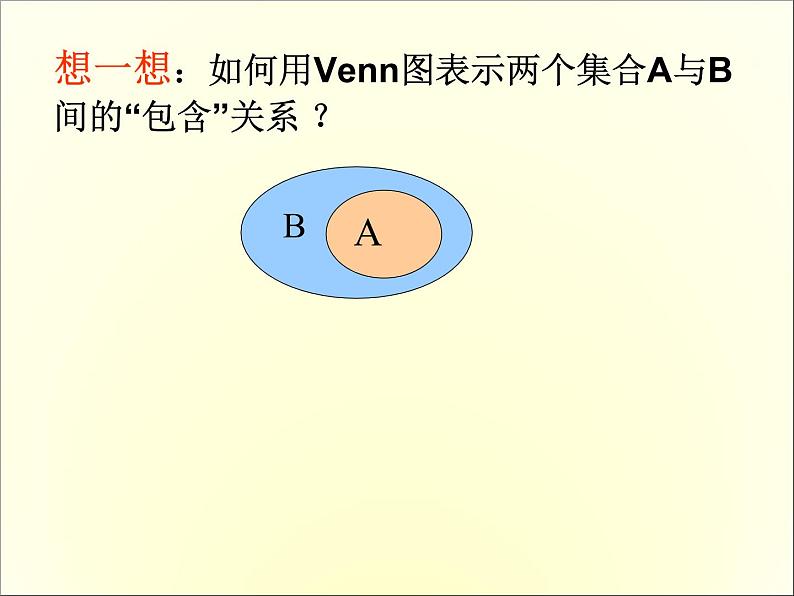
想一想：如何用Venn图表示两个集合A与B间的“包含”关系 ？
思考：以下式子成立吗？⑴A⊆A；⑵Φ⊆A；⑶Φ⊆Φ.
想一想： A⊆B与B⊇A能否同时成立？你能举出一个例子吗？
2.集合与集合之间的 “相等”关系：若A⊆B或B⊇A，则A＝B.
3.真子集的概念若集合A⊆B，存在元素x∈B且x∉A，则称集合A是集合B的真子集（prper subset）。记作：A
A）读作：A真包含于
例1写出集合{a，b}的所有的子集.
解析：Ø,{a},{b},{a,b}
变：写出集合{a，b，c}的所有的子集.
解析：Ø,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}
猜想：若A中有n个元素，A的子集有___个.
例2下列三个集合中,哪两个集合具有包含关系？⑴S＝{―2,―1,1,2},A＝{―1,1},B＝{―2,2}；⑵S＝R,A＝{x|x≤0,x∈R},B＝{x|x＞0,x∈R}；⑶S＝{x|x为地球人}，A＝{x|x为中国人}，B＝{x|x为外国人}.
思考：观察例2中每一组的三个集合，它们之间还有一种什么关系？
4.补集的概念 补集的定义：设A⊆S，由S中不属于A的所有元素组成的集合称为S的子集A的补集cmplementary set）,简称为集合A的补集，记作：CUA（读作A在S中的补集）即：CUA＝{x|x∈U且x∉A}.
想一想：如何用Venn图表示CU A？
想一想：CUA在S中的补集等于什么？
说明：补集的概念必须要有全集的限制
　　如果集合S包含我们所要研究的各个集合，这时S可以看做一个全集，全集通常记为U.
的解集为A，U＝R，试求A及CUA.
点评：不等式问题通常借助数轴来研究，　　　但要注意实心点与空心点.