2021学年第2章函数综合与测试复习ppt课件

展开

这是一份2021学年第2章函数综合与测试复习ppt课件，共30页。PPT课件主要包含了栏目索引，知识点一映射与函数，解析答案，即x≤1且x≠0，画出图象如图所示，题型三抽象函数问题，∵x2x10，分类讨论思想，解决思想方法，函数图象如图1等内容，欢迎下载使用。

一、知识网络整体构建
二、要点归纳主干梳理
三、题型探究重点突破
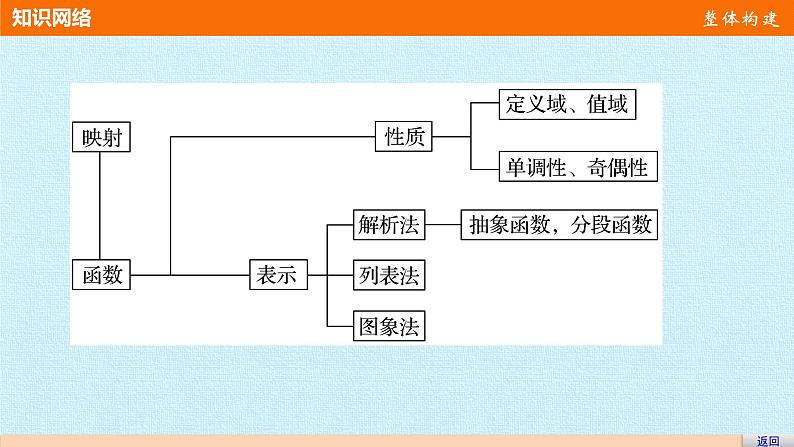
知识网络整体构建
已知A，B是两个非空集合，在对应法则f的作用下，对于A中的任意一个元素x，在B中都有唯一的一个元素与之对应，这个对应叫做从A到B的映射，记作f：A→B.由定义可知在A中的任意一个元素在B中都能找到唯一的像，而B中的元素在A中未必有原像.若f：A→B是从A到B的映射，且B中任一元素在A中有且只有一个原像，则这样的映射叫做从A到B的一一映射.函数是一个特殊的映射，其特殊点在于A，B都为非空数集，函数有三要素：定义域、值域、对应法则.两个函数只有当定义域和对应法则分别相同时，这两个函数才是同一函数.
要点归纳主干梳理
1.函数的单调性主要涉及求函数的单调区间，利用函数的单调性比较函数值的大小，利用函数的单调性解不等式等相关问题.深刻理解函数单调性的定义是解答此类问题的关键.2.函数单调性的证明根据增函数、减函数的定义分为四个步骤证明，步骤如下：(1)取值：任取x1，x2∈D，且x10；(2)作差变形：Δy＝y2－y1＝f(x2)－f(x1)＝…，向有利于判断差的符号的方向变形；
知识点二　函数的单调性
(3)判断符号：确定Δy的符号，当符号不确定时，可以进行分类讨论；(4)下结论：根据定义得出结论. 3.证明函数单调性的等价变形：(1)f(x)是单调递增函数⇔任意x1(2)f(x)是单调递减函数⇔任意x1对于定义域内的任意x(定义域关于原点对称)
知识点三　函数的奇偶性
性质：①函数y＝f(x)是偶函数⇔f(x)的图象关于y轴对称.②函数y＝f(x)是奇函数⇔f(x)的图象关于原点对称.③偶函数在其定义域内关于原点对称的两个区间上的单调性相反.④奇函数在其定义域内关于原点对称的两个区间上的单调性相同，奇函数f(x)在x＝0处有定义时，必有y＝f(x)的图象过原点，即f(0)＝0.
题型一　函数的概念与性质
研究函数往往从定义域、值域、单调性、奇偶性、对称性入手，分析函数的图象及其变化趋势，对函数性质的考查体现了“小”、“巧”、“活”的特征，做题时应注重上述性质知识间的融合.
题型探究重点突破
比较得n＝－n，n＝0.
解　∵f(x)是奇函数，∴f(－x)＝－f(x)，
(1)求实数m和n的值；
因此，实数m和n的值分别是2和0.
(2)求函数f(x)在区间[－2，－1]上的最值.
任取x1，x2∈[－2，－1]，且x1＜x2，
∵－2≤x1＜x2≤－1时，∴x1－x2＜0，x1x2＞0，x1x2－1＞0，
∴f(x1)－f(x2)＜0，即f(x1)＜f(x2).
∴函数f(x)在[－2，－1]上为增函数，
(2)定义在R上的函数f(x)满足f(x＋1)＝2f(x).若当0≤x≤1时，f(x)＝x(1－x)，则当－1≤x≤0时，f(x)＝________.
解析　设－1≤x≤0，则0≤x＋1≤1，所以f(x＋1)＝(x＋1)[1－(x＋1)]＝－x(x＋1).又因为f(x＋1)＝2f(x)，
(－∞，0)∪(0,1]
题型二　函数图象及其应用
函数的图象是函数的重要表示方法，它具有明显的直观性，通过函数的图象能够掌握函数重要的性质，如单调性、奇偶性等.反之，掌握好函数的性质，有助于图象正确的画出.函数图象广泛应用于解题过程中，利用数形结合解题具有直观、明了、易懂的优点.
例2　对于函数f(x)＝x2－2|x|.(1)判断其奇偶性，并指出图象的对称性；
解　函数的定义域为R，关于原点对称，f(－x)＝(－x)2－2|－x|＝x2－2|x|.则f(－x)＝f(x)，∴f(x)是偶函数.图象关于y轴对称.
根据图象知，函数f(x)的最小值是－1.单调增区间是[－1,0]，[1，＋∞)；单调减区间是(－∞，－1]，[0,1].
(2)画此函数的图象，并指出单调区间和最小值.
如图，分别画出三个函数的图象，得到三个交点A(0,3)，B(1,2)，C(5,8).
f(x)的图象是图中的实线部分，图象的最低点是点B(1,2)，所以f(x)的最小值是2.
从图象观察可得函数f(x)的表达式：
抽象函数是指没有明确给出具体的函数表达式，只是给出一些特殊关系式的函数，它是高中数学中的一个难点，高考中经常出现关于抽象函数的试题.因为抽象，解题时思维常常受阻，思路难以展开.抽象函数问题一般是由所给的性质，讨论函数的单调性、奇偶性、图象的对称性，或是求函数值、解析式等.主要处理方法是“赋值法”，通常是抓住函数特性，特别是定义域上恒等式，利用变量代换解题.
例3　函数f(x)对一切实数x，y，都有f(x＋y)＝f(x)＋f(y)，且当x>0时，f(x)>0，试判断函数f(x)的单调性，并说明理由.
解　方法一　设任意的x1，x2∈R，且x10.由条件x>0时，f(x)>0，∴f(x2－x1)>0.又f(x1)－f(x2)＝f(x1)－f((x2－x1)＋x1)＝f(x1)－f(x2－x1)－f(x1)＝－f(x2－x1)<0，∴f(x1)－f(x2)<0，
方法二　设x1∈R，令x2＝x1＋a(a>0)，则x10时，f(a)>0，∴f(x1)－f(x2)<0，
即f(x1)∴函数f(x)为R上的增函数.
跟踪训练3　已知函数f(x)的定义域是x≠0的一切实数，对定义域内的任意x1，x2，都有f(x1x2)＝f(x1)＋f(x2)，且当x>1时，f(x)>0.求证：(1)f(x)是偶函数；
证明　令x1＝x2＝1，得f(1)＝2f(1)，∴f(1)＝0.令x1＝x2＝－1，得f(1)＝f[(－1)×(－1)]＝f(－1)＋f(－1)，∴f(－1)＝0.∴f(－x)＝ f [(－1)×x]＝f(－1)＋f(x)＝f(x).∴f(x)是偶函数.
(2)f(x)在(0，＋∞)上是单调递增的.
证明　设0即f(x2)－f(x1)>0.∴f(x2)>f(x1).∴f(x)在(0，＋∞)上是单调递增的.
分类讨论思想的实质：把整体问题化为部分来解决，化成部分后，从而增加题设条件，在解决含有字母参数的问题时，常用到分类讨论思想，分类讨论要弄清对哪个字母进行分类讨论，分类的标准是什么，分类时要做到不重不漏.本章中涉及到分类讨论的知识点为：集合运算中对∅的讨论，二次函数在闭区间上的最值问题，函数性质中求参数的取值范围问题等.
例4　设函数f(x)＝x2－2x＋2，x∈[t，t＋1]，t∈R，求函数f(x)的最小值.
解　f(x)＝x2－2x＋2＝(x－1)2＋1，x∈[t，t＋1]，t∈R，对称轴为x＝1.
当t＋1<1，即t<0时，
当t≤1≤t＋1，即0≤t≤1时，函数图象如图(2)，
函数f(x)在区间[t，t＋1]上为减函数，所以最小值为f(t＋1)＝t2＋1；
最小值为f(1)＝1；
当t>1时，函数图象如图(3)，函数f(x)在区间[t，t＋1]上为增函数，所以最小值为f(t)＝t2－2t＋2.
跟踪训练4　求函数y＝－x(x－a)在x∈[－1，a]上的最大值.
又∵x∈[－1，a]，
由图②可知ymax＝f(a)＝0.
综上所述，当－1