高中数学苏教版必修13.4.2 函数模型及其应用多媒体教学ppt课件

这是一份高中数学苏教版必修13.4.2 函数模型及其应用多媒体教学ppt课件，共22页。PPT课件主要包含了高考再现，三角形常用公式，1正弦定理，复习回顾，余弦定理，课前预习，变式训练，例题分析，当堂巩固，课堂总结等内容，欢迎下载使用。
1（2013江苏高考题18）如图，游客从某旅游景区的景点处下山至 C处有两种路径. 一种是A从沿 直线步行到 C，另一种是先从 A沿索道乘缆车到B ，然后从B 沿直线步行到C .现有甲、乙两位游客从 处下山，甲沿 AC匀速步行，速度为50m/min. 在甲出发2min后，乙从 A乘缆车到 B，在 B处停留1min后，再从B 匀速步行到C . 假设缆车匀速直线运动的速度为130m/min，山路 长为1260m，经测量，
(1) 求索道 的长；(2) 问乙出发多少分钟后，乙在缆车上与甲的距离最短？(3) 为使两位游客在 处相互等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？
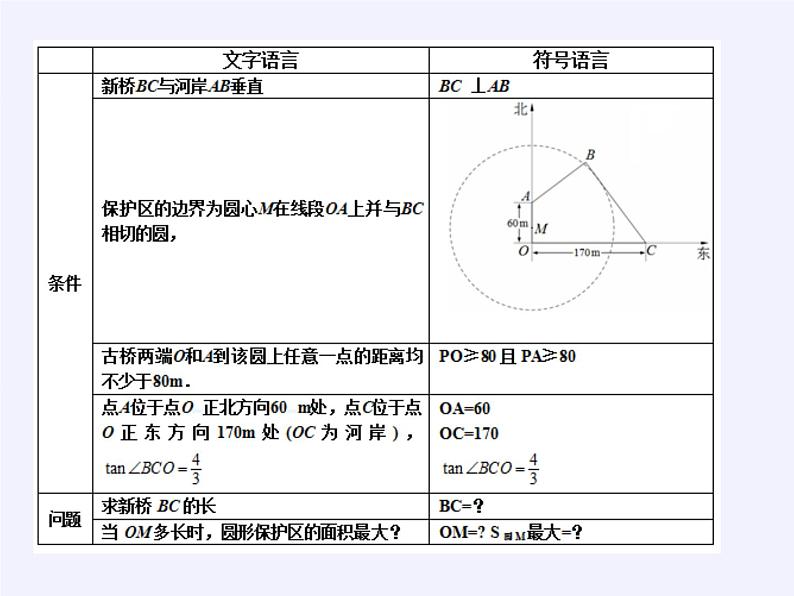
2（2014江苏高考题18）如图，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区．规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80m．经测量，点A位于点O学科王正北方向60m处，点C位于点O正东方向170m处(OC为河岸)， ．
（1）求新桥BC的长；（2）当OM多长时，圆形保护区的面积最大？
3.（2015年江苏高考17题）17.某山区外围有两条相互垂 直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路的山区边界的直线型公 路，记两条相互垂直的公路为 ，山区边界曲线为C，计划修建 的公路为l，如图所示，M，N为C的两个端点，测得点M到 的距离分别为5千米和40千米，点N到 的距离分别为20千米和2.5千米，以 所在的直线分别为x，y轴，建立平面直角坐 标系xOy，假设曲线C符合函数 (其中a，b为常数）模型.
（1）求a，b的值；（2）设公路l与曲线C相切于P点，P的横坐标为t. ①请写出公路l长度的函数解析式 ，并写出其定义域； ②当t为何值时，公路l的长度最短？求出最短长度.
问题：三条高考题分别考查了什么？
15年高考考点三：考查函数的概念，导数的几何意义及其应用，考查建立数学模型及运用数学知识解决实际问题的能力
13年高考考点一：考查三角形正余弦定理的应用、二次函数的最值及三角函数的关系式、两角和的正弦等基础知识，考查数学阅读能力和分析解决实际问题的能力
14年高考考点二：考查直线方程、直线与圆的位置关系和解三角形等基础知识，考查建立数学模型及运用数学知识解决实际问题的能力
（2）正弦定理应用范围：
①已知两角和任意边，求其他两边和一角
②已知两边和其中一边的对角，求另一边的对角。(注意解的情况)
（4）、余弦定理可以解决以下两类有关三角形问题：（1）已知三边求三个角；（2）已知两边和它们的夹角，求第三边和其他两个角。
1、正余弦定理及不等式的应用：如图，某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树，已知角A为120°，AB,AC的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆.（1）若围墙AP,AQ总长度为200米，如何围可使得三角形地块APQ的面积最大？（2）已知AP段围墙高1米，AQ段围墙高1.5米，造价均为每平方米100元.若围围墙用了20000元，问如何围可使竹篱笆用料最省？
（1）准确地理解题意；(审题)（2）正确地作出图形；把已知和要求的量尽量 集中在有关三角形中，利用正弦定理和 余弦定理建立等量关系（建模） （3）根据关系，合理选择方法求解（解模）（４）再根据实际意义和精确度的要求给出　　　答案．（评价、作答）
解三角形应用题的一般步骤：
如图，某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树，已知角A为120°，AB,AC的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆.（1）若PQ处竹篱笆长200米，如何围可使得三角形地块APQ的面积最大？
例1、正余弦定理及不等式的应用：海岸线 ， 现用长为 的拦网围成一养殖场，其中 ．（1）若 , 求养殖场面积最大值；
（3）若(2)中B、C可选择，求四边形养殖场ACDB面积的最大值.
如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上.（1）设AD＝x，ED＝y，求用x表示y的函数关系式；（2）如果DE是灌溉水管，为节约成本，希望它最短，DE的位置应在哪里？如果DE是参观线路，则希望它最长，DE的位置又应在哪里？请予证明
1、应用题蕴含数学思想：
第一、函数思想。函数思想方法是高中数学的重要思想方法，贯穿于高中数学理论与应用的各个领域，它是用联系变化观点提取数学对象，抽象其数学特征，建立函数关系，将问题转化。
第二、转化思想。转化思想是把待解决或难解决的问题，通过某种通欲演变，使问题解决或较易解决 ，最终求得原问题解决的思维方法，解函数应用题常常是先将文字语言“翻译”成数学语言，再转化为数学问题。
第三、建模思想。建模思想是通过对问题的数学量化，模型构建和求解检验，使问题获解的思想方法。用建模思想解应用题一般解题流程：审题→建模→解模→评价→作答
2、分析和解决函数应用题时，不仅仅掌握这几种基本思想方法，还需要熟练应用学科知识解决模型中的最值问题、可行不可行问题、范围问题等等。
3、作答应用题答案注意叙述条理清晰，答案完整