高中数学人教B版 (2019)必修 第四册9.2 正弦定理与余弦定理的应用同步训练题

这是一份高中数学人教B版 (2019)必修 第四册9.2 正弦定理与余弦定理的应用同步训练题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 如图，设A，B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45∘，∠CAB=105∘后，就可以计算出A，B两点的距离为( )

A.502mB.503mC.252mD.2522m

2. 如图所示，为了测量某湖泊两侧A，B间的距离，某同学首先选定了与A，B不共线的一点C，然后给出了四种测量方案：(△ABC的角A，B，C所对的边分别为a，b，c)
①测量A，C，b．②测量a，b，C．③测量A，B，a．④测量a，b，B．
则一定能确定A，B间距离的所有方案的序号为( )

A.①②③B.②③④C.①③④D.①②③④

3. 小赵开车从A处出发，以每小时40千米的速度沿南偏东40∘的方向直线行驶，30分钟后到达B处，此时，小王发来微信定位，显示他自己在A的南偏东70∘方向的C处，且A与C的距离为千米，若此时，小赵以每小时52千米的速度开车直线到达C处接小王，则小赵到达C处所用的时间大约为（ ）

A.10分钟B.15分钟C.20分钟D.25分钟

4. 如图，某建筑物的高度BC＝300m，一架无人机Q上的仪器观测到建筑物顶部C的仰角为15∘，地面某处A的俯角为45∘，且∠BAC＝60∘，则此无人机距离地面的高度PQ为（ ）

A.100mB.200mC.300mD.400m

5. 某人在A处向正东方向走xkm后到达B处，他向右转150∘，然后朝新方向走3km到达C处，结果他离出发点恰好3km，那么x的值为( )
A.3B.23C.33D.3

6. 如图，设△ABC的内角A，B，C所对的边分别为a，b，c，3(acsC+ccsA)＝2bsinB，且∠CAB=π3．若点D是△ABC外一点，DC＝1，DA＝3，下列说法中，正确的命题是（ ）

A.△ABC的内角B=π3
B.△ABC的内角C=π3
C.四边形ABCD面积的最大值为532+3
D.四边形ABCD面积无最大值
二、填空题

海洋蓝洞是地球罕见的自然地理现象，被誉为“地球给人类保留宇宙秘密的最后遗产”，我国拥有世界上已知最深的海洋蓝洞，若要测量如图所示的海洋蓝洞的口径(即A，B两点间的距离)，现取两点C，D，测得CD=80，∠ADB=135∘，∠BDC=∠DCA=15∘，∠ACB=120∘，则图中海洋蓝洞的口径为________.


《周髀算经》是我国最古老的天文学与数学著作，书中讨论了测量“日高”（太阳高度）的方法．大意为：“在A，B两处立表（古代测望用的杆子，即“髀”），设表高均为h，测得表距为d，两表日影长度差为ɛ(ɛ>0)，则可测算出日高”由所学知识知，日高H＝________．（用h，d，ɛ表示）


一艘船从A点沿北偏东70∘的方向行驶10海里至海岛B，又从B沿北偏东10∘的方向行驶10海里至海岛C，若次轮船从A点直接沿直线行驶至海岛C，则此船沿________方向行驶________海里至海岛C．
三、解答题

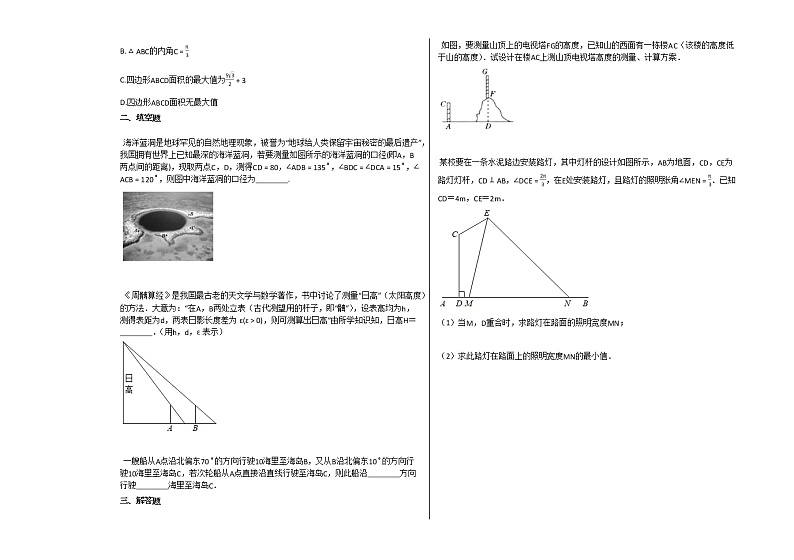
如图，要测量山顶上的电视塔FG的高度，已知山的西面有一栋楼AC（该楼的高度低于山的高度）．试设计在楼AC上测山顶电视塔高度的测量、计算方案．


某校要在一条水泥路边安装路灯，其中灯杆的设计如图所示，AB为地面，CD，CE为路灯灯杆，CD⊥AB，∠DCE=2π3，在E处安装路灯，且路灯的照明张角∠MEN=π3．已知CD＝4m，CE＝2m．

（1）当M，D重合时，求路灯在路面的照明宽度MN；

（2）求此路灯在路面上的照明宽度MN的最小值．
参考答案与试题解析
人教B版（2019）必修第四册《9.2 正弦定理与余弦定理的应用》2021年同步练习卷（2）
一、选择题
1.
【答案】
A
【考点】
解三角形
正弦定理的应用
【解析】
依题意在A，B，C三点构成的三角形中利用正弦定理，根据AC，∠ACB，B的值求得AB
【解答】
解：由题意可知，∠B=180∘−∠ACB−∠CAB=30∘，
由正弦定理得ABsin∠ACB=ACsin∠B，
∴ AB=AC×sin∠ACBsin∠B=50×2212=502，
故A，B两点的距离为502m.
故选A.
2.
【答案】
A
【考点】
解三角形的实际应用
正弦定理
【解析】
根据图形，可以知道a，b可以测得，角A、B、C也可测得，利用测量的数据，求解A，B两点间的距离唯一即可．
【解答】
解：对于①③可以利用正弦定理确定唯一的A，B两点间的距离．
对于②直接利用余弦定理即可确定A，B两点间的距离．
对于④测量a，b，B，asinA=bsinB，sinA=asinBb，此时A不唯一
故选A．
3.
【答案】
B
【考点】
解三角形
【解析】
根据题意，利用余弦定理求出BC的值，再根据路程、速度计算所需的时间．
【解答】
由题意知，△ABC中＝20，∠BAC＝70∘−40∘＝30∘，
由余弦定理得，BC2＝AB6+AC2−2⋅AB⋅AC⋅cs∠BAC
＝208+−7×20×15，
解得BC＝5≈5×2.4＝13（千米），
又13÷52＝（小时），，
所以小赵到达C处所用的时间大约为15分钟．
4.
【答案】
B
【考点】
解三角形
【解析】
在Rt△ABC中求得AC的值，△ACQ中求得AQ的值，在Rt△APQ中求得PQ的值．
【解答】
根据题意，可得Rt△ABC中，BC＝300，
∴ AC＝＝＝200；
△ACQ中，∠AQC＝45∘+15∘＝60∘，
∴ ∠QCA＝180∘−∠AQC−∠QAC＝45∘，
由正弦定理，得＝，
解得AQ＝＝200，
在Rt△APQ中，PQ＝AQsin45∘＝200×．
5.
【答案】
A,B
【考点】
正弦定理
【解析】
根据正弦定理求出角A的值，再根据三角形的性质即可求出AB的值．
【解答】
解：如图所示，
由题意知AB=x，BC=3，AC=3，B=30∘，
由正弦定理得ACsinB=BCsinA，
解得sinA=BC⋅sinBAC=3×123=32.
又A∈(0∘, 180∘)，
当A=60∘时，C=180∘−30∘−60∘=90∘，此时x=23；
当A=120∘时，C=180∘−30∘−120∘=30∘，此时x=3.
故选AB.
6.
【答案】
A,B,C
【考点】
命题的真假判断与应用
【解析】
因为3(acsC+ccsA)=2bsinB，所以3(2RsinAcsC+2RsinCcsA)＝2×2RsinB⋅sinB，所以sinB=32，B=π3．故A正确．因为∠CAB=π3．C=π3，故B正确．等边△ABC中，设AC＝x，x>0，在△ADC中，由余弦定理可得：AC2＝AD2+CD2−2AD⋅CD⋅csD，由于AD＝3，DC＝1，代入上式可得：x2＝10−6csD，所以S四边形ABCD＝S△ABC+S△ACD=12x⋅xsinπ3+12⋅3sinD=34x2+32sinD=34(10−6csD)+32sinD=3sin(D−π3)+532，所以四边形ABCD面积的最大值为532+3，故C正确．
【解答】
∵ 3(acsC+ccsA)=2bsinB，
∴ 3(sinAcsC+sinCcsA)＝2sinB⋅sinB，
∴ sinB=32，
∴ B=π3．故A正确．
又∵ ∠CAB=π3．
∴ C=π3，故B正确．
等边△ABC中，设AC＝x，x>0，
在△ADC中，由余弦定理可得：AC2＝AD2+CD2−2AD⋅CD⋅csD，
由于AD＝3，DC＝1，代入上式可得：x2＝10−6csD
∴ S四边形ABCD＝S△ABC+S△ACD=12x⋅xsinπ3+12⋅3sinD=34x2+32sinD=34(10−6csD)+32sinD=3sin(D−π3)+532，
∴ 四边形ABCD面积的最大值为532+3，故C正确．
二、填空题
【答案】
805
【考点】
解三角形
余弦定理
正弦定理
【解析】
根据题意画出图形，△BCD中利用正弦定理求出BD的值，△ACD中利用等角对等边求出AD的值，再在△ABD中由余弦定理求得AB的值．
【解答】
解：如图所示，
在△BCD中，CD=80，∠BDC=15∘，
∠BCD=∠ACB+∠DCA
=120∘+15∘=135∘，
所以∠CBD=30∘.
由正弦定理得：BDsin135∘=80sin30∘，
解得BD=80×2212=802，
在△ACD中，CD=80，∠DCA=15∘，
∠ADC=∠ADB+∠BDC
=135∘+15∘=150∘，
所以∠CAD=15∘，
所以AD=CD=80；
在△ABD中，由余弦定理得：
AB2=AD2+BD2−2AD⋅BD⋅cs∠ADB
=802+(802)2−2×80×802×cs135∘
=802×5，
所以AB=805，即A，B两点间的距离为805.
故答案为：805.
【答案】
H(e+d)e
【考点】
解三角形
三角形的面积公式
【解析】
先根据已知条件以及三角形相似列出两个等量关系，联立求解即可．
【解答】
如图；
设AE＝x，AD＝a；
由题意得：BC＝x+ɛ；AB＝d；
在△ODE 中，由三角形相似可得hH=xx+a①
在△ODC 中，由三角形相似可得hH=x+ex+e+d+a②
①②联立可得：xx+a=x+ex+e+d+a；
整理得：x=ead③；
③代入①整理得：H=h(d+e)e．
【答案】
北偏东40∘,10
【考点】
解三角形
【解析】
根据题意画出图形，结合图形利用三角形的边角关系，即可求出结果．
【解答】
如图所示，
设AB的延长线为BE，则∠CBE＝70∘−10∘＝60∘
又AB＝BC＝10，所以∠CAB＝∠ACB，
所以∠CAB＝∠ACB＝30∘，即为北偏东40∘，
等腰三角形ABC，底角为30∘，
所以底边长为AC＝2ABcs30∘＝2×10×＝10．
三、解答题
【答案】
楼高AC可测量|AC|＝a，设山的高度FD＝b，电视塔的高度GF＝h，
第一步在点A处测量点F的仰角α，在点C处测量点F的仰角β，
由题意可知tanα＝＝，tanβ＝，
∴ ，
∴ b＝，
第二步在点A处测量点G的仰角θ1，在点C处测量点G的仰角θ2，
由题意可知tanθ7＝，，
∴ ，
∴ ，
∴ h＝．
【考点】
解三角形
【解析】
利用题中的条件，分别在楼底和楼顶测量塔顶G的仰角，利用解三角形，即可解出．
【解答】
楼高AC可测量|AC|＝a，设山的高度FD＝b，电视塔的高度GF＝h，
第一步在点A处测量点F的仰角α，在点C处测量点F的仰角β，
由题意可知tanα＝＝，tanβ＝，
∴ ，
∴ b＝，
第二步在点A处测量点G的仰角θ1，在点C处测量点G的仰角θ2，
由题意可知tanθ7＝，，
∴ ，
∴ ，
∴ h＝．
【答案】
路灯在路面的照明宽度为732m；
照明宽度MN的最小值为1033m
【考点】
余弦定理
【解析】
（1）直接利用余弦定理和三角函数关系式的恒等变换的应用求出结果．
（2）利用余弦定理和正弦定理的应用及相关的运算的应用求出结果．
【解答】
当M，D重合时，
由余弦定理知，ME=DE=CD2+CE2−2CD⋅CE⋅cs∠DCE=27，
所以cs∠CDE=CD2+DE2−CE22CD⋅DE=5714，
因为∠CDE+∠EMN=π2，
所以sin∠EMN=cs∠CDE=5714，
因为cs∠EMN>0，
所以cs∠EMN=1−sin2∠EMN=2114，
因为∠MEN=π3，
所以sin∠ENM=sin(2π3−∠EMN)=sin2π3cs∠EMN−cs2π3sin∠EMN=277．
∴ 在△EMN中，由正弦定理可知，MNsin∠MEN=EMsin∠ENM，解得MN=732；
易知E到地面的距离h=4+2sin(2π3−π2)=5m，
由三角形面积公式可知，S△EMN=12⋅MN⋅5=12EM⋅EN⋅sinπ3，
所以103MN=EM⋅EN，
又由余弦定理可知，MN2=EM2+EN2−2EM⋅EN⋅csπ3≥EM⋅EN，
当且仅当EM＝EN时，等号成立，
所以MN2≥103MN，解得MN≥1033；