黑龙江省大庆中学2022届高三上学期开学考试数学（文）试题+Word版含答案

大庆中学2021--2022学年度上学期开学考

高三文科数学试题

试卷总分：150分考试时间：120分钟

注意事项：

1．答题前填写好自己的姓名、班级、考号等信息

2．请将答案正确填写在答题卡上

一、选择题：（本大题共12个小题，每小题5分，共60分）

1．集合，，则（    ）

A． B． C． D．

2．已知复数，则z的虚部为（    ）

A． B． C．－2 D．2

3．已知命题；命题，则下列说法正确的是（    ）

A．是假命题 B．是真命题 C．是真命题 D．是假命题

4．若函数 ，则=（　　）

A． B． C． D．0

5．函数的定义域为（    ）

A． B． C． D．

6．函数y=ax在[0，1]上最大值与最小值的和为3，则a=

A．2 B． C．4 D．

7．设，则是

A．奇函数，且在上是增函数 B．奇函数，且在上是减函数

C．有零点，且在上是减函数 D．没有零点，且是奇函数

8．下列结论：①;②③④.

其中正确的有

A．个 B．个 C．个 D．个

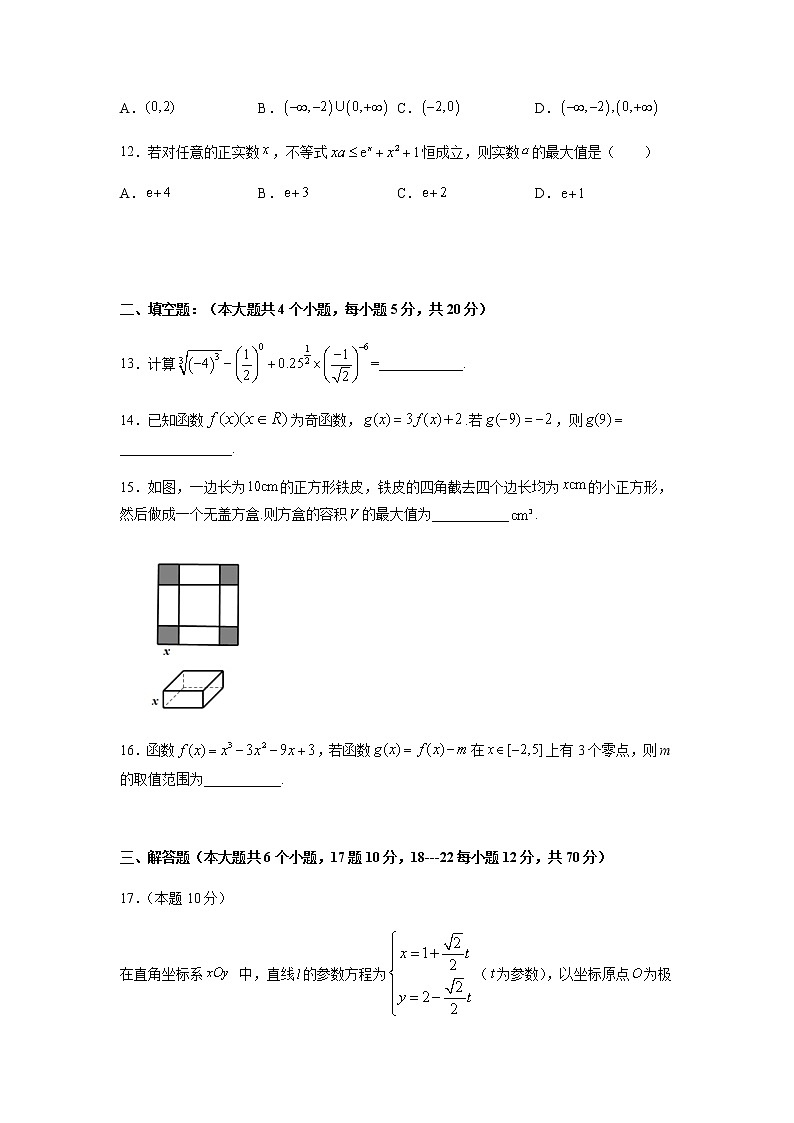
9．已知函数的导函数的图象如图所示，则关于函数的下列说法正确的是（    ）

A．在上为增函数 B．在处取得极大值

C．在上为增函数 D．在处取得极小值

10．在下列区间中，方程的解所在的区间为（    ）

A． B． C． D．

11．幂函数的图象过点，则函数的递增区间为（    ）

A． B． C． D．

12．若对任意的正实数，不等式恒成立，则实数的最大值是（    ）

A． B． C． D．

二、填空题：（本大题共4个小题，每小题5分，共20分）

13．计算=____________.

14．已知函数为奇函数，.若，则________________.

15．如图，一边长为的正方形铁皮，铁皮的四角截去四个边长均为的小正方形，然后做成一个无盖方盒.则方盒的容积的最大值为___________.

16．函数，若函数在上有3个零点，则m的取值范围为___________.

三、解答题（本大题共6个小题，17题10分，18---22每小题12分，共70分）

17．（本题10分）

在直角坐标系 中，直线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）写出直线的普通方程与曲线的直角坐标方程；

（2）求直线被曲线截得的弦长.

18．（本题12分）

已知在等差数列中，，．

（1）求数列的通项公式：

（2）设，求数列的前n项和．

19．（本题12分）

已知函数．

（1）求函数在点处的切线方程；

（2）求函数的单调区间及极值．

20．（本题12分）

在中，角A，B，C的对边分别是，且满足

（1）求角A．

（2）若边长，且的面积是，求边长b及c．

21．（本题12分）

已知函数.

（1）当时，求函数在区间上的值域；

（2）求函数在区间上的最大值.

22．（本题12分）

已知函数．

（1）若恒成立，求实数的取值范围．

（2）若函数的两个零点为，，证明：．

大庆中学2021--2022学年度上学期开学考

高三文科数学答案

一、选择题

1．D  2．C  3．C  4．B  5．B  6．A  7．A  8．B  9．C  10．B  11．D  12．C

二、填空题

13．    14．    15．   16．

三、解答题

17．解：（1）由直线的参数方程( t为参数可得其普通方程为：；

由曲线的极坐标方程得，所以曲线的直角坐标方程为：.

（2）由（1）得曲线：，圆心到直线的距离为：，

所以直线被曲线截得的弦长为：.

18．解：设等差数列的公差为，由，可得解得，

所以等差数列的通项公式可得;

（2） 由（1）可得，

所以.

19．（1）因为，所以，

∴切线方程为，即+1；

（2），所以当或时，，

当时，，所以函数的单调增区间是，单调减区间是和，极大值为，极小值为．

20．解：（1）在中，，

由正弦定理得，，

，，，因为 ，

（2），．，．

所以，即所以．

21．解:（1）由题意，当时，，又，对称轴为，，

离对称轴较远，，的值域为.

（2）由题意，二次函数开口向上，对称轴为，由数形结合知，

（i）当，即时，；

（ii）当，即时，，

综上：.

22．解:（1）解：因为恒成立，所以，即恒成立．

令，则，

易知在上单调递增，且．

所以当时，；当时，．

所以在上单调递减，在上单调递增，

所以，故．

（2）证明：由题意可知方程的两根为，．

令，则的两个零点为，．

．

当时，，在上单调递增，不存在两个零点；

当时，在上单调递增，在上单调递减，

则，得．

设，则，．

因为，所以，．

要证，即要证，即证．

令

，．

则，所以在上单调递减，所以．

因为，所以．

因为，，且在上单调递减，

所以，即，故成立．