2020-2021学年湖北省潜江市高二（上）10月月考数学试卷人教A版

这是一份2020-2021学年湖北省潜江市高二（上）10月月考数学试卷人教A版，共9页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。

1. 已知向量a→=1,2,−1，向量的模就是点0,0,0与点1,2,−1的距离，则|a→|=( )
A.1B.2C.2D.3

2. 直线3x−3y−5=0的倾斜角为( )
A.π6B.π3C.23πD.56π

3. 两平行直线 4x+3y−1=0，8x+6y+1=0的距离为( )
A.25B.310C.35D.15

4. 已知在直三棱柱ABC−A1B1C1中，底面是边长为2的正三角形，AA1=AB，则异面直线A1B与AC1所成角的余弦值为( )
A.−14B.14C.−154D.154

5. 已知直线l1:ax+y+1=0，l2:x+ay+1=0，若l1//l2，则实数a=( )
A.−1或1B.0或1C.1D.−1

6. 与直线3x−4y+5=0关于y轴对称的直线方程为( )
A.3x+4y+5=0B.3x+4y−5=0C.3x−4y+5=0D.3x−4y−5=0

7. 已知正三棱锥A−BCD 三条侧棱两两相互垂直且长为1，则其外接球的表面积为( )
A.3πB.4πC.8πD.12π

8. 已知直线l：4x+3y−10=0与圆C：x2+y2=r2r>0 相切，则r=( )
A.1B.2C.2D.5
二、多选题

已知直线l1：x+3y−3=0，l2：x−y+1=0，则( )
A.两直线相交于点0,1B.两直线夹角为 105∘
C.两直线夹角为15∘D.两直线夹角为75∘

下列叙述不正确的是( )
A.已知直线xsinα+2y−1=0与直线x−ycsα+3=0垂直，则tanα=2
B.若a→=x1,y1,b→=x2,y2，则a→⊥b→⇔x1x2+y1y2=0
C.不经过原点的直线都可以用方程xa+yb=1表示
D.经过定点A0,b的直线都可以用方程y=kx+b表示

已知圆C:x2+y2=4，动直线l:x+y−m=0，关于圆上的点到直线距离为1，以下结论正确的是( )
A.当m=0时有四个点B.当m=2时有三个点
C.当m=32时有一个点D.按m的不同有四种情况

一条光线从点A−2,3射出，经x轴反射后与圆C： x−32+y−22=1相切，则( )
A.入射光线与反射光线所在直线斜率之和为0
B.反射光线所在直线斜率为34或43
C.x轴上的反射点为2,0，14,0
D.反射光线过圆心时所在直线方程为x−y−1=0
三、填空题

已知直线x+my−m=0与2x−my+1=0垂直，则m=________.

已知点P3,1到直线l：x+ay−3=0的距离为12，则a=________.

已知点A2,3,B3,2，若直线l过点P1,1与线段AB相交，则直线l的斜率k的取值范围是________.

设动点P在棱长为1的正方体ABCD−A1B1C1D1的对角线BD1上，记D1PD1B=λ．当∠APC为钝角时，则λ的取值范围是________.
四、解答题

已知过原点的动直线l与圆C1:x2+y2−6x+5=0相交于不同的两点A，B．
(1)求圆C1的圆心坐标；

(2)求线段AB的中点M的轨迹C的方程．

在平面直角坐标系中，△ABC的三个顶点坐标分别为A(2, 1)，B(−2, 3)，C(−3, 0)，求：
(1)BC边所在直线的方程；

(2)BC边上的高AD所在直线的方程．

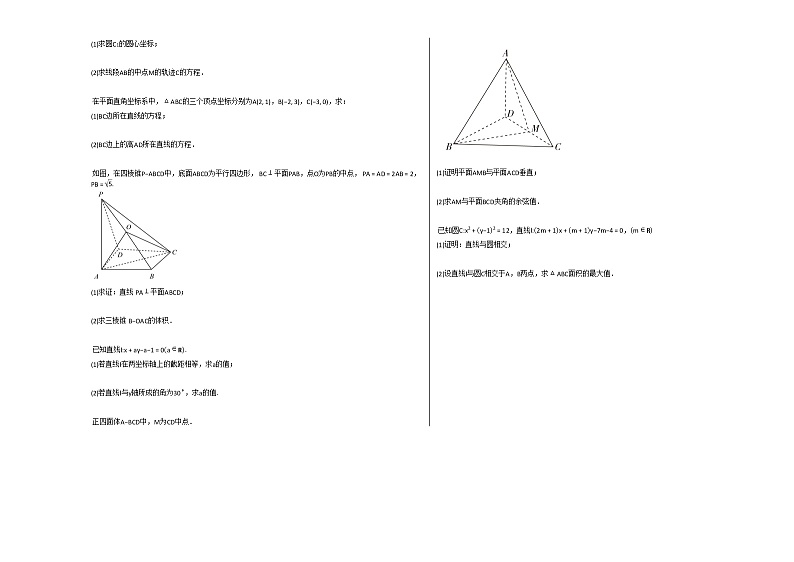
如图，在四棱锥P−ABCD中，底面ABCD为平行四边形， BC⊥平面PAB，点O为PB的中点， PA=AD=2AB=2，PB=5.

(1)求证：直线 PA⊥平面ABCD；

(2)求三棱锥 B−OAC的体积．

已知直线l:x+ay−a−1=0a∈R.
(1)若直线l在两坐标轴上的截距相等，求a的值；

(2)若直线l与y轴所成的角为30∘，求a的值.

正四面体A−BCD中，M为CD中点．

(1)证明平面AMB与平面ACD垂直；

(2)求AM与平面BCD夹角的余弦值．

已知圆C:x2+y−12=12，直线l:2m+1x+m+1y−7m−4=0，m∈R
(1)证明：直线与圆相交；

(2)设直线l与圆C相交于A，B两点，求△ABC面积的最大值．
参考答案与试题解析
2020-2021学年湖北省潜江市高二（上）10月月考数学试卷
一、选择题
1.
【答案】
B
【考点】
向量的模
【解析】
利用模长公式求解即可.
【解答】
解：由题意可得a→=12+22+−12=2.
故选B.
2.
【答案】
A
【考点】
直线的倾斜角
【解析】
求出直线的斜率，由直线的倾斜角与斜率的关系，计算即可得到所求值．
【解答】
解：直线3x−3y−5=0的斜率为k=33，
设直线的倾斜角为α，
可得tanα=33，
由0≤α0的圆心为原点，半径为r，
∴ 由直线4x+3y−10=0与圆C:x2+y2=r2r>0相切，
得到原点到直线的距离d=r，
即r=|4×0+3×0−10|42+32=2.
故选C．
二、多选题
【答案】
A,D
【考点】
两直线的夹角
两条直线的交点坐标
【解析】
解关于l1，l2的方程求得交点，直线l1的斜率k1=−33，直线l2的斜率k2=1，设两直线的夹角为θ，则tanθ=|k1−k21+k1k2|，由此能求出结果．
【解答】
解：联立两直线x+3y−3=0，x−y+1=0，
解得x=0，y=1，
∴ 两直线相交于点0,1，故A正确；
直线l1:x+3y−3=0的斜率k1=−33，
直线l2:x−y+1=0的斜率k2=1，
设两直线的夹角为θ，
则 tanθ=|k1−k21+k1k2|=|−33−1|1+(−33)×1|=2+3，
又0∘≤θ≤90∘，
∴ θ=75∘，
故BC错误，D正确．
故选AD．
【答案】
C,D
【考点】
命题的真假判断与应用
数量积判断两个平面向量的垂直关系
直线的截距式方程
直线的斜截式方程
两条直线垂直与倾斜角、斜率的关系
两条直线垂直的判定
【解析】
利用直线方程的定义，对选项逐项判定即可；
【解答】
解：对于A，∵ sinα与csα不能同时为0，
故两直线垂直，则斜率一定存在，
∴ csα≠0,
∵ 直线xsinα+2y−1=0与直线x−ycsα+3=0垂直，
∴ sinα−2cs α=0，解得tanα=2，故A正确；
对于B，显然成立；
对于C，不经过原点，且与坐标轴不垂直的直线都可以用方程 xa+yb=1表示，
故C不正确；
对于D，经过定点A0,b ，且斜率存在的直线都可以用方程y=kx+b表示，
故D不正确.
故选CD.
【答案】
A,B,C
【考点】
直线与圆的位置关系
点到直线的距离公式
【解析】
根据圆心到直线的距离和半径的关系,注意结合图形来分析与求解.
【解答】
解：因为圆心0,0到直线x+y−m=0的距离为
d=−m2=22|m|，圆的半径r=2，
所以当m=0时，d=0，直线l过圆心，A正确；
当m=2时，d=1，直线l过某条半径的中点，B正确；
当m=32时，d=3，直线l与圆相离，圆上的点到l的距离的最小值等于d−r=1，且这样的点是唯一的，C正确；
当m取不同的值时，圆上到直线l的距离等于1的点的个数可能为0，1，2，3，4，共有五种情况，D错误.
故选ABC.
【答案】
A,B,C
【考点】
直线与圆的位置关系
圆的切线方程
点到直线的距离公式
直线的点斜式方程
斜率的计算公式
【解析】
利用反射光线与入射光线的关系，结合对称性以及直线与圆相切等条件逐项判定求解.
【解答】
解：对于A，∵ 反射光线与入射光线对应的倾斜角互补，
∴ 斜率之和为0，A正确；
对于B，由题意可知：点−2,−3在反射光线上．
设反射光线所在的直线方程为：
y+3=kx+2，即kx−y+2k−3=0.
易知圆心坐标为3,2，半径是1，
由相切的性质可得： |3k−2+2k−3|k2+1=1，
化为： 12k2−25k+12=0，
解得k=34或43，B正确；
对于C，由B选项可得：
反射光线所在直线方程为4x−3y−1=0或3x−4y−6=0，
令y=0，可得反射点为2,0或14,0，C正确；
对于D，既然反射光线过圆心，那么就不可能与圆相切，故D错误.
故选ABC.
三、填空题
【答案】
±2
【考点】
直线的一般式方程与直线的垂直关系
【解析】
由直线x+my−m=0，2x−my+1=0垂直，知2×1+(−m)×m=0，由此能求出m的值．
【解答】
解：∵ 直线x+my−m=0与2x−my+1=0垂直，
∴ 2×1+(−m)×m=0，
解得m=±2．
故答案为：±2．
【答案】
±33
【考点】
点到直线的距离公式
【解析】
利用点到直线的距离公式求解即可.
【解答】
解：∵ 点P3,1到直线l：x+ay−3=0的距离为12，
∴ 3+a−312+a2=12，
解得a=±33.
故答案为：±33.
【答案】
12,2
【考点】
直线的图象特征与倾斜角、斜率的关系
斜率的计算公式
直线的斜率
【解析】
利用斜率公式求得斜率临界值，结合图像即可求解.
【解答】
解：如图，

kPA=3−12−1=2，kPB=2−13−1=12,
结合图象可知直线l的斜率k的取值范围为12≤k≤2.
故答案为：12,2.
【答案】
(13, 1)
【考点】
用空间向量求直线间的夹角、距离
空间向量的数量积运算
向量的几何表示
【解析】
本题考查利用向量法解题的意识.
【解答】
解：由题意，以DA→，DC→，DD1→为单位正交基底，
建立如图所示的空间直角坐标系D−xyz，
则有A(1, 0, 0)，B(1, 1, 0)，C(0, 1, 0)，D1(0, 0, 1)，
由D1B→=(1, 1, −1)，D1PD1B=λ，
得D1P→=λD1B→=(λ, λ, −λ)，
所以PA→=PD1→+D1A→
=(−λ, −λ, λ)+(1, 0, −1)=(1−λ, −λ, λ−1)，
PC→=PD1→+D1C→
=(−λ, −λ, λ)+(0, 1, −1)=(−λ, 1−λ, λ−1)，
显然∠APC不是平角，
所以∠APC为钝角等价于cs∠APC=cs=PA→⋅PC→|PA→||PC→|