2020-2021学年山东省高二（上）期中数学试卷人教A版

这是一份2020-2021学年山东省高二（上）期中数学试卷人教A版，共10页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。


1. 直线x−3y−1=0的倾斜角α=( )
A.30∘B.60∘C.120∘D.150∘

2. 过原点且倾斜角为60∘的直线被圆x2+y2−4y＝0所截得的弦长为（ ）

A.3B.2C.6D.23

3. 在四面体OABC中，E为OA中点，CF→=13CB→，若OA→=a→，OB→=b→，OC→=c→，则EF→=( )
A.12a→−13b→−23c→B.−12a→−13b→+43c→
C.−12a→+23b→+13c→D.−12a→+13b→+23c→

4. 设椭圆C1的离心率为513，焦点在x轴上且长轴长为26，若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8，则曲线C2的标准方程为( )
A.x242−y232=1B.x2132−y252=1
C.x232−y242=1D.x2132−y2122=1

5. 万众瞩目的北京冬奥会将于2022年2月4日正式开幕，继2008年北京奥运会之后，国家体育场（又名鸟巢）将再次承办奥运会开幕式．在手工课上，王老师带领同学们一起制作了一个近似鸟巢的金属模型，其俯视图可近似看成是两个大小不同，扁平程度相同的椭圆，已知大椭圆的长轴长为40cm，短轴长为20cm，小椭圆的短轴长为10cm，则小椭圆的长轴长为( )cm

A.30B.20C.10D.103

6. 设x，y∈R，向量a→=(x,1,1)，b→=(1, y, 1)，c→=(2, −4, 2)，且a→⊥c→，b→ // c→，则|a→+b→|=( )
A.22B.10C.3D.4

7. 已知双曲线x2a2−y2b2=1(a>0,b>0)的一条渐近线方程为x+3y＝0，则该双曲线的离心率是（ ）
A.103B.2C.73D.5

8. 在长方体ABCD−A1B1C1D1中，AB=BC=1，AA1=3，则异面直线AD1与DB1所成角的余弦值为（ ）
A.15B.56C.55D.22

9. 已知点A(2, 2)，B(−1, 3)，若直线kx−y−1＝0与线段AB有交点，则实数k的取值范围是（ ）
A.(−∞, −4)∪(32, +∞)B.(−4, 32)
C.(−∞, −4]∪[32, +∞)D.[−4, 32]

10. 正三棱锥P−ABC的侧面都是直角三角形，E，F分别是AB，BC的中点，则PB与平面PEF所成角的正弦为（ ）
A.36B.66C.33D.63
二、多项选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分）

圆O1:x2+y2−2x＝0和圆O2:x2+y2+2x−4y＝0的交点为A，B，则有（ ）
A.公共弦AB所在直线方程为x−y＝0
B.线段AB中垂线方程为x+y−1＝0
C.公共弦AB的长为22
D.P为圆O1上一动点，则P到直线AB距离的最大值为22+1

已知双曲线C过点(3, 2)且渐近线为y=±33x，则下列结论正确的是( )
A.双曲线C的方程为x23−y2=1
B.双曲线C的离心率为3
C.曲线y=ex−2−1经过C的一个焦点
D.直线x−2y−1=0与C有两个公共点

如图，设E，F分别是正方体ABCD−A1B1C1D1的棱DC上两点，且AB＝2，EF＝1，其中正确的命题为（ ）

A.三棱锥D1−B1EF的体积为定值
B.异面直线D1B1与EF所成的角为60∘
C.D1B1⊥平面B1EF
D.直线D1B1与平面B1EF所成的角为30∘

已知实数x，y满足方程x2+y2−4x+1＝0，则下列说法错误的是（ ）
A.y−x的最大值为6−2B.x2+y2的最大值为7+43
C.yx的最大值为32D.x+y的最大值为2+3
三、填空题（本题共4小题，每小题5分，共20分）

双曲线x2a2−y2b2=1的其中一条渐近线方程为y＝2x，且焦点到渐近线的距离为2，则双曲线的方程为________．

在棱长为2的正方体ABCD−A1B1C1D1中，E，F分别为棱AA1，BB1的中点，G为棱A1B1上的一点，且A1G＝λ(0<λ<2)，则点G到平面D1EF的距离为________．


若双曲线x2a2−y2b2=1(a>0, b>0)与直线y=3x无交点，则离心率e的取值范围是________．

已知圆C的圆心在直线x+y＝0上，圆C与直线x−y＝0相切，且在直线x−y−3＝0上截得的弦长为6，则圆C的方程为________．
四、解答题（本小题共5小题，共60分。解答应写出文字说明、证明过程或演算步骤）

若直线l的方程为ax+2y−a−2=0(a∈R)．
(1)若直线l与直线m:2x−y=0垂直，求a的值．

(2)若直线l在两轴上的截距相等，求该直线的方程．

已知双曲线C:x2a2−y2b2=1(a>0, b>0)与双曲线y26−x22=1的渐近线相同，且经过点(2, 3)．
（1）求双曲线C的方程；

（2）已知双曲线C的左右焦点分别为F1，F2，直线l经过F2，倾斜角为34π，l与双曲线C交于A，B两点，求△F1AB的面积．

在直角坐标系xOy中，已知圆C:x2+y2−4x−6y+m＝0与直线l:x+y−1＝0相切．
（1）求实数m的值；

（2）过点(3, 1)的直线与圆C交于M、N两点，如果|MN|＝23，求OM→⋅ON→．

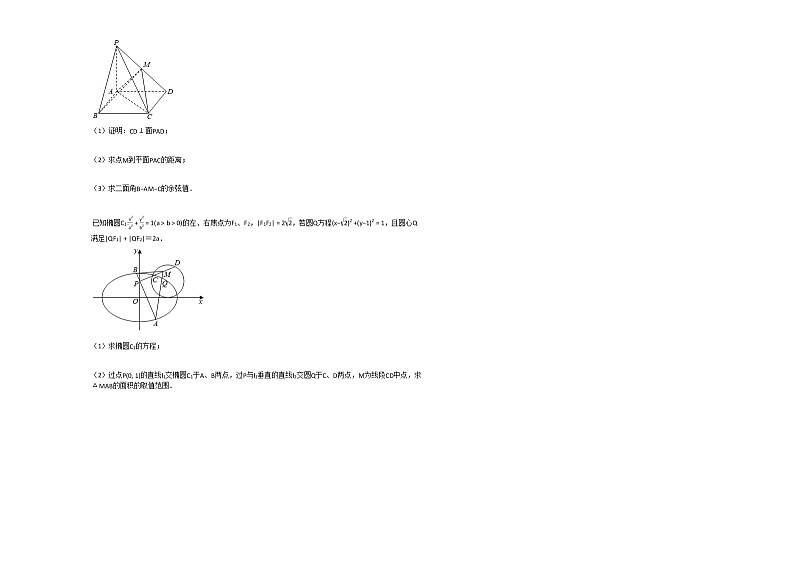
如图，在四棱锥P−ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA＝AD＝4，AB＝2，M是PD上一点，且BM⊥PD．

（1）证明：CD⊥面PAD；

（2）求点M到平面PAC的距离；

（3）求二面角B−AM−C的余弦值．

已知椭圆C1:x2a2+y2b2=1(a>b>0)的左、右焦点为F1、F2，|F1F2|=22，若圆Q方程(x−2)2+(y−1)2=1，且圆心Q满足|QF1|+|QF2|＝2a．

（1）求椭圆C1的方程；

（2）过点P(0, 1)的直线l1交椭圆C1于A、B两点，过P与l1垂直的直线l2交圆Q于C、D两点，M为线段CD中点，求△MAB的面积的取值范围．
参考答案与试题解析
2020-2021学年山东省高二（上）期中数学试卷
一、单项选择题（本题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求）
1.
【答案】
A
【考点】
直线的倾斜角
直线的图象特征与倾斜角、斜率的关系
【解析】
由直线方程可得直线的斜率，再由斜率和倾斜角的关系可得所求．
【解答】
解：可得直线x−3y−1=0的斜率为k=13=33，
由斜率和倾斜角的关系可得tanα=33.
又∵ 0∘≤α≤180∘，
∴ α=30∘.
故选A.
2.
【答案】
D
【考点】
直线和圆的方程的应用
【解析】
本题考查的知识点是直线与圆方程的应用，由已知圆x2+y2−4y＝0，我们可以将其转化为标准方程的形式，求出圆心坐标和半径，又直线由过原点且倾斜角为60∘，得到直线的方程，再结合半径、半弦长、弦心距满足勾股定理，即可求解．
【解答】
将圆x2+y2−4y＝0的方程可以转化为：
x2+(y−2)2＝4，
即圆的圆心为A(0, 2)，半径为R＝2，
∴ A到直线ON的距离，即弦心距为1，
∴ ON=3，
∴ 弦长23，
3.
【答案】
D
【考点】
平面向量的基本定理
【解析】
利用向量的加减法，及线性运算，即可得出结论．
【解答】
由题意，EF→=EA→+AB→+BF→=12a→+b→−a→+13(c→−b→)=−12a→+13b→+23c→．
4.
【答案】
A
【考点】
双曲线的标准方程
椭圆的定义
【解析】
在椭圆C1中，由题设条件能够得到a=13c=5，曲线C2是以F1(−5, 0)，F2(5, 0)，为焦点，实轴长为8的双曲线，由此可求出曲线C2的标准方程．
【解答】
解：在椭圆C1中，由2a=26,ca=513,
得a=13,c=5.
椭圆C1的焦点为F1(−5, 0)，F2(5, 0)，
曲线C2是以F1、F2为焦点，实轴长为8的双曲线，
故C2的标准方程为：x242−y232=1.
故选A．
5.
【答案】
B
【考点】
椭圆的离心率
【解析】
求出大椭圆的离心率等于小椭圆的离心率，然后求解小椭圆的长轴长．
【解答】
因为两个椭圆的扁平程度相同，所以椭圆的离心率相同，
所以两个椭圆的离心率相同，
所以2a2b=2a2b，
所以4020=2a10，
所以小椭圆的长轴长为：20cm．
6.
【答案】
C
【考点】
向量的数量积判断向量的共线与垂直
向量的模
【解析】
利用向量平行和向量垂直的性质列出方程组，求出x，y，再由平面向量坐标运算法则求出a→+b→，由此能求出|a→+b→|．
【解答】
解：由题意知，x，y∈R，向量a→=(x, 1, 1)，b→=(1, y, 1)，c→=(2, −4, 2)，
且a→⊥c→，b→ // c→，
∴ 2x−4+2=0，12=y−4=12，
解得x=1，y=−2，
∴ a→+b→=(1, 1, 1)+(1, −2, 1)=(2, −1, 2)，
∴ |a→+b→|=4+1+4=3．
故选C.
7.
【答案】
A
【考点】
双曲线的离心率
【解析】
由题意设出双曲线的方程，得到它的一条渐近线方程y=bax即y=−13x，由此可得b:a＝1:3，结合双曲线的平方关系可得c与a的比值，求出该双曲线的离心率．
【解答】
∵ 双曲线的中心在原点，焦点在x轴上，
∴ 设双曲线的方程为 x2a2−y2b2=1(a>0,b>0)，由此可得双曲线的渐近线方程为y＝±bax，结合题意一条渐近线方程为y=−13x，得 ba=13，
设a＝3t，b＝t，则c=a2+b2=10t(t>0)
∴ 该双曲线的离心率是e=ca=103，
8.
【答案】
C
【考点】
异面直线及其所成的角
【解析】
以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出异面直线AD1与DB1所成角的余弦值．
【解答】
解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，
建立空间直角坐标系，
∵ 在长方体ABCD−A1B1C1D1中，
AB=BC=1，AA1=3，
∴ A(1, 0, 0)，D1(0, 0, 3)，
D(0, 0, 0)，B1(1, 1, 3)，
∴ AD1→=(−1, 0, 3)，DB1→=(1, 1, 3)，
设异面直线AD1与DB1所成角为θ，
则csθ=AD→1⋅DB→1|AD→1|⋅|DB1→|=225=55，
∴ 异面直线AD1与DB1所成角的余弦值为55．
故选C．
9.
【答案】
C
【考点】
两条直线的交点坐标
【解析】
根据题意知A、B两点在直线的异侧或在直线上，
得出不等式(2k−2−1)×(−k−3−1)≤0，求出解集即可．
【解答】
根据题意，若直线l:kx−y−1＝0与线段AB相交，
则A、B在直线的异侧或在直线上，
则有(2k−2−1)×(−k−3−1)≤0，
即(2k−3)(k+4)≥0，
解得k≤−4或k≥32，
即k的取值范围是(−∞, −4]∪[32, +∞)．
10.
【答案】
C
【考点】
直线与平面所成的角
【解析】
以P为原点，PA为x轴，PB为y轴，PC为z轴，建立空间直角坐标系，利用向量法能求出PB与平面PEF所成角的正弦值．
【解答】
∵ 正三棱锥P−ABC的侧面都是直角三角形，E，F分别是AB，BC的中点，
∴ 以P为原点，PA为x轴，PB为y轴，PC为z轴，建立空间直角坐标系，
设PA＝PB＝PC＝2，
则A(2, 0, 0)，B(0, 2, 0)，C(0, 0, 2)，E(1, 1, 0)，F(0, 1, 1)，
PB→=(0, 2, 0)，PE→=(1, 1, 0)，PF→=(0, 1, 1)，
设平面PEF的法向量n→=(x, y, z)，
则n→⋅PE→=x+y=0n→⋅PF→=y+z=0 ，取x＝1，得n→=(1, −1, 1)，
设PB与平面PEF所成角为θ，
则sinθ=|PB→⋅n→||PB→|⋅|n→|=223=33．
∴ PB与平面PEF所成角的正弦值为33．
二、多项选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分）
【答案】
A,B,D
【考点】
圆与圆的位置关系及其判定
【解析】
两圆 的方程作差即可求出公共弦的直线方程，即可判断选项A；求出两圆圆心坐标，即可求出线段AB的中垂线的方程，即可判断选项B．
求出圆心O1到直线AB的距离d，d+r即为圆O1上的点到直线AB的最大值，利用垂径定理求出公共弦长，即可判断选项CD．
【解答】
∵ 圆O1:x2+y2−2x＝0和圆O2:x2+y2+2x−4y＝0的交点为A，B，
∴ 圆O1与圆O2公共弦AB所在的直线方程为x−y＝0，故A正确；
∵ O1(1, 0)，O2(−1, 2)，O1O2所在直线斜率为−1，
∴ 线段AB的中垂线的方程为y−0＝−(x−1)，即x+y−1＝0，故B正确；
圆O1:x2+y2−2x＝0的圆心为O1(1, 0)，半径r1＝1，
圆心O1(1, 0)到直线x−y＝0的距离d=12=22．
∴ P到直线AB距离的最大值为22+1，
圆O1与圆O2公共弦AB的长为21−12=2，故C错误，D正确．
【答案】
A,C
【考点】
双曲线的离心率
双曲线的渐近线
双曲线的标准方程
【解析】
根据条件可求出双曲线C的方程，再逐一排除即可．
【解答】
解：设双曲线C的方程为x2a2−y2b2=1，
根据条件可知ba=33，所以方程可化为x23b2−y2b2=1，
将点(3, 2)代入得b2=1，所以a2=3，
所以双曲线C的方程为x23−y2=1，故A对；
离心率e=ca=a2+b2a2=3+13=233，故B错；
双曲线C的焦点为(2, 0)，(−2, 0)，
将x=2代入得y=e0−1=0，所以C对；
联立x23−y2=1，x−2y−1=0， 整理得y2−22y+2=0，
则Δ=8−8=0，故只有一个公共点，故D错.
故选AC.
【答案】
A,B,D
【考点】
命题的真假判断与应用
【解析】
根据题意画出图形，结合图形求出三棱锥D1−B1EF的体积为定值，可判断选项A；
求得异面直线D1B1与EF所成的角为45∘可判断B；
判断D1B1与平面B1EF不垂直可判断C；
直线D1B1与平面B1EF所成的角是为30∘可判断D．
【解答】
如图所示，
三棱锥D1−B1EF的体积为V=13S△D1EF⋅B1C1=13×12×2×2×1=23为定值，A正确；
EF // D1C1，∠B1D1C1是异面直线D1B1与EF所成的角，为45∘，B正确；
D1B1与EF不垂直，由此知D1B1与平面B1EF不垂直，C错误；
在三棱锥D1B1DC中，设D1到平面DCB1的距离为ℎ，
VB1−D1DC=VD1−DCB1，即有13×2×12×2×2=13×12×2×22ℎ，解得ℎ=2，
直线D1B1与平面B1EF所成的角的正弦为222=12，即直线D1B1与平面B1EF所成的角为30∘，D正确．
综上，正确的命题为ABD．
【答案】
C,D
【考点】
直线与圆的位置关系
圆的一般方程
【解析】
令s＝y−x，化为直线的一般方程，利用圆心到直线的距离小于等于半径求得s的范围判断A；同理判断D；求出圆上的点到原点距离平方的最大值判断B；求出过原点且与圆有交点的直线的斜率的最大值判断C．
【解答】
由x2+y2−4x+1＝0，得(x−2)2+y2＝3，
令s＝y−x，即x−y+s＝0，由|2+s|2≤3，解得−6−2≤s≤6−2，
∴ y−x的最大值为6−2，故A正确；
圆心(2, 0)到原点的距离为2，则圆上的点到原点的距离的最大值为2+3，
可得x2+y2的最大值为(2+3)2=7+43，故B正确；
设过原点的直线的斜率为k，直线方程为y＝kx，由|2k|k2+1≤3，
解得−3≤k≤3，即yx的最大值为3，故C错误；
令t＝x+y，即x+y−t＝0，由|2−t|2≤3，解得2−6≤t≤2+6，
则x+y的最大值为2+6，故D错误．
三、填空题（本题共4小题，每小题5分，共20分）
【答案】
x2−y24=1
【考点】
双曲线的标准方程
双曲线的离心率
【解析】
先根据双曲线的焦点坐标，求得a和b的关系，进而代入焦点到渐近线的距离，求得a和b，则双曲线的渐近线方程可得．
【解答】
∵ 双曲线的一条渐近线方程是y＝2x，
∴ b＝2a，
又∵ 焦点到渐近线的距离为 2，
∴ b＝2
∴ a＝1，
∴ 双曲线方程为x2−y24=1．
【答案】
255
【考点】
点、线、面间的距离计算
【解析】
以D为原点，DA，DC，DD1所在直线分别为x轴，y轴，z轴建立空间直角坐标系D−xyz，利用向量法能求出点G到平面D1EF的距离．
【解答】
以D为原点，DA，DC，DD1所在直线分别为x轴，y轴，z轴建立空间直角坐标系D−xyz，
则G(2, λ, 2)，D1(0, 0, 2)，E(2, 0, 1)，F(2, 2, 1)，
所以D1E→=(2,0,−1)，D1F→=(2,2,−1)，GE→=(0,−λ,−1)，
设平面D1EF的法向量为n→=(x,y,z)，则2x−z=0,2x+2y−z=0,
令x＝1，则y＝0，z＝2，所以平面D1EF的一个法向量n→=(1,0,2)．
点G到平面D1EF的距离为|GE→⋅n→|n→||=|−1×25|=255．
【答案】
(1, 2]
【考点】
双曲线的离心率
直线与椭圆结合的最值问题
【解析】
双曲线x2a2−y2b2=1(a>0, b>0)与直线y=3x无交点，取双曲线的渐近线y=bax，则必有ba≤3，再利用离心率计算公式1【解答】
∵ 双曲线x2a2−y2b2=1(a>0, b>0)与直线y=3x无交点，取双曲线的渐近线y=bax．
∴ ba≤3，
∴ 1∴ 双曲线离心率e的取值范围是(1, 2]．
【答案】
(x−1)2+(y+1)2＝2
【考点】
直线与圆的位置关系
【解析】
设圆心为C(a, b)，半径为r，由题意可得关于a，b，r的方程组，求解可得a，b，r的值，则圆的方程可求．
【解答】
设圆心为C(a, b)，半径为r，
由题意可得，a+b=0r=|a−b|2(a−b−3|2)2+(62)2=r2 ，解得a=1b=−1r=2 ．
∴ 圆C的方程为(x−1)2+(y+1)2＝2．
四、解答题（本小题共5小题，共60分。解答应写出文字说明、证明过程或演算步骤）
【答案】
解：(1)∵ 直线l与直线m:2x−y=0垂直，
∴ 2a−2=0，解得a=1．
(2)当a=0时，直线l化为：y=1，不满足题意．
当a≠0时，可得直线l与坐标轴的交点(0, a+22)，(a+2a, 0)．
∵ 直线l在两轴上的截距相等，∴ a+22=a+2a，解得：a=±2．
∴ 该直线的方程为：x−y=0或x+y−2=0．
【考点】
两条直线垂直的判定
直线的截距式方程
【解析】
（1）直线l与直线m:2x−y＝0垂直，可得2a−2＝0，解得a．
（2）当a＝0时，直线l化为：y＝1．不满足题意．当a≠0时，可得直线l与坐标轴的交点(0, a+22)，(a+2a, 0)．根据直线l在两轴上的截距相等，即可得出．
【解答】
解：(1)∵ 直线l与直线m:2x−y=0垂直，
∴ 2a−2=0，解得a=1．
(2)当a=0时，直线l化为：y=1，不满足题意．
当a≠0时，可得直线l与坐标轴的交点(0, a+22)，(a+2a, 0)．
∵ 直线l在两轴上的截距相等，∴ a+22=a+2a，解得：a=±2．
∴ 该直线的方程为：x−y=0或x+y−2=0．
【答案】
设所求双曲线C的方程为y26−x22=λ(λ≠0, λ≠1)，
代入点(2, 3)得96−222=λ，
即λ=−12，所以双曲线C方程为y26−x22=−12，即x2−y23=1；
F1(−2, 0)，F2(2, 0)．直线AB的方程为y＝2−x．
设A(x1, y1)，B(x2, y2)，联立直线y＝2−x和椭圆方程3x2−y2＝3，
得2x2+4x−7＝0，满足△＝16+56>0，
x1+x2＝−2，x1x2=−72，
由弦长公式得|AB|=1+1⋅4−4⋅(−72)=6，
点F1(−2, 0)到直线AB:x+y−2＝0的距离d=|−2+0−2|2=22，
所以S​△F1AB=12|AB|d=12⋅6⋅22=62．
【考点】
双曲线的离心率
【解析】
（1）设所求双曲线C的方程为y26−x22=λ(λ≠0, λ≠1)，代入点(2, 3)，计算可得所求方程；
（2）求得两焦点的坐标，设出直线AB的方程，联立双曲线方程，运用韦达定理和弦长公式，以及点到直线的距离公式，三角形的面积公式，计算可得所求值．
【解答】
设所求双曲线C的方程为y26−x22=λ(λ≠0, λ≠1)，
代入点(2, 3)得96−222=λ，
即λ=−12，所以双曲线C方程为y26−x22=−12，即x2−y23=1；
F1(−2, 0)，F2(2, 0)．直线AB的方程为y＝2−x．
设A(x1, y1)，B(x2, y2)，联立直线y＝2−x和椭圆方程3x2−y2＝3，
得2x2+4x−7＝0，满足△＝16+56>0，
x1+x2＝−2，x1x2=−72，
由弦长公式得|AB|=1+1⋅4−4⋅(−72)=6，
点F1(−2, 0)到直线AB:x+y−2＝0的距离d=|−2+0−2|2=22，
所以S​△F1AB=12|AB|d=12⋅6⋅22=62．
【答案】
由x2+y2−4x−6y+m＝0可得(x−2)2+(y−3)2＝13−m．
由直线x+y−1＝0与圆相切可得，|2+3−1|2=13−m，
解可得，m＝5，
(i)当直线的斜率不存在时，直线方程x＝3，此时MN＝27，不合题意，
(ii)当直线的斜率存在时，可知MN所在的直线方程为y−1＝k(x−3)即kx−y+1−3k＝0，
圆心(2, 3)到MN的距离d=|2k−3+1−3k|1+k2=|k+2|1+k2，
根据直线与圆相交的性质可得，23=28−(k+2)21+k2，
解可得，k=12，此时直线方程x−2y−1＝0，
联立(x−2)2+(y−3)2=8x−2y−1=0 可得5y2−10y+2＝0，
设M(x1, y1)，N(x2, y2)，则y1+y2＝2，y1y2=25，
∴ x1x2＝(1+2y1)(1+2y2)＝1+2(y1+y2)+4y1y2=335，
∴ OM→⋅ON→=x1x2+y1y2＝7．
【考点】
圆的切线方程
平面向量数量积的性质及其运算
【解析】
（1）由已知结合直线与圆相切性质即可求解m，
（2）根据直线与圆相交性质及向量数量积的坐标表示即可求解．
【解答】
由x2+y2−4x−6y+m＝0可得(x−2)2+(y−3)2＝13−m．
由直线x+y−1＝0与圆相切可得，|2+3−1|2=13−m，
解可得，m＝5，
(i)当直线的斜率不存在时，直线方程x＝3，此时MN＝27，不合题意，
(ii)当直线的斜率存在时，可知MN所在的直线方程为y−1＝k(x−3)即kx−y+1−3k＝0，
圆心(2, 3)到MN的距离d=|2k−3+1−3k|1+k2=|k+2|1+k2，
根据直线与圆相交的性质可得，23=28−(k+2)21+k2，
解可得，k=12，此时直线方程x−2y−1＝0，
联立(x−2)2+(y−3)2=8x−2y−1=0 可得5y2−10y+2＝0，
设M(x1, y1)，N(x2, y2)，则y1+y2＝2，y1y2=25，
∴ x1x2＝(1+2y1)(1+2y2)＝1+2(y1+y2)+4y1y2=335，
∴ OM→⋅ON→=x1x2+y1y2＝7．
【答案】
证明：∵ PA⊥平面ABCD，PA⊂平面PAD，∴ 平面PAD⊥平面ABCD，
∵ 底面ABCD是矩形，∴ CD⊥AD，
又CD⊂平面ABCD，平面PAD∩平面ABCD＝AD
∴ CD⊥面PAD；
由（1）知，平面PAD⊥平面ABCD，
∵ 底面ABCD是矩形，∴ BA⊥AD，
又BA⊂平面ABCD，平面PAD∩平面ABCD＝AD，
∴ BA⊥面PAD，则BA⊥PD，
又BM⊥PD，BA∩BM＝B，∴ PD⊥平面ABM，则PD⊥AM，
∵ PA＝AD，则M为PD的中点，
∴ VM−PAC=12VP−ACD=12×13×12×4×2×4=83，
又S△PAC=12×42+22×4=45，
设点M到平面PAC的距离为ℎ，则13S△PAC×ℎ=13×45×ℎ=83，
解得ℎ=255；
以A为原点建立空间直角坐标系
【考点】
直线与平面垂直
点、线、面间的距离计算
二面角的平面角及求法
【解析】
（1）由PA⊥平面ABCD，得平面PAD⊥平面ABCD，结合底面ABCD是矩形，可得CD⊥面PAD；
（2）由（1）知，平面PAD⊥平面ABCD，得到BA⊥PD，再由已知BM⊥PD，可得PD⊥平面ABM，即PD⊥AM，进一步得到M为PD的中点，再由等体积法求M到平面PAC的距离；
（3）以A为原点建立空间直角坐标系，分别求出平面BAM与平面CAM的一个法向量，由两法向量所成角的余弦值可得二面角B−AM−C的余弦值．
【解答】
证明：∵ PA⊥平面ABCD，PA⊂平面PAD，∴ 平面PAD⊥平面ABCD，
∵ 底面ABCD是矩形，∴ CD⊥AD，
又CD⊂平面ABCD，平面PAD∩平面ABCD＝AD
∴ CD⊥面PAD；
由（1）知，平面PAD⊥平面ABCD，
∵ 底面ABCD是矩形，∴ BA⊥AD，
又BA⊂平面ABCD，平面PAD∩平面ABCD＝AD，
∴ BA⊥面PAD，则BA⊥PD，
又BM⊥PD，BA∩BM＝B，∴ PD⊥平面ABM，则PD⊥AM，
∵ PA＝AD，则M为PD的中点，
∴ VM−PAC=12VP−ACD=12×13×12×4×2×4=83，
又S△PAC=12×42+22×4=45，
设点M到平面PAC的距离为ℎ，则13S△PAC×ℎ=13×45×ℎ=83，
解得ℎ=255；
以A为原点建立空间直角坐标系
【答案】
由已知可得c=2，且F1(−2, 0)，F2(2, 0)，
圆Q的圆心Q(2, 1)，所以|QF1|+|QF2|＝3+1＝4＝2a，
所以a＝2，则b2＝a2−c2＝4−2＝2，
所以椭圆C1的方程为：x24+y22=1；
当l1平行于x轴时，l2与圆Q无公共点，从而三角形MAB不存在，
故可设l1:x＝t(y−1)，l2:tx+y−1＝0，
由x24+y22=1x=t(y−1) ，消去x整理可得：(t2+2)y2−2t2y+t2−4＝0，
设A(x1, y1)，B(x2, y2)，由韦达定理可得：y1+y2=2t2t2+2y1y2=t2−4t2+2 ，
则|AB|=1+t2|y1−y2|=1+t2⋅(y1+y2)2−4y1y2=2(1+t2)(2t2+8)t2+2，
又圆心Q(2, 1)到直线l2的距离为d2=|2−t+t|1+t2=21+t2，
所以三角形MAB的面积为S=12|AB|⋅d2=2t2+4t2+2，
令u=t2+4∈[2, 5)，则S＝f(u)=2uu2−2=2u−2u，
因为u−2u在区间[2, 5)上单调递增，所以u−2u∈[1, 355)，
所以2u−2u∈(253,2]，
所以三角形MAB的面积的取值范围为(253,2]．
【考点】
椭圆的应用
椭圆的标准方程
直线与椭圆的位置关系
椭圆的离心率
【解析】
（1）利用椭圆的焦点坐标以及圆心Q满足的关系式即可求出椭圆方程；
（2）先分析可得直线l1与x轴不可能平行，然后设出直线l1，l2的方程，联立椭圆方程和l1的方程，由韦达定理得出坐标关系，利用弦长公式求出|AB|的长度，
再求出圆心Q到直线l2的距离，进而可以求出三角形MAB的面积表达式，再利用函数的性质求出范围即可．
【解答】
由已知可得c=2，且F1(−2, 0)，F2(2, 0)，
圆Q的圆心Q(2, 1)，所以|QF1|+|QF2|＝3+1＝4＝2a，
所以a＝2，则b2＝a2−c2＝4−2＝2，
所以椭圆C1的方程为：x24+y22=1；
当l1平行于x轴时，l2与圆Q无公共点，从而三角形MAB不存在，
故可设l1:x＝t(y−1)，l2:tx+y−1＝0，
由x24+y22=1x=t(y−1) ，消去x整理可得：(t2+2)y2−2t2y+t2−4＝0，
设A(x1, y1)，B(x2, y2)，由韦达定理可得：y1+y2=2t2t2+2y1y2=t2−4t2+2 ，
则|AB|=1+t2|y1−y2|=1+t2⋅(y1+y2)2−4y1y2=2(1+t2)(2t2+8)t2+2，
又圆心Q(2, 1)到直线l2的距离为d2=|2−t+t|1+t2=21+t2，
所以三角形MAB的面积为S=12|AB|⋅d2=2t2+4t2+2，
令u=t2+4∈[2, 5)，则S＝f(u)=2uu2−2=2u−2u，
因为u−2u在区间[2, 5)上单调递增，所以u−2u∈[1, 355)，
所以2u−2u∈(253,2]，
所以三角形MAB的面积的取值范围为(253,2]．