

2020-2021学年山东省淄博市高二(上)期末数学试卷人教A版
展开1. 直线x+3y+1=0的倾斜角为( )
A.30∘B.60∘C.120∘D.150∘
2. 椭圆x2+2y2=1的焦点坐标是( )
A.(±1, 0)B.(0, ±1)C.(±,0)D.(0,±)
3. 空间两点A(1, 5, 4),B(−1, 3, 5)间的距离等于( )
A.2B.3C.4D.9
4. 圆C1:x2+y2+8x+12=0和圆C2:x2+y2−6y=0的位置关系是( )
A.相离B.相交C.内切D.外切
5. 2020年10月26日至29日,中国共产党第十九届中央委员会第五次全体会议在北京举行,审议通过了《中共中央关于制定国民经济和社会发展第十四个五年规划和二O三五年远景目标的建议》.某班级从3名男生和3名女生中任选2人参加学校十九届五中全会精神宣讲团,则选中的2人恰好都是女生的概率为( )
A.0.2B.0.3C.0.4D.0.5
6. 如图所示,在正方体ABCD−A1B1C1D1中,点F是侧面CDD1C1的中心,若=x+y+z,求x+y+z=( )
A.1B.C.2D.
7. 光线通过点A(2, 3),在直线l:x+y+1=0上反射,反射光线经过点B(1, 1),则反射光线所在直线方程为( )
A.4x−5y+1=0B.4x+5y−9=0C.5x−4y−1=0D.5x+4y−9=0
8. 设F1,F2是双曲线C:=1(a>0, b>0)的左、右焦点,P是双曲线C右支上一点.若|PF1|+|PF2|=6a,且=,则双曲线C的渐近线方程是( )
A.x±y=0B.xy=0C.x±2y=0D.2xy=0
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
若a→=(−1,λ,−2),b→=(2,−1,1),a→与b→的夹角为120∘,则λ的值为( )
A.17B.−17C.−1D.1
已知空间向量都是单位向量,且两两垂直,则下列结论正确的是( )
A.向量的模是3
B.可以构成空间的一个基底
C.向量和夹角的余弦值为
D.向量与共线
已知A,B是随机事件,则下列结论正确的是( )
A.若A,B是互斥事件,则P(AB)=P(A)P(B)
B.若事件A,B相互独立,则P(A+B)=P(A)+P(B)
C.若A,B是对立事件,则A,B是互斥事件
D.事件A,B至少有一个发生的概率不小于A,B恰好有一个发生的概率
已知F1,F2分别为双曲线=1(a>0, b>0)的左、右焦点,A1,A2分别为其实轴的左、右端点,且|F1F2|=,点P为双曲线右支一点,I为△PF1F2的内心,则下列结论正确的有( )
A.离心率
B.点I的横坐标为定值a
C.若(λ∈R)成立,则λ=−1
D.若PH垂直x轴于点H,则|PH|2=|HA1|⋅|HA2|
三、填空题:本题共4小题,每小题5分,共20分.
已知直线l1:(m−1)x−3y+3=0和直线l2:2x+my−5=0垂直,则实数m=________.
现有3个灯泡并联而成的闭合电路,如果在某段时间内每个灯泡能正常照明的概率都是0.9,那么在这段时间内该电路上的灯泡至少有两个能正常照明的概率是________.
已知空间直线l的方向向量是,平面α的法向量.若l⊥α,则a+b=________.
已知抛物线的焦点为F,过F的直线l与抛物线交于A,B两点,抛物线的准线与y轴交于点M,当最大时,弦AB长度是________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
已知在空间直角坐标系Oxyz中,点A,B,C,M的坐标分别是(2, 0, 2),(2, 1, 0),(0, 4, −1),(2, 3, −1),过点A,B,C的平面记为α.
(1)证明:点A,B,C,M不共面;
(2)求点M到平面α的距离.
已知△ABC中,点A(−1, 5),边BC所在直线l1的方程为7x−y−18=0,边AB上的中线所在直线l2的方程为y=x.
(1)求点B和点C的坐标;
(2)若△ABC的外接圆为⊙M,求直线l2被⊙M截得的弦长.
袋中有9个大小相同颜色不全相同的小球,分别为黑球、黄球、绿球,从中任意取一球,得到黑球或黄球的概率是59,得到黄球或绿球的概率是23,试求:
(I)从中任取一球,得到黑球、黄球、绿球的概率各是多少?
(II)从中任取两个球,得到的两个球颜色不相同的概率是多少?
在平面直角坐标系中,动点P(x, y)(y>0)到定点M(0, 1)的距离比到x轴的距离大1.
(1)求动点P的轨迹C的方程;
(2)过点M的直线l交曲线C于A,B两点,若|AB|=8,求直线l的方程.
如图所示,已知正方体ABCD−A1B1C1D1的棱长为2,E,F分别为BC,CD的中点.
(1)求平面C1EF与平面AB1D1夹角的余弦值;
(2)设,若平面C1EF // 平面MB1D1,求λ的值.
已知椭圆C:=1(a>b>0),四点P1(1, 1),P2(0, 1),P3(−1,),中恰有三点在椭圆C上.
(1)求椭圆C的方程;
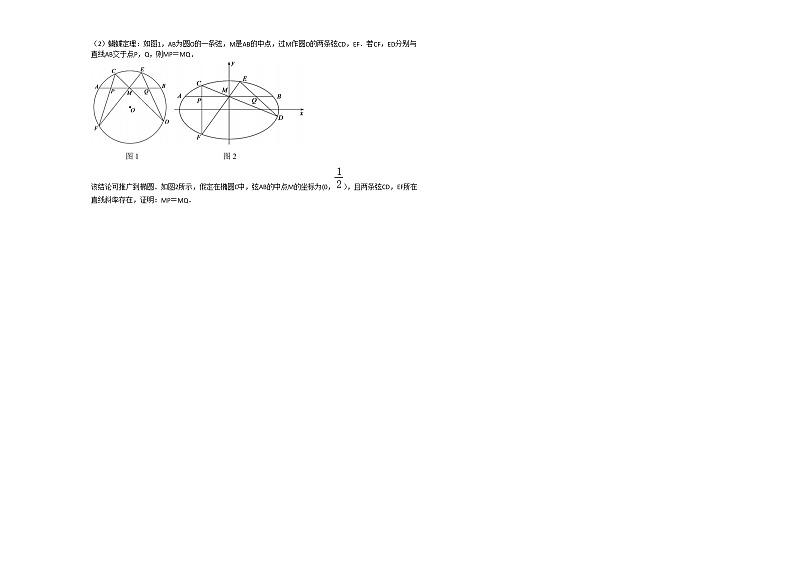
(2)蝴蝶定理:如图1,AB为圆O的一条弦,M是AB的中点,过M作圆O的两条弦CD,EF.若CF,ED分别与直线AB交于点P,Q,则MP=MQ.
该结论可推广到椭圆.如图2所示,假定在椭圆C中,弦AB的中点M的坐标为(0,),且两条弦CD,EF所在直线斜率存在,证明:MP=MQ.
参考答案与试题解析
2020-2021学年山东省淄博市高二(上)期末数学试卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】
D
【考点】
直线的倾斜角
【解析】
由直线方程求得直线的斜率,再由斜率等于倾斜角的正切值求解.
【解答】
解:直线x+3y+1=0的斜率k=−13=−33,
设其倾斜角为θ(0∘≤θ<180∘),
则tanθ=−33,
∴ θ=150∘.
故选D.
2.
【答案】
C
【考点】
椭圆的离心率
【解析】
依题意,可求得该椭圆的标准方程,从而可求其焦点坐标.
【解答】
∵ 椭圆x2+8y2=1的标准方程为:x2+=1,
∴ a2=1,b2=,
∴ c2=a2−b2=,
∴ c=.
又椭圆x2+2y2=1的焦点在x轴,
∴ 椭圆x2+2y2=1的焦点坐标是(±,0).
3.
【答案】
B
【考点】
空间两点间的距离公式
【解析】
直接利用两点间的距离公式进行求解,即可得到答案.
【解答】
因为空间两点A(1, 5, 4),B(−1, 3, 5),
故A,B两点间的距离为.
4.
【答案】
D
【考点】
圆与圆的位置关系及其判定
【解析】
根据题意,将两个圆的方程变形为标准方程,求出两个圆的圆心和半径,由圆心坐标求出圆心距,可得答案.
【解答】
根据题意圆C1:x2+y2+8x+12=0,即(x+4)2+y2=4,其圆心为(−4, 0),半径r=2,
圆C2:x2+y2−6y=0,即x2+(y−3)2=9,其圆心为(0, 3),半径R=3,
圆心距|C1C2|==5,
则圆心距|C1C2|=R+r=5,则两圆外切,
5.
【答案】
A
【考点】
古典概型及其概率计算公式
【解析】
基本事件总数n==15,选中的2人恰好都是女生包含的基本事件个数m==3,由此能求出选中的2人恰好都是女生的概率.
【解答】
某班级从3名男生和3名女生中任选6人参加学校十九届五中全会精神宣讲团,
基本事件总数n==15,
选中的4人恰好都是女生包含的基本事件个数m==6,
则选中的2人恰好都是女生的概率为P===2.2.
6.
【答案】
A
【考点】
空间向量
向量的线性运算性质及几何意义
【解析】
利用空间向量加法定理直接求解.
【解答】
在正方体ABCD−A1B1C1D1中,
∵ 点F是侧面CDD1C1的中心,∴ 连接DC1,D1C,交于点F,
=
=
=(-)
=+(-)
=-,
∵ =x+y+z,∴ x+y+z=1+=1.
7.
【答案】
A
【考点】
与直线关于点、直线对称的直线方程
【解析】
根据光学性质可知点A(2, 3)关于直线x+y+1=0的对称点 A′(−4, −3)在反射光线所在直线上,再根据两点式可得反射线所在直线方程.
【解答】
根据光学性质可知点A(2, 3)关于直线x+y+8=0的对称点 A′(−4,
由两点式可得反射光线所在直线方程为:=,化简得:2x−5y+1=3.
8.
【答案】
A
【考点】
双曲线的离心率
【解析】
结合双曲线的定义与正弦面积公式可推出sin∠F1PF2=,再由余弦定理可得cs∠F1PF2=1−,而,从而有=2,故得解.
【解答】
由双曲线的定义知,|PF1|−|PF2|=2a,
∵ |PF1|+|PF2|=6a,
∴ |PF1|=4a,|PF2|=2a,
∵ =|PF1|⋅|PF2|sin∠F1PF2,
∴ •4a⋅2a⋅sin∠F1PF2=,即sin∠F1PF2=,
在△PF1F2中,由余弦定理知,cs∠F1PF2===1−,
∵ ,
∴ ()2+(1−)2=1,
化简得,=2,
∴ 双曲线C的渐近线方程为y=±x=±x,即x±y=0.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.
【答案】
A,C
【考点】
空间向量的夹角与距离求解公式
【解析】
利用向量夹角公式直接求解.
【解答】
解:∵ a→=(−1,λ,−2),b→=(2,−1,1),a→与b→的夹角为120∘,
∴ cs
=a→⋅b→|a→|⋅|b→|
=−2−λ−25+λ2⋅6,
化简得:λ2−16λ−17=0,
解得λ=−1或λ=17.
故选AC.
【答案】
B,C
【考点】
空间向量的基本定理及其意义
空间向量的正交分解及其坐标表示
【解析】
利用向量的模的性质将的模转化为数量积求解,即可判断选项A,利用不共面的向量作为基底判断选项B,利用两个向量夹角的余弦公式进行求解,即可判断选项C,利用向量的夹角公式求出向量与的夹角,即可判断选项D.
【解答】
对于选项B,因为空间向量都是单位向量,且两两垂直,
所以不共面,而向量均与共面,
所以与不共面,
则可以构成空间的一个基底,
故选项B正确(1)对于选项C,设与的夹角为α,
则=,
所以向量和夹角的余弦值为,
故选项C 正确(2)对于选项D,因为,
同理可得,
则,
所以向量与的夹角为120∘,
则向量与不共线,
故选项D错误.
故选:BC.
【答案】
C,D
【考点】
互斥事件与对立事件
随机事件
【解析】
利用对立事件、互斥事件、相互独立事件的性质直接求解.
【解答】
对于A,若A,则P(AB)=0;
对于B,若事件A,则P(A+B)=P(A)+P(B);
对于C,∵ 对立事件一定是互斥事件,
∴ 若A,B是对立事件,B是互斥事件;
对于D,∵ 事件A,B恰好有一个发生和A,
∴ 事件A,B至少有一个发生的概率不小于A,故D正确.
【答案】
A,B,C
【考点】
双曲线的离心率
【解析】
选项A,结合|F1F2|==2c,b2=c2−a2与e=>1,可得关于e的方程,解之即可;
选项B,设内切圆I与△PF1F2的三边分别相切于点M,N,T,根据圆的切线长定理与双曲线的定义,可推出|F1T|=c+a,|F2T|=c−a,即T(a, 0);
选项C,设圆I的半径为r,则有|PF1|=|PF2|+λ|F1F2|,再利用双曲线的定义,即可得解;
选项D,假设点P在第一象限,设其坐标为(m, n),表示出|PH|2,|HA1|和|HA2|,再判断选项中的等式是否成立即可.
【解答】
设内切圆I与△PF2F2的三边分别相切于点M,N,T,如图所示,
由圆的切线长定理知,|PM|=|PN|1M|=|F8T|,|F2N|=|F2T|,
由双曲线的定义知,7a=|PF1|−|PF2|=|PM|+|F7M|−(|PN|+|F2N|)=|F1T|−|F4T|,
而|F1T|+|F2T|=7c,
∴ |F1T|=c+a,|F2T|=c−a,
∴ T(a, 5),故选项B正确(1)设圆I的半径为r,
∵ (λ∈R),
∴ |PF1|⋅r=|PF2|⋅r+λ•|F1F2|⋅r,即|PF3|=|PF2|+λ|F1F2|,
∴ |PF1|−|PF2|=λ|F3F2|,即2a=λ⋅6c,
∴ λ====,即选项C正确(2)假设点P在第一象限,设其坐标为(m,则-=1,
∵ PH垂直x轴于点H,
∴ |PH|4=n2=(1−)b2,|HA7|=m+a,|HA2|=m−a,
∴ |HA1|⋅|HA7|=(m+a)(m−a)=m2−a2,
若|PH|8=|HA1|⋅|HA2|,则(5−8=m2−a2,化简得m5=a2,
此时点P与H重合,不符合题意.
故选:ABC.
三、填空题:本题共4小题,每小题5分,共20分.
【答案】
−2
【考点】
直线的一般式方程与直线的垂直关系
【解析】
利用两条直线垂直的充要条件,列出关于m的方程,求解即可.
【解答】
因为直线l1:(m−1)x−3y+3=0和直线l2:2x+my−5=0垂直,
所以(m−1)×2+(−3)×m=0,解得m=−2.
【答案】
0.972
【考点】
相互独立事件的概率乘法公式
相互独立事件
互斥事件的概率加法公式
【解析】
利用n个独立重复试验中事件A恰好有k个发生的概率计算公式直接求解.
【解答】
现有3个灯泡并联而成的闭合电路,在某段时间内每个灯泡能正常照明的概率都是0.6,
∴ 在这段时间内该电路上的灯泡至少有两个能正常照明的概率是:
P==0.972.
【答案】
2
【考点】
平面的法向量
向量的数量积判断向量的共线与垂直
【解析】
由线面垂直得 // ,利用向量平行的性质能求出a+b的值.
【解答】
∵ 是直线l的方向向量,
是平面α的法向量,l⊥α,
∴ // ,
∴ ==,
解得a+b=2.
【答案】
8
【考点】
抛物线的性质
【解析】
利用抛物线的方程求出焦点坐标和准线方程,从而得到点M的坐标,设A(x1, y1),求出的表达式,然后利用基本不等式求解最值,从而得到最值成立的条件为y1=2,得到点A的坐标,从而求出AB的长度.
【解答】
抛物线的标准方程为x2=8y,
所以焦点F(4, 2),
因为抛物线的准线与y轴交于点M,
所以点M(0, −2),
设A(x1, y1),y8>0,则有,
所以,
,
所以=
=,
当且仅当,即y1=2时取等号,
所以当y3=2时,最大,2),
故AB=8+4=8.
答案为:5.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
【答案】
由已知可得,,,,
假设A、B、C三点共线,则存在实数λ,使得,
即(0, 1, −2)=λ(−2, 4, −3),则,此方程组无解,故不共线,
∴ A,B,C不共线,即过点A,B,C的平面是惟一的,
若点A,B,C,M共面,则存在x,y∈R,使得,
即(0, 3, −3)=x(0, 1, −2)+y(−2, 4, −3),
即,此方程组无解,
即不存在实数x,y,使得,即A、B、C、M不共面;
设平面α的法向量为,
则,取c=2,得.
∴ 点M到平面α的距离为d==.
【考点】
空间中的点的坐标
点、线、面间的距离计算
【解析】
(1)利用平面向量基本定理证明A,B,C共面,再由空间向量基本定理说明点A,B,C,M不共面即可;
(2)求出平面α的一个法向量,再求出的坐标,代入向量求点到面的距离公式求解.
【解答】
由已知可得,,,,
假设A、B、C三点共线,则存在实数λ,使得,
即(0, 1, −2)=λ(−2, 4, −3),则,此方程组无解,故不共线,
∴ A,B,C不共线,即过点A,B,C的平面是惟一的,
若点A,B,C,M共面,则存在x,y∈R,使得,
即(0, 3, −3)=x(0, 1, −2)+y(−2, 4, −3),
即,此方程组无解,
即不存在实数x,y,使得,即A、B、C、M不共面;
设平面α的法向量为,
则,取c=2,得.
∴ 点M到平面α的距离为d==.
【答案】
联立方程组7x−y−18=0y=x,解得x=3y=3,即C(3, 3).
设B(s, t),则边AB上的中点坐标为(s−12, t+52),
可得方程组s−12=t+527s−t−18=0,
解得s=2t=−4,即点B(2, −4);
设△ABC的外接圆方程为(x−a)2+(y−b)2=r2(r>0),
将三角形的三个顶点坐标代入,得:
(−1−a)2+(5−b)2=r2(2−a)2+(−4−b)2=r2(3−a)2+(3−b)2=r2.
解得a=−1b=0c=5.
所以三角形外接圆的方程为(x+1)2+y=25.
所以该圆的圆心坐标是(−1, 0),半径r=5.
圆心(−1, 0)到直线l2的方程为x−y=0的距离为:d=|−1−0|2=22.
所以弦长等于225−12=72.
【考点】
直线与圆的位置关系
【解析】
(1)联立方程组求得点C的坐标;设B(s, t),根据中点坐标公式求得线段AB中点坐标为(s−12, t+52),联立方程组求解.
(2)利用待定系数法确定⊙M的标准方程,求得圆心和半径,然后利用勾股定理、垂径定理和点到直线的距离公式解答.
【解答】
联立方程组7x−y−18=0y=x,解得x=3y=3,即C(3, 3).
设B(s, t),则边AB上的中点坐标为(s−12, t+52),
可得方程组s−12=t+527s−t−18=0,
解得s=2t=−4,即点B(2, −4);
设△ABC的外接圆方程为(x−a)2+(y−b)2=r2(r>0),
将三角形的三个顶点坐标代入,得:
(−1−a)2+(5−b)2=r2(2−a)2+(−4−b)2=r2(3−a)2+(3−b)2=r2.
解得a=−1b=0c=5.
所以三角形外接圆的方程为(x+1)2+y=25.
所以该圆的圆心坐标是(−1, 0),半径r=5.
圆心(−1, 0)到直线l2的方程为x−y=0的距离为:d=|−1−0|2=22.
所以弦长等于225−12=72.
【答案】
(1)解:从中任取一球,分别记得到黑球、黄球、绿球为事件A,B,C,
由于A,B,C为互斥事件,
根据已知得P(A)+P(B)+P(C)=1P(A)+P(B)=59P(B)+P(C)=23,
解得 P(A)=13P(A)+P(B)=29P(B)+P(C)=49
∴ 从中任取一球,得到黑球、黄球、绿球的概率分别是13,29,49.
(2)由(1)知黑球、黄球、绿球个数分别为3,2,4,
得到的两个球同色的可能有:两个黑球共3种情况,两个黄球只有1种情况,两个绿球共有6种情况,
而从9个球中取出2个球的情况共有36种,
所以所求概率为3+1+636=518,
则得到的两个球颜色不相同的概率是1−518=1318.
【考点】
互斥事件的概率加法公式
相互独立事件的概率乘法公式
【解析】
(1)从中任取一球,分别记得到黑球、黄球、绿球为事件A,B,C,由于A,B,C为互斥事件,列出方程组,由此能求出从中任取一球,得到黑球、黄球、绿球的概率.
(2)黑球、黄球、绿球个数分别为3,2,4,得到的两个球同色的可能有:两个黑球共3种情况,两个黄球只有1种情况,两个绿球共有6种情况,而从9个球中取出2个球的情况共有36种,由此能求出得到的两个球颜色不相同的概率.
【解答】
(1)解:从中任取一球,分别记得到黑球、黄球、绿球为事件A,B,C,
由于A,B,C为互斥事件,
根据已知得P(A)+P(B)+P(C)=1P(A)+P(B)=59P(B)+P(C)=23,
解得 P(A)=13P(A)+P(B)=29P(B)+P(C)=49
∴ 从中任取一球,得到黑球、黄球、绿球的概率分别是13,29,49.
(2)由(1)知黑球、黄球、绿球个数分别为3,2,4,
得到的两个球同色的可能有:两个黑球共3种情况,两个黄球只有1种情况,两个绿球共有6种情况,
而从9个球中取出2个球的情况共有36种,
所以所求概率为3+1+636=518,
则得到的两个球颜色不相同的概率是1−518=1318.
【答案】
动点P(x, y)到x轴的距离为y,到点M的距离为PM=,
因为动点P(x, y)(y>0)到定点M(0, 1)的距离比到x轴的距离大1,
所以=y+1,
两边平方可得,x2=4y,
故动点P的轨迹C的方程为x2=4y;
根据题意,显然直线l的斜率存在,
设直线l的斜率为k,则直线l的方程为y=kx+1,
设A(x1, y1),B(x2, y2),
由,消去x可得y2−(2+4k2)y+1=0,
所以,
所以AB=,解得k=±1,
所以直线l的方程为y=x+1或y=−x+1.
【考点】
轨迹方程
【解析】
(1)利用动点P(x, y)(y>0)到定点M(0, 1)的距离比到x轴的距离大1,直接利用坐标表示出等式,化简即可得到答案;
(2)设出直线l的方程,与抛物线的方程联立,然后利用焦点弦公式列出关于k的方程,求解即可得到答案.
【解答】
动点P(x, y)到x轴的距离为y,到点M的距离为PM=,
因为动点P(x, y)(y>0)到定点M(0, 1)的距离比到x轴的距离大1,
所以=y+1,
两边平方可得,x2=4y,
故动点P的轨迹C的方程为x2=4y;
根据题意,显然直线l的斜率存在,
设直线l的斜率为k,则直线l的方程为y=kx+1,
设A(x1, y1),B(x2, y2),
由,消去x可得y2−(2+4k2)y+1=0,
所以,
所以AB=,解得k=±1,
所以直线l的方程为y=x+1或y=−x+1.
【答案】
以D为坐标原点,分别以棱DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系如图所示,
则A(2, 0, 0),B(2, 2, 0),C(0, 2, 0),A1(2, 0, 2),B1(2, 2, 2),C1(0, 2, 2),D1(0, 0, 2),
因为E,F分别为BC,CD的中点,
所以点E(1, 2, 0),F(0, 1, 0)
所以,
设平面C1EF的法向量为,
则有,所以,
令z=1,则x=2,y=−2,所以,
又,
设平面AB1D1的法向量为,
则有,所以,
令c=1,则a=1,b=−1,所以,
设平面C1EF和平面AB1D1的夹角为θ,
所以=,
所以平面C1EF与平面AB1D1夹角的余弦值为;
因为,设点M的坐标为(x, y, z),
所以(x, y−2, z)=λ(2, −2, 0),
故点M的坐标为(2λ, 2−2λ, 0),
所以,
由(1)可知,平面C1EF的法向量为,
因为平面C1EF // 平面MB1D1,所以,
所以,解得.
【考点】
平面与平面平行的性质
二面角的平面角及求法
平面与平面平行的判定
【解析】
(1)以D为坐标原点,分别以棱DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系,求出各点的坐标,然利用待定系数法求出两个平面的法向量,利用二面角的计算公式,求出平面C1EF与平面AB1D1夹角的余弦值;
(2)设M点的坐标,利用,求出点M的坐标,然后将平面C1EF // 平面MB1D1,转化为平面C1EF的法向量垂直于平面MB1D1的向量,列出关于λ的方程,求解即可得到λ的值.
【解答】
以D为坐标原点,分别以棱DA,DC,DD1所在直线为x轴,y轴,z轴建立空间直角坐标系如图所示,
则A(2, 0, 0),B(2, 2, 0),C(0, 2, 0),A1(2, 0, 2),B1(2, 2, 2),C1(0, 2, 2),D1(0, 0, 2),
因为E,F分别为BC,CD的中点,
所以点E(1, 2, 0),F(0, 1, 0)
所以,
设平面C1EF的法向量为,
则有,所以,
令z=1,则x=2,y=−2,所以,
又,
设平面AB1D1的法向量为,
则有,所以,
令c=1,则a=1,b=−1,所以,
设平面C1EF和平面AB1D1的夹角为θ,
所以=,
所以平面C1EF与平面AB1D1夹角的余弦值为;
因为,设点M的坐标为(x, y, z),
所以(x, y−2, z)=λ(2, −2, 0),
故点M的坐标为(2λ, 2−2λ, 0),
所以,
由(1)可知,平面C1EF的法向量为,
因为平面C1EF // 平面MB1D1,所以,
所以,解得.
【答案】
由于P3,P4两点关于y轴对称,所以椭圆C必经过P3,P4两点,
又+>+,所以椭圆C不经过点P1,所以点P2在椭圆C上,
所以,解得,
所以椭圆C的方程为.
证明:因为点M在y轴上,且M为AB的中点,
所以直线AB平行于x轴,
设C(x1, y1),D(x2, y2),E(x3, y3),F(x4, y4),
设直线CD的方程为y=k1x+,代入椭圆C的方程中,得(+)x2+k1x−=0,
所以x1+x2=,x1x2=,
同理,设直线EF的方程为y=k2x+,则x3+x4=,x3x4=,
因为C、P、F三点共线,
所以==,解得xP=,
同理,由E、Q、D三点共线,可得xQ=,
所以xP+xQ=+
=
=
=
=
=
=0.
即xP=−xQ,
所以|xP|=|xQ|,即MP=MQ
【考点】
直线与椭圆的位置关系
椭圆的应用
【解析】
(1)由P3,P4关于y轴对称,知C必经过P3,P4,由+>+,知C过点P2,不过点P1,然后将P2和P4代入C的方程中,得到关于a和b的方程组,解之即可;
(2)设C(x1, y1),D(x2, y2),E(x3, y3),F(x4, y4),设直线CD的方程为y=k1x+,将其与椭圆方程联立,再结合韦达定理,表示出x1+x2和x1x2,同理可得x3+x4和x3x4,然后利用C、P、F三点共线,得xP,由E、Q、D三点共线,得xQ,最后证明xP+xQ=0,即可.
【解答】
由于P3,P4两点关于y轴对称,所以椭圆C必经过P3,P4两点,
又+>+,所以椭圆C不经过点P1,所以点P2在椭圆C上,
所以,解得,
所以椭圆C的方程为.
证明:因为点M在y轴上,且M为AB的中点,
所以直线AB平行于x轴,
设C(x1, y1),D(x2, y2),E(x3, y3),F(x4, y4),
设直线CD的方程为y=k1x+,代入椭圆C的方程中,得(+)x2+k1x−=0,
所以x1+x2=,x1x2=,
同理,设直线EF的方程为y=k2x+,则x3+x4=,x3x4=,
因为C、P、F三点共线,
所以==,解得xP=,
同理,由E、Q、D三点共线,可得xQ=,
所以xP+xQ=+
=
=
=
=
=
=0.
即xP=−xQ,
所以|xP|=|xQ|,即MP=MQ
2020-2021学年山东省济宁市高二(上)期末数学试卷人教A版: 这是一份2020-2021学年山东省济宁市高二(上)期末数学试卷人教A版,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年山东省高二(上)期中数学试卷人教A版: 这是一份2020-2021学年山东省高二(上)期中数学试卷人教A版,共10页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年山东省高二(上)期中数学试卷人教A版: 这是一份2020-2021学年山东省高二(上)期中数学试卷人教A版,共11页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












