四川省雅安市2020-2021学年九年级上学期期末数学试卷（word版含答案）

这是一份四川省雅安市2020-2021学年九年级上学期期末数学试卷（word版含答案），共23页。试卷主要包含了解答题解答应写出文字说明等内容，欢迎下载使用。
1．有一实物如图，那么它的主视图是（ ）
A．B．C．D．
2．下列关于x的方程中一定是一元二次方程的是（ ）
A．ax2+bx+c＝0B．x2﹣x（x+7）＝0
C．2x2﹣﹣1＝0D．x2﹣2x﹣3＝0
3．下列关系式中，表示y是x的反比例函数的是（ ）
A．y＝B．y＝C．y＝+1D．y＝
4．如图，在菱形ABCD中，对角线AC，BD相交于点O，AC＝8，BD＝6，点E，F分别为AO，DO的中点，则线段EF的长为（ ）
A．2.5B．3C．4D．5
5．在一个不透明的盒子里装有若干个白球和15个红球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过多次重复试验，发现摸到红球的频率稳定在0.6左右，则袋中白球约有（ ）
A．5个B．10个C．15个D．25个
6．将一元二次方程x2﹣8x﹣5＝0化成（x+a）2＝b（a，b为常数）形式，则a+b值为（ ）
A．25B．17C．29D．21
7．下列说法正确的是（ ）
A．矩形对角线相互垂直平分
B．对角线相等的菱形是正方形
C．两邻边相等的四边形是菱形
D．对角线分别平分对角的四边形是矩形
8．已知四条线段的长如下，则能成比例线段的是（ ）
A．1，1，2，3B．1，2，3，4C．1，2，2，4D．2，3，4，5
9．设a，b是方程x2+x﹣2021＝0的两个实数根，则（a﹣1）（b﹣1）的值为（ ）
A．2020B．﹣2021C．﹣2019D．2022
10．如图，下列条件中不能判定△ACD∽△ABC的是（ ）
A．∠ADC＝∠ACBB．C．∠ACD＝∠BD．AC2＝AD•AB
11．如图，在以O为原点的平面直角坐标系中，矩形OABC的两边OC，OA分别在x轴，y轴的正半轴上，反比例函数y＝（k≠0）的图象与AB相交于点D（2，6），与BC相交于点E，若BD＝3AD，则E点坐标为（ ）
A．（12，1）B．（4，3）C．（8，2）D．（8，）
12．如图，在平行四边形ABCD中，对角线AC的垂直平分线分别与AD，AC，BC相交于点E，O，F．下列结论正确的个数有（ ）
①四边形AFCE为菱形；
②△ABF≌△CDE；
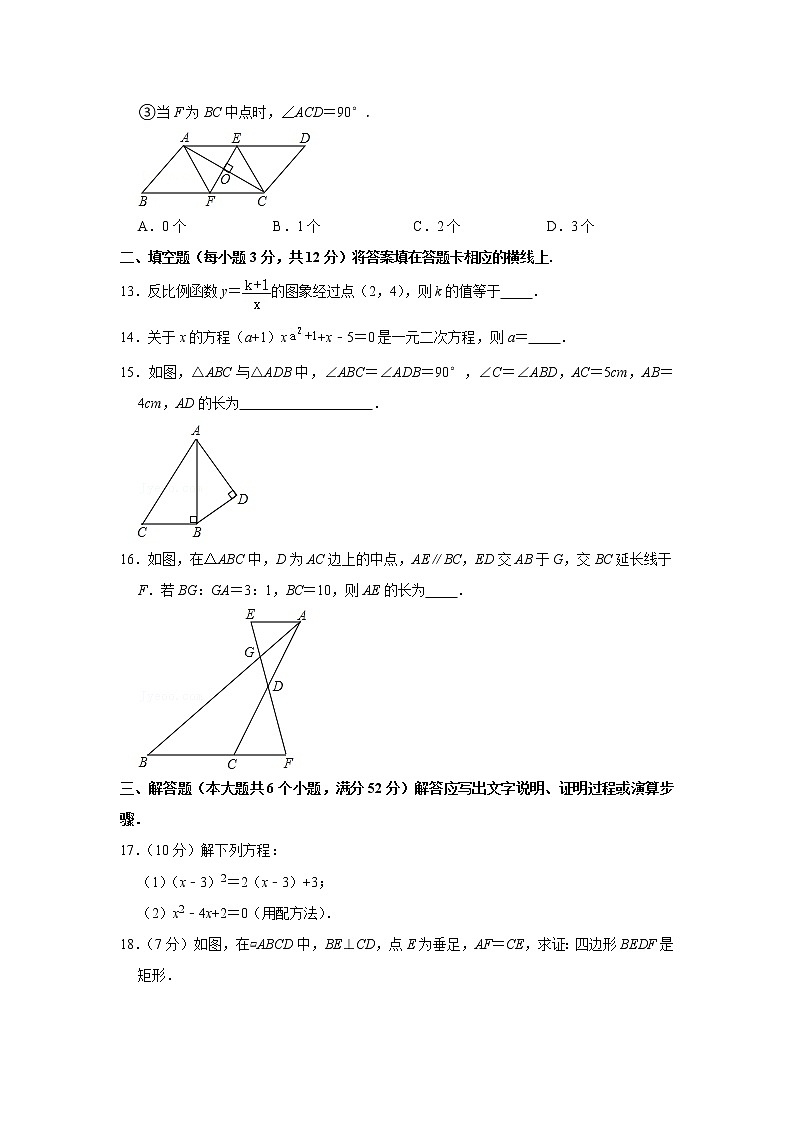
③当F为BC中点时，∠ACD＝90°．
A．0个B．1个C．2个D．3个
二、填空题（每小题3分，共12分）将答案填在答题卡相应的横线上.
13．反比例函数y＝的图象经过点（2，4），则k的值等于 ．
14．关于x的方程（a+1）x+x﹣5＝0是一元二次方程，则a＝ ．
15．如图，△ABC与△ADB中，∠ABC＝∠ADB＝90°，∠C＝∠ABD，AC＝5cm，AB＝4cm，AD的长为 ．
16．如图，在△ABC中，D为AC边上的中点，AE∥BC，ED交AB于G，交BC延长线于F．若BG：GA＝3：1，BC＝10，则AE的长为 ．
三、解答题（本大题共6个小题，满分52分）解答应写出文字说明、证明过程或演算步骤．
17．（10分）解下列方程：
（1）（x﹣3）2＝2（x﹣3）+3；
（2）x2﹣4x+2＝0（用配方法）．
18．（7分）如图，在▱ABCD中，BE⊥CD，点E为垂足，AF＝CE，求证：四边形BEDF是矩形．
19．（8分）某班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．
男、女生所选项目人数统计表
根据图表信息解决下列问题：
（1）m＝ ，n＝ ；
（2）求扇形统计图中机器人项目所对应扇形的圆心角度数；
（3）从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用画树状图或列表求所选取的2名学生中恰好有1名男生、1名女生的概率．
20．（8分）《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前．其中有首歌谣：今有竿不知其长，量得影长一丈五尺．立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺．同时立一根一尺五寸的小标杆，它的影长五寸（提示：1丈＝10尺，1尺＝10寸），问竹竿长为几丈几尺．
21．（9分）商场以每件200元的价格购进一批商品，以单价300元销售．预计每月可售出250件，该商场为尽可能减少库存，决定降价销售，根据市场调查，该商品单价每降低5元，可多售出25件，但最低售价应高于购进的价格；若该商场希望该商品每月获利28000元，则销售单价应定为多少元？每月可销售多少件？
22．（10分）如图，一次函数y1＝ax+b的图象与反比例函数y2＝的图象交于A，B两点，已知点A坐标（3，1），点B的坐标为（﹣，m）．
（1）求反比例函数的解析式和一次函数的解析式；
（2）观察图象，直接写出使函数值y1＜y2成立的自变量x的取值范围；
（3）求△OAB的面积．
四、填空题（每小题4分，共8分）将答案填在答题卡相应的横线上.
23．（4分）设x1、x2是方程x2﹣4x+1＝0的两个根，则x13+4x22+x1﹣1的值为 ．
24．（4分）将矩形纸片ABCD按如图所示的方式折叠，点B、D重合于对角线AC上的点O处．若AB＝6，则四边形AECF的面积为 ．
五、解答题（12分）解答应写出文字说明、证明过程或演算步骤．
25．（12分）如图，正方形ABCD中，点F是BC边上一点，连接AF，以AF为对角线作正方形AEFG，边FG与正方形ABCD的对角线AC相交于点H，连接DG．求证：
①∠EAB＝∠GAD；
②△AFC∽△AGD；
③DG⊥AC．
2020-2021学年四川省雅安市九年级（上）期末数学试卷
参考答案与试题解析
一、选择题（每题3分，共36分）下列各题的四个选项中，只有一个答案是正确的，请将正确答案的代号填涂在机读卡上.
1．有一实物如图，那么它的主视图是（ ）
A．B．C．D．
【分析】判断从几何体正面看得到的平面图形即可．
【解答】解：从正面看，得到的图形为，
故选：A．
2．下列关于x的方程中一定是一元二次方程的是（ ）
A．ax2+bx+c＝0B．x2﹣x（x+7）＝0
C．2x2﹣﹣1＝0D．x2﹣2x﹣3＝0
【分析】利用一元二次方程定义进行解答即可．
【解答】解：A、当a＝0时，不是一元二次方程，故此选项不合题意；
B、由已知方程得到：﹣7x＝0，属于一元一次方程，故此选项不合题意；
C、是分式方程，不是整式方程，故此选项不合题意；
D、是一元二次方程，故此选项符合题意．
故选：D．
3．下列关系式中，表示y是x的反比例函数的是（ ）
A．y＝B．y＝C．y＝+1D．y＝
【分析】利用反比例函数定义进行解答即可．
【解答】解：A、不是反比例函数，故此选项不合题意；
B、是正比例函数，不是反比例函数，故此选项不合题意；
C、不是反比例函数，故此选项不符合题意；
D、是反比例函数，故此选项符合题意；
故选：D．
4．如图，在菱形ABCD中，对角线AC，BD相交于点O，AC＝8，BD＝6，点E，F分别为AO，DO的中点，则线段EF的长为（ ）
A．2.5B．3C．4D．5
【分析】先依据菱形的性质求得OA、OD的长，然后依据勾股定理可求得AD的长，最后依据三角形中位线定理求的EF的长即可．
【解答】解：∵四边形ABCD为菱形，
∴AC⊥BD，OA＝OC＝AC＝4，OB＝OD＝BD＝3．
在Rt△AOD中，依据勾股定理可知：AD＝＝＝5．
∵点E，F分别为AO，DO的中点，
∴EF是△AOD的中位线，
∴EF＝AD＝2.5；
故选：A．
5．在一个不透明的盒子里装有若干个白球和15个红球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过多次重复试验，发现摸到红球的频率稳定在0.6左右，则袋中白球约有（ ）
A．5个B．10个C．15个D．25个
【分析】根据概率的求法，找准两点：①全部情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．
【解答】解：设袋中白球有x个，根据题意得：
＝0.6，
解得：x＝10，
经检验：x＝10是分式方程的解，
答：袋中白球约有10个．
故选：B．
6．将一元二次方程x2﹣8x﹣5＝0化成（x+a）2＝b（a，b为常数）形式，则a+b值为（ ）
A．25B．17C．29D．21
【分析】方程整理后判断即可求出a与b的值．
【解答】解：方程x2﹣8x﹣5＝0，
变形得：x2﹣8x＝5，
配方得：x2﹣8x+16＝21，即（x﹣4）2＝21，
则a＝﹣4，b＝21，
故a+b＝﹣4+21＝17，
故选：B．
7．下列说法正确的是（ ）
A．矩形对角线相互垂直平分
B．对角线相等的菱形是正方形
C．两邻边相等的四边形是菱形
D．对角线分别平分对角的四边形是矩形
【分析】根据矩形的性质可得A错误；先判定四边形是菱形，再判定是矩形就是正方形可得B正确；根据菱形的判定可得C错误；根据对角线的关系判定矩形，从而得D错误．
【解答】解：A．矩形的对角线相等且平分，故A原说法错误，不符合题意；
B．对角线相等的菱形是正方形，正确，符合题意；
C．四条边相等的四边形是菱形，故C原说法错误，不符合题意；
D．对角线互相平分且相等的四边形是矩形，故D原说法错误，不符合题意；
故选：B．
8．已知四条线段的长如下，则能成比例线段的是（ ）
A．1，1，2，3B．1，2，3，4C．1，2，2，4D．2，3，4，5
【分析】根据成比例线段的定义逐项判定即可得到结论．
【解答】解：A、∵1×2≠1×3，
∴1，1，2，3不能成比例线段，故不符合题意；
B、∵1×4≠2×3，
∴1，2，3，4不能成比例线段，故不符合题意；
C、∵1:2＝2:4，
∴1，2，2，4；能成比例线段，故符合题意；
D、∵2×5≠3×4，
∴2，3，4，5不能成比例线段，故不符合题意；
故选：C．
9．设a，b是方程x2+x﹣2021＝0的两个实数根，则（a﹣1）（b﹣1）的值为（ ）
A．2020B．﹣2021C．﹣2019D．2022
【分析】由根与系数的关系可求得a+b与ab的值，代入求值即可．
【解答】解：∵a，b是方程x2+x﹣2021＝0的两个实数根，
∴a+b＝﹣1，ab＝﹣2021，
∴（a﹣1）（b﹣1）＝ab﹣a﹣b+1＝ab﹣（a+b）+1＝﹣2021﹣（﹣1）+1＝﹣2019，
故选：C．
10．如图，下列条件中不能判定△ACD∽△ABC的是（ ）
A．∠ADC＝∠ACBB．C．∠ACD＝∠BD．AC2＝AD•AB
【分析】根据相似三角形的判定逐一判断可得．
【解答】解：A、由∠ADC＝∠ACB，∠A＝∠A可得△ACD∽△ABC，此选项不符合题意；
B、由不能判定△ACD∽△ABC，此选项符合题意；
C、由∠ACD＝∠B，∠A＝∠A可得△ACD∽△ABC，此选项不符合题意；
D、由AC2＝AD•AB，即＝，且∠A＝∠A可得△ACD∽△ABC，此选项不符合题意；
故选：B．
11．如图，在以O为原点的平面直角坐标系中，矩形OABC的两边OC，OA分别在x轴，y轴的正半轴上，反比例函数y＝（k≠0）的图象与AB相交于点D（2，6），与BC相交于点E，若BD＝3AD，则E点坐标为（ ）
A．（12，1）B．（4，3）C．（8，2）D．（8，）
【分析】根据待定系数法求得反比例函数的解析式，由题意可知E的横坐标为8，代入解析式即可求得纵坐标．
【解答】解：∵四边形OCBA是矩形，
∴AB＝OC，OA＝BC，
∵D（2，6），
∴AD＝2，OA＝6，
∵BD＝3AD，
∴AB＝8，
∵反比例函数y＝（k≠0）的图象与AB相交于点D（2，6），
∴k＝2×6＝12，
∴y＝，
把x＝8代入得，y＝，
∴E的坐标为（8，），
故选：D．
12．如图，在平行四边形ABCD中，对角线AC的垂直平分线分别与AD，AC，BC相交于点E，O，F．下列结论正确的个数有（ ）
①四边形AFCE为菱形；
②△ABF≌△CDE；
③当F为BC中点时，∠ACD＝90°．
A．0个B．1个C．2个D．3个
【分析】由平行四边形的性质、全等三角形的判定与性质、菱形的判定与性质分别对各个结论进行判断即可．
【解答】解：∵四边形ABCD为平行四边形，
∴AD∥BC，AD＝BC，AB＝CD，∠B＝∠D，AB∥CD，
∴∠EAC＝∠FCA，
∵EF垂直平分AC，
∴OA＝OC，EA＝EC，
∴∠EAC＝∠ECA，
∴∠FCA＝∠ECA，
在△AOE和△COF中，
，
∴△AOE≌△COF（ASA），
∴OE＝OF，
∴四边形AFCE为平行四边形，
∵EF垂直平分AC，
∴平行四边形AFCE是菱形，①正确；
∴AE＝CF，
∴BF＝DE，
在△ABF和△CDE中，
，
∴△ABF≌△CDE（SAS），②正确；
∵四边形AFCE是菱形，
∴AF＝CF，
∵F为BC的中点，
∴BF＝CF，
∴AF＝CF＝BC，
∴∠BAC＝90°，
∵AB∥CD，
∴∠ACD＝∠BAC＝90°，③正确；
正确的个数有3个，
故选：D．
二、填空题（每小题3分，共12分）将答案填在答题卡相应的横线上.
13．反比例函数y＝的图象经过点（2，4），则k的值等于 7 ．
【分析】将点的坐标代入反比例函数解析式即可解答．
【解答】解：将点（2，4）代入y＝得，
k+1＝xy＝2×4＝8．
∴k＝7，
故答案为：7．
14．关于x的方程（a+1）x+x﹣5＝0是一元二次方程，则a＝ 1 ．
【分析】根据一元二次方程的定义，令二次项次数为2，二次项系数不等于0，解答即可．
【解答】解：∵方程（a+1）x+x﹣5＝0是一元二次方程，
∴a²+1＝2且a+1≠0，
∴a＝±1且a≠﹣1，
∴a＝1，
故答案是：1．
15．如图，△ABC与△ADB中，∠ABC＝∠ADB＝90°，∠C＝∠ABD，AC＝5cm，AB＝4cm，AD的长为 ．
【分析】根据相似三角形的判定与性质即可求出答案．
【解答】解：∵∠ABC＝∠ADB＝90°，∠C＝∠ABD，
∴△ACB∽△ABD，
∴，
∴AD＝＝cm，
故答案为：
16．如图，在△ABC中，D为AC边上的中点，AE∥BC，ED交AB于G，交BC延长线于F．若BG：GA＝3：1，BC＝10，则AE的长为 5 ．
【分析】先根据平行线分线段成比例求出BF：AE的值，再根据D是AC的中点得到CF与AE相等，列出等式求解即可．
【解答】解：∵AE∥BC
∴△AEG∽△BFG
∴BG：GA＝3：1＝BF：AE
∵D为AC边上的中点
∴AE：CF＝1：1
∴AE＝CF
∴BF：AE＝（CF+BC）：AE＝3：1
∴（AE+10）：AE＝3：1
解得：AE＝5．
三、解答题（本大题共6个小题，满分52分）解答应写出文字说明、证明过程或演算步骤．
17．（10分）解下列方程：
（1）（x﹣3）2＝2（x﹣3）+3；
（2）x2﹣4x+2＝0（用配方法）．
【分析】（1）利用因式分解法求解即可；
（2）利用配方法求解即可．
【解答】解：（1）∵（x﹣3）2＝2（x﹣3）+3，
∴（x﹣3）2﹣2（x﹣3）﹣3＝0，
∴（x﹣3﹣3）（x﹣3+1）＝0，
∴x1＝6，x2＝2；
（2）∵x2﹣4x+4﹣2＝0，
∴（x﹣2）2＝2，
则x﹣2＝，
∴x1＝2+，x2＝2﹣．
18．（7分）如图，在▱ABCD中，BE⊥CD，点E为垂足，AF＝CE，求证：四边形BEDF是矩形．
【分析】由平行四边形的性质得到AB∥CD，AB＝CD，推出四边形BEDF是平行四边形，证出∠BED＝90°，根据矩形的判定定理即可得到结论．
【解答】证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝CD，
∵AF＝CE，
∴FB＝ED．
∴四边形BEDF是平行四边形，
∵BE⊥CD，
∴∠BED＝90°．
∴四边形BEDF是矩形．
19．（8分）某班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．
男、女生所选项目人数统计表
根据图表信息解决下列问题：
（1）m＝ 8 ，n＝ 3 ；
（2）求扇形统计图中机器人项目所对应扇形的圆心角度数；
（3）从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用画树状图或列表求所选取的2名学生中恰好有1名男生、1名女生的概率．
【分析】（1）用航模的人数除以它所占的百分比得到调查的总人数为40，然后计算m、n的值；
（2）用机器人项目所占的百分比乘以360°即可；
（3）将选航模项目的2名男生编上号码1，2，将2名女生编上号码3，4． 画树状图展示所有12种可能出现的结果，找出“1名男生、1名女生”的结果数，然后根据概率公式计算．
【解答】解：（1）∵调查的总人数为4÷10%＝40（人），
∴m＝40%×30﹣4＝8；
n＝40﹣16﹣12﹣4﹣5＝3；
故答案8，3；
（2）扇形统计图中机器人项目所对应扇形的圆心角度数为360°×＝144°；
（3）将选航模项目的2名男生编上号码1，2，将2名女生编上号码3，4．
画树状图为：
共有12种可能出现的结果，并且它们都是等可能的，其中“1名男生、1名女生”有8种可能，
所以 P（1名男生、1名女生）＝＝．
20．（8分）《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前．其中有首歌谣：今有竿不知其长，量得影长一丈五尺．立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五尺．同时立一根一尺五寸的小标杆，它的影长五寸（提示：1丈＝10尺，1尺＝10寸），问竹竿长为几丈几尺．
【分析】根据同一时刻物高与影长成正比可得出结论．
【解答】解：设竹竿的长度为x尺，
∵竹竿的影长＝一丈五尺＝15尺，标杆长＝一尺五寸＝1.5尺，影长五寸＝0.5尺，
∴＝，
解得x＝45（尺）．
答：竹竿长为4丈5尺．
21．（9分）商场以每件200元的价格购进一批商品，以单价300元销售．预计每月可售出250件，该商场为尽可能减少库存，决定降价销售，根据市场调查，该商品单价每降低5元，可多售出25件，但最低售价应高于购进的价格；若该商场希望该商品每月获利28000元，则销售单价应定为多少元？每月可销售多少件？
【分析】设售价降低x个5元，由销售额﹣进价＝利润，作为相等关系列方程，解方程求解后要代入实际问题中检验是否符合题意，进行值的取舍．
【解答】解：设售价降低x个5元，得
（300﹣200﹣5x）（250+25x）＝28000．
解得：x1＝4，x2＝6．
当x＝4时，300﹣5×4＝280（元）＞200元；
当x＝6时，300﹣5×6＝270（元）＞200元；
因为要减少库存，
所以，售价为：300﹣5×6＝270（元）．
销售件数为：250+6×25＝400（件）．
答：售价应定为270元，每月销售400件．
22．（10分）如图，一次函数y1＝ax+b的图象与反比例函数y2＝的图象交于A，B两点，已知点A坐标（3，1），点B的坐标为（﹣，m）．
（1）求反比例函数的解析式和一次函数的解析式；
（2）观察图象，直接写出使函数值y1＜y2成立的自变量x的取值范围；
（3）求△OAB的面积．
【分析】（1）将点A的坐标代入可确定反比例函数关系式，进而确定点B的坐标，再利用待定系数法求出一次函数关系式；
（2）根据图象直接得出答案；
（3）求出直线AB与y轴交点D的坐标，确定OD的长，再根据三角形的面积公式进行计算即可．
【解答】解：（1）将A（3，1）代入反比例函数y2＝得，
k＝3×1＝3，
∴反比例函数解析式为y2＝；
把点B（﹣，m）代入反比例函数关系式得，
m＝﹣2，
∴点B（﹣，﹣2），
把A（3，1），B（﹣，﹣2）代入一次函数y1＝ax+b得，
，
解得a＝，b＝﹣1，
∴一次函数的关系式为y1＝x﹣1，
答：一次函数的关系式为y1＝x﹣1，反比例函数解析式为y2＝；
（2）由图象知，当x＜﹣或0＜x＜3时，y1＜y2；
（3）一次函数y1＝x﹣1与y轴的交点D（0，﹣1），
∴OD＝1，
∴S△AOB＝S△AOD+S△BOD
＝×1×3+×1×
＝．
四、填空题（每小题4分，共8分）将答案填在答题卡相应的横线上.
23．（4分）设x1、x2是方程x2﹣4x+1＝0的两个根，则x13+4x22+x1﹣1的值为 55 ．
【分析】根据根与系数的关系即可求出答案．
【解答】解：由题意可知：x1+x2＝4，x1x2＝1，
＝4x1﹣1，
∴＝4﹣x1，
∴原式＝4﹣x1+4+x1﹣1
＝4（+）﹣1
＝4（x1+x2）2﹣8x1x2﹣1
＝4×16﹣8﹣1
＝55，
故答案为：55
24．（4分）将矩形纸片ABCD按如图所示的方式折叠，点B、D重合于对角线AC上的点O处．若AB＝6，则四边形AECF的面积为 8 ．
【分析】根据折叠得到AD＝AC，进而得到∠DCA角度，在Rt△ACD和Rt△ADF中，利用勾股定理求AD和DF的长求解．
【解答】解：∵四边形ABCD是矩形，
∴AB＝CD，AD＝BC，∠D＝90°，
∵矩形纸片ABCD按如图所示的方式折叠，点B、D重合于对角线AC上的点O处，
∴AO＝AD＝CB＝CO＝，
在Rt△ACD中，AD＝，
∴∠ACD＝30°，∠DAC＝60°，
由折叠可知，∠DAF＝∠CAD＝30°，
设AD＝x，则AC＝2x，
在Rt△ACD中，AB＝CD＝6，
根据勾股定理得：AC2﹣AD2＝CD2，
∴4x2﹣x2＝36，
解得x＝2，
在Rt△ADF中，同理可得DF＝2，
∴CF＝CD﹣CF＝4，
∴S四边形AECF＝CF•AD＝4×＝8，
故答案为8．
五、解答题（12分）解答应写出文字说明、证明过程或演算步骤．
25．（12分）如图，正方形ABCD中，点F是BC边上一点，连接AF，以AF为对角线作正方形AEFG，边FG与正方形ABCD的对角线AC相交于点H，连接DG．求证：
①∠EAB＝∠GAD；
②△AFC∽△AGD；
③DG⊥AC．
【分析】①由正方形的性质可得∠EAG＝∠BAD＝90°，∠FAG＝∠AFG＝∠DAC＝∠ACB＝45°，AF＝AG，AC＝AD，可得∠EAB＝∠GAD；②由＝＝，∠FAC＝∠DAG，可证△AFC∽△AGD；③由相似三角形的性质可得∠ADG＝∠ACB＝45°，可得∠AND＝90°，可证DG⊥AC．
【解答】证明：①∵四边形ABCD，四边形AEFG为正方形，
∴∠EAG＝∠BAD＝90°，
∠FAG＝∠AFG＝∠DAC＝∠ACB＝45°，AF＝AG，AC＝AD，
∴∠EAG﹣∠BAG＝∠BAD﹣∠BAG，
∴∠EAB＝∠GAD；
②∵AF＝AG，AC＝AD，
∴＝＝，
∵∠FAG＝∠CAD＝45°，
∴∠FAC＝∠DAG，
∴△AFC∽△AGD；
③由②可得，
∴∠ADG＝∠ACB＝45°，
延长DG交AC于N，
∵∠CAD＝45°，∠ADG＝45°，
∴∠AND＝90°，
∴DG⊥AC．
项目
男生（人数）
女生（人数）
机器人
7
9
3D打印
m
4
航模
2
2
其他
5
n
项目
男生（人数）
女生（人数）
机器人
7
9
3D打印
m
4
航模
2
2
其他
5
n