辽宁省盘锦市兴隆台区2020-2021学年九年级上学期期末数学试卷（word版含答案）

这是一份辽宁省盘锦市兴隆台区2020-2021学年九年级上学期期末数学试卷（word版含答案），共31页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年辽宁省盘锦市兴隆台区九年级（上）期末数学试卷
一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中只有一项是符合题目要求的）
1．下列图形中，是中心对称图形的是（　　）
A．正三角形 B．平行四边形 C．正五边形 D．直角三角形
2．下列说法正确的是（　　）
A．中奖概率为0.001，只要抽1000次，就肯定能中奖
B．概率很小的事件不可能发生
C．投一枚图钉，可以用列举法求得“针尖朝上”的概率
D．“任意画一个多边形，其外角和都是360°”为必然事件
3．如图，点A、B、C、D在⊙O上，∠BDC＝30°，点B是的中点，则∠AOC＝（　　）

A．36° B．72° C．120° D．60°
4．下列方程中没有实数根的是（　　）
A．x2+x+2＝0 B．2x＝0 C．x2﹣2+2＝0 D．2x2﹣7x＝1
5．下列关于三角形外心的说法中，正确的是（　　）
A．三角形的外心是三角形各角平分线的交点
B．三角形的外心是三角形三边中线的交点
C．三角形的外心是三角形三边高线的交点
D．三角形的外心是三角形三边垂直平分线的交点
6．若x＝2是一元二次方程kx2+3x+2＝0的一个解，则k的值是（　　）
A．﹣2 B．2 C．0 D．﹣2或0
7．如图，AB，BC和AC分别为⊙O内接正方形，正六边形和正n边形的一边，则n是（　　）

A．六 B．八 C．十 D．十二
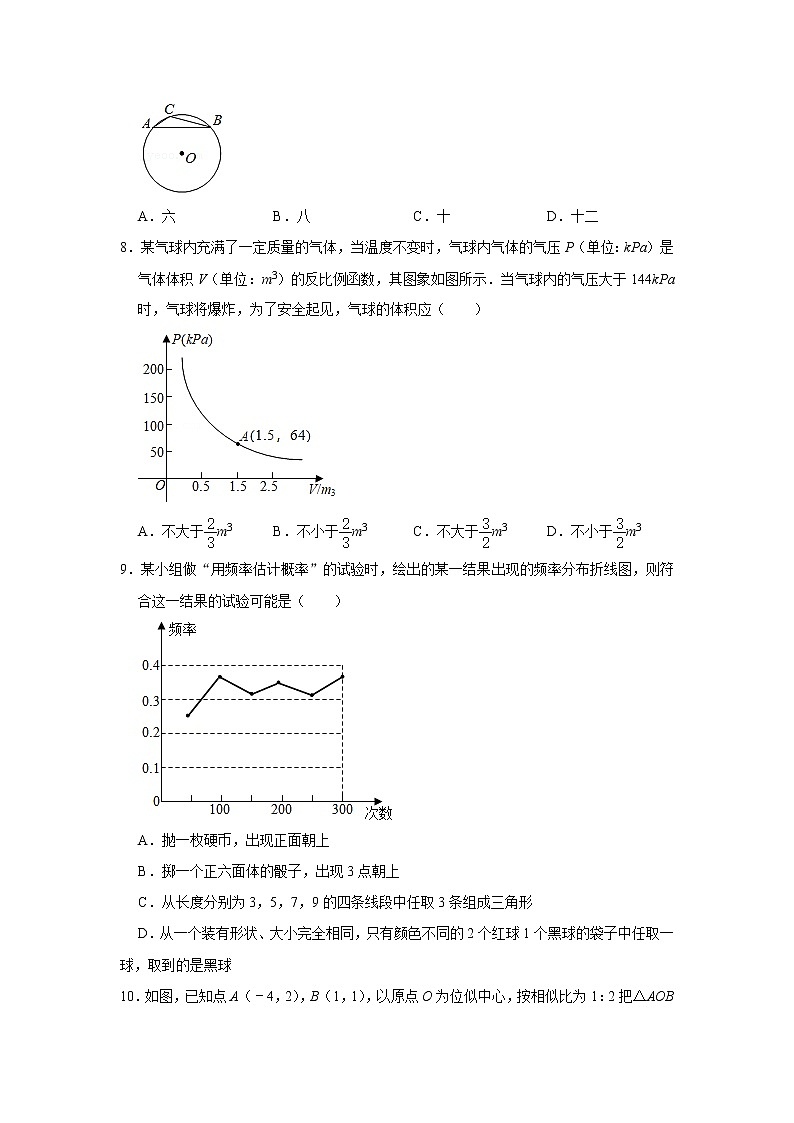
8．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（单位：kPa）是气体体积V（单位：m3）的反比例函数，其图象如图所示．当气球内的气压大于144kPa时，气球将爆炸，为了安全起见，气球的体积应（　　）

A．不大于m3 B．不小于m3 C．不大于m3 D．不小于m3
9．某小组做“用频率估计概率”的试验时，绘出的某一结果出现的频率分布折线图，则符合这一结果的试验可能是（　　）

A．抛一枚硬币，出现正面朝上
B．掷一个正六面体的骰子，出现3点朝上
C．从长度分别为3，5，7，9的四条线段中任取3条组成三角形
D．从一个装有形状、大小完全相同，只有颜色不同的2个红球1个黑球的袋子中任取一球，取到的是黑球
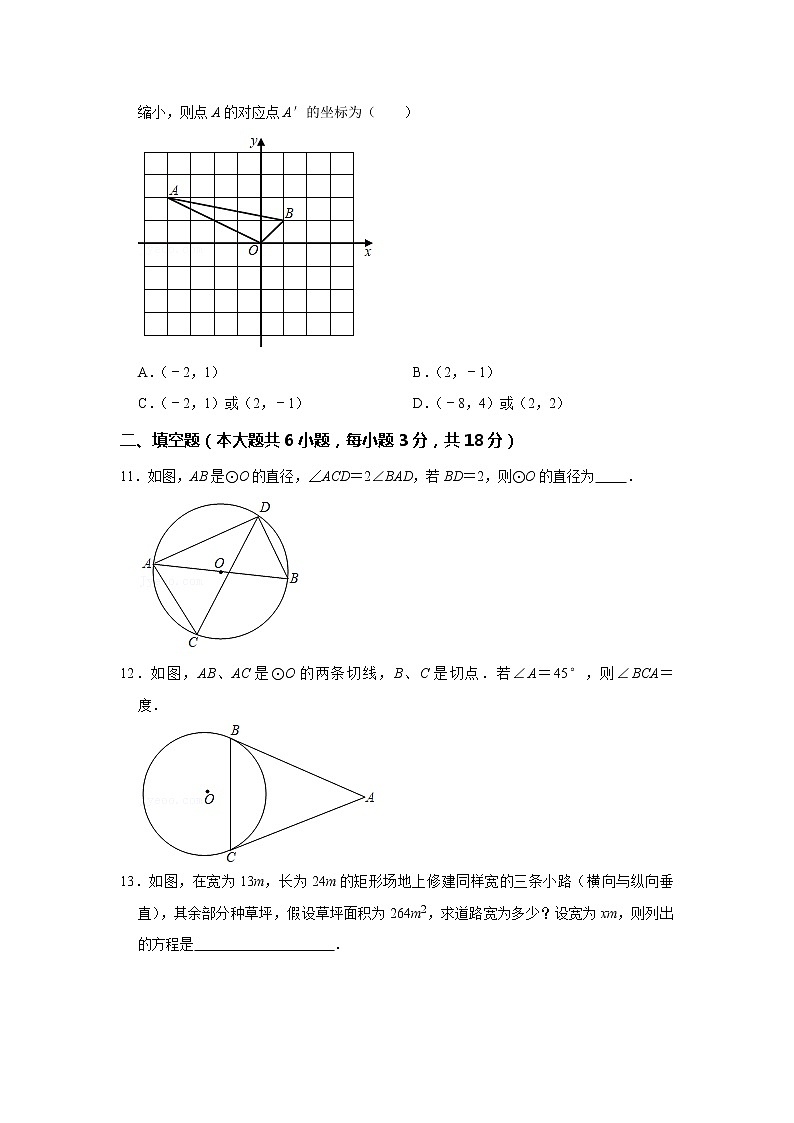
10．如图，已知点A（﹣4，2），B（1，1），以原点O为位似中心，按相似比为1：2把△AOB缩小，则点A的对应点A′的坐标为（　　）

A．（﹣2，1） B．（2，﹣1）
C．（﹣2，1）或（2，﹣1） D．（﹣8，4）或（2，2）
二、填空题（本大题共6小题，每小题3分，共18分）
11．如图，AB是⊙O的直径，∠ACD＝2∠BAD，若BD＝2，则⊙O的直径为　 　．

12．如图，AB、AC是⊙O的两条切线，B、C是切点．若∠A＝45°，则∠BCA＝　 　度．

13．如图，在宽为13m，长为24m的矩形场地上修建同样宽的三条小路（横向与纵向垂直），其余部分种草坪，假设草坪面积为264m2，求道路宽为多少？设宽为xm，则列出的方程是　 　．

14．如图，Rt△AOB中，∠ABO＝90°，反比例函数y＝（k≠0）的图象与AB交于点C，且AC：CB＝3：1，若S△AOB＝8，则k的值为　 　．

15．抛物线y＝ax2+a﹣2与x轴有两个交点，且当x＞0时，y随x的增大而增大，则a的取值范围是　 　．
16．如图，在△ABC中，AB＝6，BC＝8，AC＝7，点D，E分别在AB，BC上，将△BDE沿ED折叠，点B的对应点F刚好落在AC上．当△CEF与△ABC相似时，BE的长为　 　．

三、解答题（本大题共3小题，每小题10分，共30分，解答应写出必要的文字说明、证明过程或演算步骤）
17．解下列方程：
（1）2x2+3x﹣4＝0；
（2）5x（2x+1）＝6x+3．
18小英和小亮两人玩儿摸球游戏．把标号分别为1，2，3，4的大小形状完全相同的小球装在一个不透明的口袋中．小英随机摸取一个小球然后放回，小亮再随机摸出一个小球．
（1）下面的游戏规则中，你认为对双方公平的是哪几个？（写出序号即可）
①两人摸出的小球的标号之和是奇数时，小英获胜；否则小亮获胜；
②两人摸出的小球的标号的乘积能被2整除时，小英获胜；否则小亮获胜；
③两人摸出的小球的标号的乘积能被3整除时，小英获胜；否则小亮获胜；
④两人摸出的小球的标号的乘积能被4整除时，小英获胜；否则小亮获胜；
（2）如果你是小英，为了获胜，你想选择上面（1）中的哪一种规则？并说明理由．
19阅读下列材料：
小金遇到了这样的一个问题：如图1，O是等边三角形ABC内一点，OA＝3，OB＝4，OC＝5，求∠AOB的度数．
小金的思路是：如图2，构造△ABO′，使△AO′B≌△COB，再用勾股定理的逆定理和等边三角形的性质，求出∠AOB的度数．
解：将线段BO绕点B逆时针旋转60°，得到线段BO′，连接O′A，OO′．
∴BO＝BO′，∠OBO′＝…
（1）请你按小金的思路将本题的解答过程补充完整；
（2）“如图3，点P为正方形ABCD内的一点，PA＝1，PB＝2，PC＝3，求∠APB的度数”．请你根据（1）的解题思路完成：
①给出辅助线作法，并画出对应的图形（不必写出解答过程）；
②直接写出∠APB的度数．

四、解答题（本大题共2小题，每小题10分，共20分，解答应写出必要的文字说明、证明过程或演算步骤）
20已知抛物线y＝﹣2x2+4x+6．
（1）请用配方法将y＝﹣2x2+4x+6化为y＝a（x﹣h）2+k的形式，并写出对称轴和顶点的坐标；
（2）在平面直角坐标系中，画出y＝﹣2x2+4x+6的图象；
（3）如果该抛物线沿x轴向左或向右平移m（m＞0）个单位后经过原点，求m的值；
（4）当0≤x≤4时，求y的取值范围．

21如图，在平面直角坐标系中，一次函数y＝kx（k≠0）与反比例函数y＝（m≠0）的图象交于点A和点B，已知点A的坐标为（3，1）．
（1）求反比例函数表达式；
（2）若点P为y轴上一动点，当△ABP的面积为4时，求点P的坐标；
（3）根据图象直接写出当kx＞时，x的取值范围．

五、解答题（本大题共2小题，共24分，每小题12分，解答应写出必要的文字说明、证明过程或演算步骤）
22如图，AB是⊙O的弦，半径OC⊥AB于点D，点E在射线OC上，且∠OEB＝∠OAB．
（1）求证：BE是⊙O的切线；
（2）若AB＝2，∠OAB＝30°，求图中阴影部分弓形的面积．

23某超市以每个15元的批发价购进一批花盆．按每个25元出售，平均每天可以卖出60个．经过市场调查发现，单价每降价1元，平均每天就要多卖出10个．
（1）若超市采用降价销售的方式，当定价多少时，平均每天获利630元？
（2）若降价后超市每天的其他费用为100元，定价是多少时，超市利润最大？最大利润是多少？
六、解答题（本大题共1题，共14分，解答应写出必要的文字说明、证明过程或演算步骤）
24（1）巩固基础
如图，在△ABC中，点D，E分别在AB，AC上，且DE∥BC，过点A作射线分别交DE于F，于BC与G，求证：
＝．
（2）迁移应用
如图2，在Rt△ACB中，∠C＝90°，BC＝3，AB＝5，点D为AC边上一点，点E在BD上，且EF∥AC，EG∥BC，若EF：EG＝1：3，求CD的长．

七、解答题（本大题共1题，共14分，解答应写出必要的文字说明、证明过程或演算步骤）
25如图，抛物线y＝ax2+bx+3经过点A（﹣1，0），B（3，0），与y轴交于点C．
（1）求该抛物线的解析式；
（2）若点D是抛物线的顶点，判断△BCD的形状，并说明理由；
（3）抛物线上是否存在一点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．


参考答案与试题解析
一．选择题（共10小题）
1．下列图形中，是中心对称图形的是（　　）
A．正三角形 B．平行四边形 C．正五边形 D．直角三角形
【分析】根据中心对称图形的概念求解．
【解答】解：A、正三角形是轴对称图形，不是中心对称图形，故此选项不合题意；
B、平行四边形是中心对称图形，故此选项正确；
C、正五边形是轴对称图形，不是中心对称图形，故此选项不合题意；
D、直角三角形不是中心对称图形，故此选项不合题意；
故选：B．
2．下列说法正确的是（　　）
A．中奖概率为0.001，只要抽1000次，就肯定能中奖
B．概率很小的事件不可能发生
C．投一枚图钉，可以用列举法求得“针尖朝上”的概率
D．“任意画一个多边形，其外角和都是360°”为必然事件
【分析】本题考查的是必然事件、不可能事件、随机事件的概念，掌握其概念是解决此题关键．
【解答】解：A、买彩票中奖的概率为0.001，并不意味着买1000张彩票就一定能中奖，只有当买彩票的数量非常大时，才可以看成中奖的频率接近中奖的概率0.001，故说法错误；
B、概率很小的事件也有可能发生，故说法错误；
C、投一枚图钉，“针尖朝上”，无法利用列举法求概率，故说法错误；
D、“任意画一个多边形，其外角和都是360°”为必然事件，说法正确．
故选：D．
3．如图，点A、B、C、D在⊙O上，∠BDC＝30°，点B是的中点，则∠AOC＝（　　）

A．36° B．72° C．120° D．60°
【分析】如图，连接OB，由圆周角定理推知∠BOC＝60°，然后根据圆心角、弧的关系求得答案．
【解答】解：如图，连接OB，
∵＝，∠BDC＝30°，
∴∠BOC＝2∠BDC＝60°．
又∵点B是的中点，
∴＝．
∴∠AOB＝∠BOC＝60°．
∴∠AOC＝∠AOB+∠BOC＝120°．
故选：C．

4．下列方程中没有实数根的是（　　）
A．x2+x+2＝0 B．2x＝0 C．x2﹣2+2＝0 D．2x2﹣7x＝1
【分析】分别计算出各选项中方程的判别式或方程的根，从而做出判断．
【解答】解：A．方程x2+x+2＝0中Δ＝12﹣4×1×2＝﹣7＜0，没有实数根，符合题意；
B．方程2x＝0的根为x＝0，不符合题意；
C．方程x2﹣2+2＝0中Δ＝（﹣2）2﹣4×1×2＝0，有两个相等的实数根，不符合题意；
D．方程2x2﹣7x＝1，即2x2﹣7x﹣1＝0中Δ＝（﹣7）2﹣4×2×（﹣1）＝57＞0，有两个不相等的实数根，不符合题意．
故选：A．
5．下列关于三角形外心的说法中，正确的是（　　）
A．三角形的外心是三角形各角平分线的交点
B．三角形的外心是三角形三边中线的交点
C．三角形的外心是三角形三边高线的交点
D．三角形的外心是三角形三边垂直平分线的交点
【分析】利用三角形的外心的性质分别判断得出即可．
【解答】解：∵三角形的外心是三角形三边垂直平分线的交点，
∴A、B、C选项错误，D选项正确，
故选：D．
6．若x＝2是一元二次方程kx2+3x+2＝0的一个解，则k的值是（　　）
A．﹣2 B．2 C．0 D．﹣2或0
【分析】把x＝2代入方程kx2+3x+2＝0得：4k+6+2＝0，然后通过解方程确定k的值．
【解答】解：把x＝2代入方程kx2+3x+2＝0得：4k+6+2＝0，
解得k＝﹣2．
∵方程kx2+3x+2＝0是关于x的一元二次方程，
∴k≠0．
故选：A．
7．如图，AB，BC和AC分别为⊙O内接正方形，正六边形和正n边形的一边，则n是（　　）

A．六 B．八 C．十 D．十二
【分析】根据正多边形中心角的定义求出，∠AOB，∠BOC可得结论．
【解答】解：连接OA，OB，OC．

由题意，∠AOB＝＝90°，∠BOC＝＝60°，
∴∠AOC＝∠AOB﹣∠BOC＝30°，
∴n＝＝12，
故选：D．
8．某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（单位：kPa）是气体体积V（单位：m3）的反比例函数，其图象如图所示．当气球内的气压大于144kPa时，气球将爆炸，为了安全起见，气球的体积应（　　）

A．不大于m3 B．不小于m3 C．不大于m3 D．不小于m3
【分析】根据题意可知温度不变时，气球内气体的气压P（kPa）是气体体积V（m3）的反比例函数，且过点（1.5，64）故P•V＝96；故当P≤144，可判断V≥．
【解答】解：设球内气体的气压P（kPa）和气体体积V（m3）的关系式为P＝
∵图象过点（1.5，64）
∴k＝96，
即P＝在第一象限内，P随V的增大而减小，
∴当P≤144时，V≥＝．
故选：B．
9．某小组做“用频率估计概率”的试验时，绘出的某一结果出现的频率分布折线图，则符合这一结果的试验可能是（　　）

A．抛一枚硬币，出现正面朝上
B．掷一个正六面体的骰子，出现3点朝上
C．从长度分别为3，5，7，9的四条线段中任取3条组成三角形
D．从一个装有形状、大小完全相同，只有颜色不同的2个红球1个黑球的袋子中任取一球，取到的是黑球
【分析】利用折线统计图可得出试验的频率在0.33左右，进而得出答案．
【解答】解：A、抛一枚硬币，出现正面朝上的概率为0.5，不符合这一结果；
B、掷一个正六面体的骰子，出现3点朝上为，不符合这一结果；
C、从长度分别为3、5、7、9的4条线段中任取3条作三角形的边，等可能的结果有：3、5、7；3、7、9；5、7、9；3、7、9，
且能组成三角形的有：3、5、7；5、7、9；3、7、9；
∴能组成三角形的概率为，不符合这一结果；
D、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球的概率为，符合这一结果．
故选：D．
10．如图，已知点A（﹣4，2），B（1，1），以原点O为位似中心，按相似比为1：2把△AOB缩小，则点A的对应点A′的坐标为（　　）

A．（﹣2，1） B．（2，﹣1）
C．（﹣2，1）或（2，﹣1） D．（﹣8，4）或（2，2）
【分析】根据位似变换的性质计算，得到答案．
【解答】解：∵以原点O为位似中心，按相似比为1：2把△AOB缩小，点A的坐标为（﹣4，2），
∴点A的对应点A′的坐标为（﹣4×，2×）或（﹣4×（﹣），2×（﹣）），即（﹣2，1）或（2，﹣1），
故选：C．
二．填空题（共6小题）
11．如图，AB是⊙O的直径，∠ACD＝2∠BAD，若BD＝2，则⊙O的直径为　4　．

【分析】利用圆周角定理得到：∠ADB＝90°，∠ACD＝∠B，结合三角形内角和定理和已知条件可以判定∠DAB＝30°，则AB＝2BD，此题得解．
【解答】解：∵AB是⊙O的直径，
∴∠ADB＝90°．
∵＝．
∴∠ACD＝∠ABD．
又∵∠ACD＝2∠BAD，∠BAD+∠ABD＝90°，
∴∠BAD＝30°．
∵BD＝2，
∴AB＝2BD＝4．
故答案是：4．
12．如图，AB、AC是⊙O的两条切线，B、C是切点．若∠A＝45°，则∠BCA＝　67.5　度．

【分析】根据切线长定理可得AB＝AC，再由∠A的度数可得答案．
【解答】解：∵AB、AC是⊙O的两条切线，B、C是切点，
∴AB＝AC，
∴∠BCA＝∠CBA，
∵∠A＝45°，
∴∠BCA＝×（180°﹣45°）＝67.5°．
故答案为：67.5．
13．如图，在宽为13m，长为24m的矩形场地上修建同样宽的三条小路（横向与纵向垂直），其余部分种草坪，假设草坪面积为264m2，求道路宽为多少？设宽为xm，则列出的方程是　（13﹣x）（24﹣2x）＝264　．

【分析】设宽为xm，剩下的耕田面积可平移成长方形，且能表示出长和宽，从而根据面积可列出方程．
【解答】解：设宽为xm，（13﹣x）（24﹣2x）＝264．
故答案为：（13﹣x）（24﹣2x）＝264．
14．如图，Rt△AOB中，∠ABO＝90°，反比例函数y＝（k≠0）的图象与AB交于点C，且AC：CB＝3：1，若S△AOB＝8，则k的值为　4　．

【分析】设出OB和BC的长度，可以表示出C点坐标，由此得到k与参数的关系，利用△AOB的面积为8，得到所设参数的方程，进而求出k．
【解答】解：设OB＝m，BC＝n，
∴C（m，n），
∵C点在反比例函数的图象上，
∴k＝mn，
∵AC：CB＝3：1，
∴AC＝3CB＝3n，
∴AB＝AC+CB＝4n，
∵S△AOB＝8，
∴，
∴4mn＝16，
∴mn＝4，
∴k＝mn＝4，
故答案为：4．
15．抛物线y＝ax2+a﹣2与x轴有两个交点，且当x＞0时，y随x的增大而增大，则a的取值范围是　a＞0　．
【分析】由抛物线y＝ax2+a﹣2与x轴有两个交点，可得，Δ＝a2﹣4a×（﹣2）＞0，可求得a的范围a＞0或a＜﹣8；又当x＞0时，y随x的增大而增大，且抛物线的对称轴为直线：x＝﹣，可得，抛物线的开口向上，即a＞0，综合可得结论．
【解答】解：∵抛物线y＝ax2+a﹣2与x轴有两个交点，
∴Δ＝a2﹣4a×（﹣2）＝a2+8a＞0，
∴a＞0或a＜﹣8，
由抛物线y＝ax2+a﹣2可知，抛物线对称轴为直线：x＝﹣，
又当x＞0时，y随x的增大而增大，
∴抛物线开口向上，即a＞0，
综上，a的取值范围为a＞0．
故答案为：a＞0．
16．如图，在△ABC中，AB＝6，BC＝8，AC＝7，点D，E分别在AB，BC上，将△BDE沿ED折叠，点B的对应点F刚好落在AC上．当△CEF与△ABC相似时，BE的长为　或　．

【分析】根据折叠的性质得到BE＝EF，根据相似三角形的性质即可得到结论．
【解答】解：∵将△BDE沿DE翻折得到△FDE，
∴BE＝EF，
∵BC＝8，
∴CE＝8﹣BE，
当△CEF与△ABC相似时，＝或＝，即＝或＝，
解得：BE＝或，
故答案是：或．

三、解答题（本大题共3小题，每小题10分，共30分，解答应写出必要的文字说明、证明过程或演算步骤）
17．解下列方程：
（1）2x2+3x﹣4＝0；
（2）5x（2x+1）＝6x+3．
【分析】（1）先求出b2﹣4ac的值，再代入公式求出答案即可；
（2）整理后分解因式，即可得出两个一元一次方程，求出方程的解即可．
【解答】解：（1）2x2+3x﹣4＝0，
这里a＝2，b＝3，c＝﹣4，
∵Δ＝b2﹣4ac＝32﹣4×2×（﹣4）＝41，
∴x＝＝，
解得：x1＝，x2＝；

（2）5x（2x+1）＝6x+3，
∵整理得：10x2﹣x﹣3＝0，
∴（2x+1）（5x﹣3）＝0，
∴2x+1＝0或5x﹣3＝0，
解得：x1＝﹣，x2＝．
18小英和小亮两人玩儿摸球游戏．把标号分别为1，2，3，4的大小形状完全相同的小球装在一个不透明的口袋中．小英随机摸取一个小球然后放回，小亮再随机摸出一个小球．
（1）下面的游戏规则中，你认为对双方公平的是哪几个？（写出序号即可）
①两人摸出的小球的标号之和是奇数时，小英获胜；否则小亮获胜；
②两人摸出的小球的标号的乘积能被2整除时，小英获胜；否则小亮获胜；
③两人摸出的小球的标号的乘积能被3整除时，小英获胜；否则小亮获胜；
④两人摸出的小球的标号的乘积能被4整除时，小英获胜；否则小亮获胜；
（2）如果你是小英，为了获胜，你想选择上面（1）中的哪一种规则？并说明理由．
【考点】列表法与树状图法；游戏公平性．菁优网版权所有
【专题】概率及其应用；推理能力．
【答案】见试题解答内容
【分析】（1）根据题意列出图表得出所有等可能的情况数，找出符合条件的情况数，然后根据概率公式即可得出答案；
（2）根据（1）小英胡获胜的概率，找出概率最大的即可得出答案．
【解答】解：（1）列表如下：

1
2
3
4
1
（1，1）
（2，1）
（3，1）
（4，1）
2
（1，2）
（2，2）
（3，2）
（4，2）
3
（1，3）
（2，3）
（3，3）
（4，3）
4
（1，4）
（2，4）
（3，4）
（4，4）
所有等可能的情况有16种，
①两次摸出的球的标号之和为偶数和奇数的情况都是8种，
则P（小英获胜）＝，P（小亮获胜）＝，二者相等，说明游戏公平．
②两人摸出的小球的标号的乘积能被2整除的有12种，
则P（小英获胜）＝＝，P（小亮获胜）＝，二者不相等，说明游戏不公平．
③两人摸出的小球的标号的乘积能被3整除的有7种，
则P（小英获胜）＝，P（小亮获胜）＝，二者不相等，说明游戏不公平．
④两人摸出的小球的标号的乘积能被4整除的有8种，
则P（小英获胜）＝＝，P（小亮获胜）＝，二者相等，说明游戏公平．
游戏对双方公平的是①④；

（2）如果我是小英，为了获胜，我应选择②，这样获胜的概率比较大．
19阅读下列材料：
小金遇到了这样的一个问题：如图1，O是等边三角形ABC内一点，OA＝3，OB＝4，OC＝5，求∠AOB的度数．
小金的思路是：如图2，构造△ABO′，使△AO′B≌△COB，再用勾股定理的逆定理和等边三角形的性质，求出∠AOB的度数．
解：将线段BO绕点B逆时针旋转60°，得到线段BO′，连接O′A，OO′．
∴BO＝BO′，∠OBO′＝…
（1）请你按小金的思路将本题的解答过程补充完整；
（2）“如图3，点P为正方形ABCD内的一点，PA＝1，PB＝2，PC＝3，求∠APB的度数”．请你根据（1）的解题思路完成：
①给出辅助线作法，并画出对应的图形（不必写出解答过程）；
②直接写出∠APB的度数．

【考点】全等三角形的判定与性质；等边三角形的性质；勾股定理；勾股定理的逆定理；正方形的性质；作图﹣旋转变换．菁优网版权所有
【专题】作图题；推理能力；应用意识．
【答案】（1）150°．
（2）①作图见解析部分．
②135°
【分析】（1）由SAS可证△BO′A≌△BOC，可得OC＝O'A＝5，利用勾股定理的逆定理即可证得△AOO′是直角三角形，即可求解．
（2）①将△BCP绕点B顺时针旋转90°得到△BAE，然后连接PE，图形如图2所示．
②根据旋转的性质知△BCP≌△BAE．由全等三角形的对应边相等、等腰三角形的判定推知△BPE是等腰三角形，则∠BPE＝∠BEP＝45°；然后由全等三角形的对应边相等、勾股定理证得∠APE＝90°；最后根据图中角与角间的数量关系求得∠APB＝135°．
【解答】解：（1）如图1中，

∵将线段BO以点B为旋转中心逆时针旋转60°得到线段BO'，
∴∠OBO'＝60°，AO'＝CO＝5，
∵△BOB'是等边三角形，
∴∠BOO'＝60°，
∵AO2+OO2＝25＝O'A2，
∴∠AOO'＝90°，
∴∠AOB＝150°；

（2）①将△BCP绕点B顺时针旋转90°得到△BAE，然后连接PE，图形如图2所示．

②∵根据旋转的性质知∠PBE＝90°，△BCP≌△BAE．
∴BP＝BE，PC＝AE，
∴∠BPE＝∠BEP＝45°．
又PA＝1，PB＝2，PC＝3，PE＝PB＝2，
∴AE2＝AP2+PE2，
∴∠APE＝90°，
∴∠APB＝∠APE+∠BPE＝90°+45°＝135°，即图2中∠APB的度数为135°．
四、解答题（本大题共2小题，每小题10分，共20分，解答应写出必要的文字说明、证明过程或演算步骤）
20已知抛物线y＝﹣2x2+4x+6．
（1）请用配方法将y＝﹣2x2+4x+6化为y＝a（x﹣h）2+k的形式，并写出对称轴和顶点的坐标；
（2）在平面直角坐标系中，画出y＝﹣2x2+4x+6的图象；
（3）如果该抛物线沿x轴向左或向右平移m（m＞0）个单位后经过原点，求m的值；
（4）当0≤x≤4时，求y的取值范围．

【考点】二次函数的性质；二次函数图象上点的坐标特征；二次函数图象与几何变换；二次函数的三种形式．菁优网版权所有
【专题】二次函数图象及其性质；几何直观；运算能力．
【答案】（1）对称轴为：直线x＝1，顶点坐标为：（1，8）；
（2）见解答；
（3）m＝3或1；
（4）﹣10≤y≤8．
【分析】（1）直接利用配方法求出二次函数顶点坐标和对称轴得出答案；
（2）利用（1）中所求进而画出函数图象；
（3）直接利用函数图象得出即可；
（4）直接利用二次函数增减性以及结合极值法求出y的取值范围．
【解答】解：（1）由题意可得：y＝﹣2x2+4x+6＝﹣2（x﹣1）2+8，
对称轴为：直线x＝1，顶点坐标为：（1，8）；

（2）如图所示：

（3）由图象可知，抛物线沿x轴向左平移3个单位或向右平移1个单位后经过原点，
∴m＝3或1；

（4）当0≤x≤4时，
当x＝1，y＝8，当x＝4，y＝﹣10，
则y的取值范围为：﹣10≤y≤8．
21如图，在平面直角坐标系中，一次函数y＝kx（k≠0）与反比例函数y＝（m≠0）的图象交于点A和点B，已知点A的坐标为（3，1）．
（1）求反比例函数表达式；
（2）若点P为y轴上一动点，当△ABP的面积为4时，求点P的坐标；
（3）根据图象直接写出当kx＞时，x的取值范围．

【考点】反比例函数与一次函数的交点问题．菁优网版权所有
【专题】一次函数及其应用；反比例函数及其应用；几何直观；运算能力．
【答案】（1）反比例函数表达式为y＝；
（2）点P的坐标为（0，）或（0，﹣）；
（3）﹣3＜x＜0或x＞3．
【分析】（1）根据待定系数法即可求得；
（2）根据反比例函数和正比例函数的对称性求得B的坐标，然后根据三角形面积公式得到S△ABP＝OP•（3+3）＝4，求得OP的长，即可求得P的坐标；
（3）根据图象即可求得．
【解答】解：（1）∵反比例函数y＝（m≠0）的图象经过点A（3，1），
∴m＝3×1＝3，
∴反比例函数表达式为y＝；
（2）∵一次函数y＝kx（k≠0）与反比例函数y＝（m≠0）的图象交于点A和点B，点A的坐标为（3，1），
∴B（﹣3，﹣1），
∴S△ABP＝OP•（3+3）＝4，
∴OP＝，
∴点P的坐标为（0，）或（0，﹣）；
（3）观察图象，当kx＞时，x的取值范围是﹣3＜x＜0或x＞3．
五、解答题（本大题共2小题，共24分，每小题12分，解答应写出必要的文字说明、证明过程或演算步骤）
22如图，AB是⊙O的弦，半径OC⊥AB于点D，点E在射线OC上，且∠OEB＝∠OAB．
（1）求证：BE是⊙O的切线；
（2）若AB＝2，∠OAB＝30°，求图中阴影部分弓形的面积．

【考点】勾股定理；垂径定理；切线的判定与性质；扇形面积的计算．菁优网版权所有
【专题】证明题；与圆有关的位置关系；运算能力；推理能力．
【答案】（1）证明过程见解析；
（2）﹣．
【分析】（1）连接OB，由直角三角形的性质及等腰三角形的性质得出∠OBE＝90°，则可得出结论；
（2）由直角三角形的性质得出OD＝AD＝1，∠AOD＝60°，根据扇形的面积公式可得出答案．
【解答】（1）证明：连接OB，

∵OA＝OB，
∴∠OAB＝∠OBA，
∵OC⊥AB，
∴∠BDE＝90°，
∴∠DBE+∠OEB＝90°，
∵∠OEB＝∠OAB，
∴∠OBA+∠DBE＝90°，
∴∠OBE＝90°，
∴OB⊥BE，
∴BE是⊙O的切线；
（2）解：∵OD⊥AB，AB＝2，
∴AD＝AB＝，
∵∠OAB＝30°，
∴OD＝AD＝1，∠AOD＝60°，
∴OA＝2，∠AOB＝2∠AOD＝120°，
∴S△AOB＝AB×OD＝×1＝，S扇形AOB＝＝π，
∴阴影部分弓形的面积为S扇形AOB﹣S△AOB＝π﹣．
23某超市以每个15元的批发价购进一批花盆．按每个25元出售，平均每天可以卖出60个．经过市场调查发现，单价每降价1元，平均每天就要多卖出10个．
（1）若超市采用降价销售的方式，当定价多少时，平均每天获利630元？
（2）若降价后超市每天的其他费用为100元，定价是多少时，超市利润最大？最大利润是多少？
【考点】一元二次方程的应用；二次函数的应用．菁优网版权所有
【专题】二次函数的应用；应用意识．
【答案】（1）当定价为24元或22元时，平均每天获利630元；（2）定价是23元时，超市利润最大，最大利润是540元．
【分析】（1）设定价为x元，根据题意列出关于x的一元二次方程，求解即可；
（2）根据题意列出函数解析式，再根据函数的性质求函数最值即可．
【解答】解：（1）设定价是x元，由题意，得：
[（25﹣x）×10+60]×（x﹣15）＝630，
化简，得：﹣10x2+460x﹣4650＝630，
解得：x1＝24，x2＝22，
答：当定价为24元或22元时，平均每天获利630元；
（2）设获利为w元，
则w＝[（25﹣x）×10+60]×（x﹣15）﹣100＝﹣10x2+460x﹣4750＝﹣10（x﹣23）2+540，
∵﹣10＜0，抛物线开口向下，w有最大值，
∴当x＝23时，w有最大值，最大值为540元．
答：定价是23元时，超市利润最大，最大利润是540元．
六、解答题（本大题共1题，共14分，解答应写出必要的文字说明、证明过程或演算步骤）
24（1）巩固基础
如图，在△ABC中，点D，E分别在AB，AC上，且DE∥BC，过点A作射线分别交DE于F，于BC与G，求证：
＝．
（2）迁移应用
如图2，在Rt△ACB中，∠C＝90°，BC＝3，AB＝5，点D为AC边上一点，点E在BD上，且EF∥AC，EG∥BC，若EF：EG＝1：3，求CD的长．

【考点】相似形综合题．菁优网版权所有
【专题】几何综合题；图形的相似；推理能力．
【答案】（1）答案见解答过程；
（2）．
【分析】（1）证明△ADF∽△ABG，△AEF∽△ACG，根据相似三角形的性质得到＝，＝，等量代换证明结论；
（2）过点D作DH∥BC交AB于H，根据相似三角形的性质得到DH＝3CD，再证明△ADH∽△ACB，根据相似三角形的性质列出比例式，求出CD．
【解答】（1）证明：∵DE∥BC，
∴△ADF∽△ABG，△AEF∽△ACG，
∴＝，＝，
∴＝，
∴＝；
（2）解：过点D作DH∥BC交AB于H，
∵EG∥BC，
∴EG∥DH，
∴△BEG∽△BDH，
∴＝，
∵EF∥AC，
∴＝，
∴＝，
∴＝＝，即DH＝3CD，
在Rt△ACB中，∠C＝90°，BC＝3，AB＝5，
则AC＝＝＝4，
∵DH∥BC，
∴△ADH∽△ACB，
∴＝，即＝，
解得：CD＝．

七、解答题（本大题共1题，共14分，解答应写出必要的文字说明、证明过程或演算步骤）
25如图，抛物线y＝ax2+bx+3经过点A（﹣1，0），B（3，0），与y轴交于点C．
（1）求该抛物线的解析式；
（2）若点D是抛物线的顶点，判断△BCD的形状，并说明理由；
（3）抛物线上是否存在一点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．

【考点】二次函数综合题．菁优网版权所有
【专题】代数几何综合题；分类讨论；待定系数法；推理能力．
【答案】（1）y＝﹣x2+2x+3；
（2）△BCD是直角三角形，理由见解析；
（3）（，），（，﹣）．
【分析】（1）直接根据待定系数法求二次函数表达式即可；
（2）根据题意过点D作DE⊥x轴，垂足为点E，过点C作CF⊥DE，垂足为点F，由二次函数的顶点式得到D坐标为（1，4），从而根据各点的坐标推出，BC＝3，CD＝，BD＝2，进而得到BC2+CD2＝BD2，由勾股定理的逆定理可推出△BCD是直角三角形；
（3）假设抛物线上存在一点P（x，﹣x2+2x+3），使得△ACP是以AC为直角边的直角三角形，并分当点P当∠ACP＝90°时和当∠ACP＝90°时两种情况进行讨论，通过辅助线构造相似三角形Rt△AOC∽Rt△CMP，Rt△AOC∽Rt△PNA，利用其性质求解即可．
【解答】解：（1）根据题意将点A（﹣1，0），B（3，0）代入y＝ax2+bx+3，
得：，
解得，
∴抛物线的解析式为：y＝﹣x2+2x+3；
（2）如图1所示，

过点D作DE⊥x轴，垂足为点E，过点C作CF⊥DE，垂足为点F，
根据（1）中的结论，y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴抛物线的顶点D坐标为（1，4），
令x＝0，则y＝3，则点C（0，3），
∴OC＝3，OB＝3，BC＝＝3，
CF＝1，DF＝1，CD＝＝，
BE＝2，DE＝4，BD＝＝2，
∵，即BC2+CD2＝BD2，
∴△BCD是直角三角形；
（3）假设抛物线上存在一点P，使得△ACP是以AC为直角边的直角三角形，设点P（x，﹣x2+2x+3），
当∠ACP＝90°时，如图2所示，

过点P作PM⊥OC，垂足为点M，
∴CM＝3﹣（﹣x2+2x+3）＝x2﹣2x，PM＝x，
∵∠ACO+∠CAO＝90°，∠ACO+∠PCM＝90°，
∴∠CAO＝∠PCM，
∴Rt△AOC∽Rt△CMP，
∴＝，即＝，
解得x＝或x＝0（舍去），
当x＝时，y＝，
此时点P坐标为（，）；
当∠CAP＝90°时，如图3所示，

过点P作PN⊥x轴，垂足为点N，
∴PN＝﹣（﹣x2+2x+3）＝x2﹣2x﹣3，AN＝x+1，
∵∠ACO+∠CAO＝90°，∠CAO+∠PAN＝90°，
∴∠AOC＝∠PAN，
∴Rt△AOC∽Rt△PNA，
∴＝，即＝，
解得x＝或x＝﹣1（舍去），
当x＝时，y＝﹣，
此时点P坐标为（，﹣），
综上所述，点P坐标为（，），（，﹣）．