重庆市酉阳土家族苗族自治县2020-2021学年九年级上学期期末数学试题(word版含答案)

这是一份重庆市酉阳土家族苗族自治县2020-2021学年九年级上学期期末数学试题(word版含答案)，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
重庆市酉阳土家族苗族自治县2020-2021学年九年级上学期期末数学试题
学校:___________姓名：___________班级：___________考号：___________


一、单选题
1．在平面直角坐标系中，点关于原点对称的点的坐标是（ ）
A． B． C． D．
2．下列4个图形中，是中心对称图形但不是轴对称的图形是（　　）．
A． B． C． D．
3．方程的解是（ ）
A． B． C．， D．，
4．“射击运动员射击一次，命中靶心”这个事件是（ ）
A．确定事件 B．必然事件 C．不可能事件 D．随机事件
5．抛物线的对称轴是（ ）
A．轴 B．直线 C．直线 D．直线
6．在一个不透明的口袋中，装有个红球个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（ ）
A． B． C． D．
7．如图，是的直径，点C，D在上，若，则的度数为（　　　）

A．55° B．45° C．35° D．25°
8．如图⊙O的直径垂直于弦，垂足是，，，的长为（ ）

A． B．4 C． D．8
9．如图，将△ABC绕点C顺时针方向旋转40°得△A’CB’，若AC⊥A’B’，则∠BAC等于（ ）

A．50° B．60° C．70° D．80°
10．某药品原价每盒元，为响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒元，如果该药品平均每次降价的百分率是x，那么列方程正确的是（ ）
A． B． C． D．
11．下列图形是由小圆按一定的规律组成，其中图①中有个小圆，图②中一共有个小圆，图③中一共有个小圆，…，按此规律，第⑥个图形中共有小圆的个数为（ ）

A．81 B．76 C．70 D．51
12．在这六个数中，随机取出一个数记为，那么使得关于的一元二次方程有解，且使得关于的方程有整数解的所有的值之和为（　）
A． B． C． D．

二、填空题
13．抛物线的开口方向是______________．
14．冉超不会做最后一个选择题，在四个选项中随便选了一个，则他选对的概率是_______．
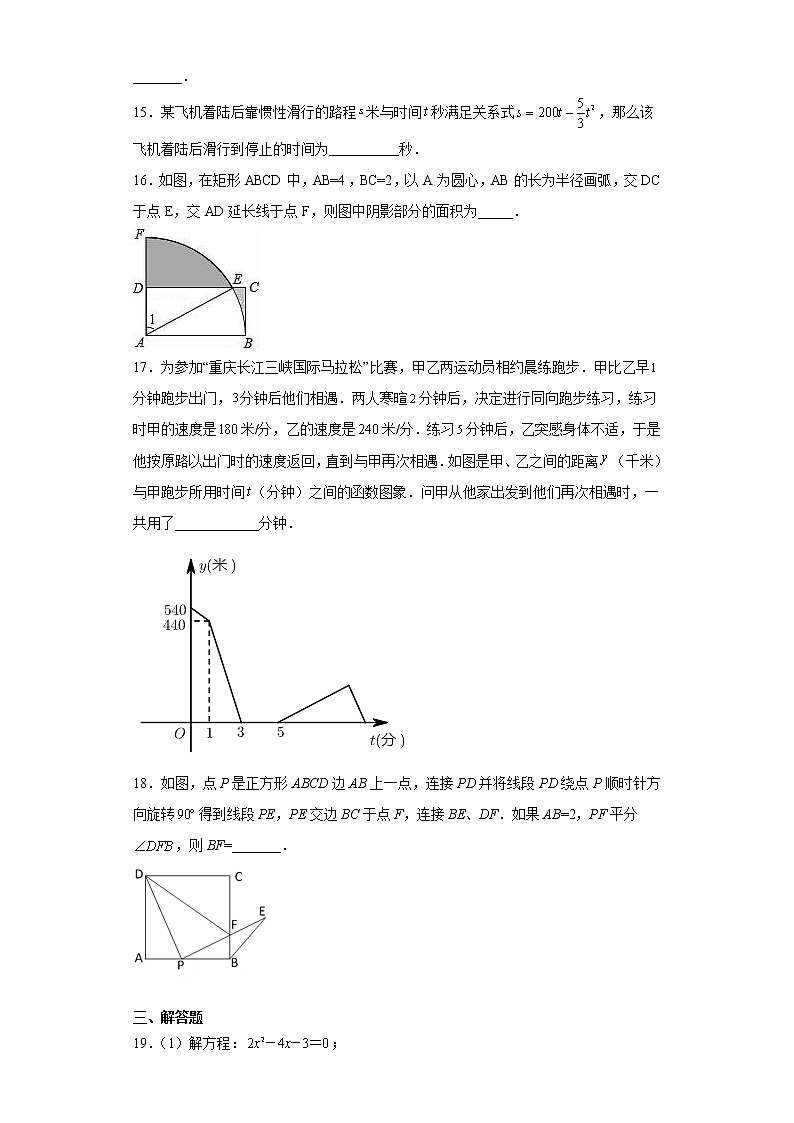
15．某飞机着陆后靠惯性滑行的路程米与时间秒满足关系式，那么该飞机着陆后滑行到停止的时间为__________秒．
16．如图，在矩形ABCD中，AB=4，BC=2，以A为圆心，AB的长为半径画弧，交DC于点E，交AD延长线于点F，则图中阴影部分的面积为_____．

17．为参加“重庆长江三峡国际马拉松”比赛，甲乙两运动员相约晨练跑步．甲比乙早分钟跑步出门，分钟后他们相遇．两人寒暄分钟后，决定进行同向跑步练习，练习时甲的速度是米/分，乙的速度是米/分．练习分钟后，乙突感身体不适，于是他按原路以出门时的速度返回，直到与甲再次相遇．如图是甲、乙之间的距离（千米）与甲跑步所用时间（分钟）之间的函数图象．问甲从他家出发到他们再次相遇时，一共用了____________分钟．

18．如图，点P是正方形ABCD边AB上一点，连接PD并将线段PD绕点P顺时针方向旋转得到线段PE，PE交边BC于点F，连接BE、DF．如果AB=2，PF平分，则BF=_______．


三、解答题
19．（1）解方程：；
（2）求抛物线的顶点坐标．
20．为了解九年级学生的体能状况，从我县某校九年级学生中随机抽取部分学生进行八百米跑体能测试，测试结果分为A、B、C、D四个等级，请根据两幅统计图中的信息回答下列问题；
(1)求本次测试共调查了多少名学生？并在答题卡上补全条形统计图；
(2)经测试，全年级有4名学生体能特别好，其中有1名女生，学校准备从这4名学生中任选两名参加运动会，请用列表或画树状图的方法求出女生被选中的概率.

21．已知代数式．
（1）化简已知代数式；
（2）若满足，求已知代数式的值．
22．如图，在平面直角坐标系中，一次函数的图象与二次函数的图象交于第一、二象限内的A，B两点，与轴交于点C．过点B作轴，垂足为M， ，，点A的纵坐标为．

（1）求该二次函数和一次函数的解析式；
（2）连接MC，AO，求四边形CMOA的面积．
23．某水果商今年12月份用元在我县后溪镇某果园购进A种柑橘箱和种柑橘箱．已知A种柑橘的售价是B种柑橘售价的倍少元，预计当月即可全部售完．
（1）该水果商想通过本次销售至少盈利元，则B种柑橘每箱至少卖多少元？
（2）若A、B两种柑橘在（1）的条件下均以最低价格销售，但在实际销售中，受市场影响，A种柑橘的销量还是下降了，售价下降了；B种柑橘的销量下降了，但售价不变，结果A、B两种柑橘的销售总额相等，求的值．
24．在中，，点D是BC上一点，连接AD．
（1）如图1，若，求AD的长；
（2）如图2，延长AC到点E，使，连接BE，将线段BE绕点E顺时针方向旋转一定角度得线段EF，连接FD并延长交AC于点G，且点G是线段AE的中点．求证：．

25．对任意一个三位数t，如果t满足各数位上的数字互不相同，且都不为零，那么称这个数为“互异数”，将一个“互异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与的商记为．例如t，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和与的商为，所以．
（1）计算：；
（2）若都是“互异数”，其中，（，，x，y都是正整数），当时，求的值．
26．如图，在平面直角坐标系中，抛物线y＝﹣x2+4x+5与y轴交于点A，与x轴的正半轴交于点C．
(1)求直线AC解析式；
(2)过点A作AD平行于x轴，交抛物线于点D，点F为抛物线上的一点(点F在AD上方)，作EF平行于y轴交AC于点E，当四边形AFDE的面积最大时？求点F的坐标，并求出最大面积；
(3)若动点P先从(2)中的点F出发沿适当的路径运动到抛物线对称轴上点M处，再沿垂直于y轴的方向运动到y轴上的点N处，然后沿适当的路径运动到点C停止，当动点P的运动路径最短时，求点N的坐标，并求最短路径长.



参考答案
1．A
【分析】
根据坐标系中关于原点对称的点的坐标关系判断即可．
【详解】
解：∵关于原点对称的一组坐标横纵坐标互为相反数，
∴(-2，-3)关于原点对称的点是(2，3) ．
故选：A．
【点睛】
本题主要考查坐标系中关于原点对称的点的坐标关系，熟练掌握坐标系中关于原点对称的点的坐标特征是解题的关键．
2．D
【详解】
解：是轴对称图形，不是中心对称图形，故不符合题意；
既是轴对称图形，又是中心对称图形，故不符合题意；
是轴对称图形，不是中心对称图形，故不符合题意；
不是轴对称图形，是中心对称图形，故符合题意；
故选．
3．C
【分析】
移项，分解因式，即可得出两个一元一次方程，求出方程的解即可．
【详解】
移项得x2-2x=0，
x（x-2）=0，
x=0，x-2=0，
x1=0，x2=2，
故选C．
【点睛】
本题考查了解一元二次方程的应用，解此题的关键是能把一元二次方程转化成一元一次方程，题目比较好，难度适中．
4．D
【分析】
根据题中描述的事件发生的可能性大小，进行判断得出正确答案．
【详解】
“射击运动员射击一次，命中靶心”，可能会命中靶心，也可能不会命中靶心，
这个事件是随机事件．
故选：D．
【点睛】
本题考查随机事件，理解并掌握确定事件、必然事件、不可能事件、随机事件的概念是解题关键．
5．D
【分析】
已知抛物线解析式为顶点式，由y=a（x-h）2+k的对称轴是直线x=h可得答案．
【详解】
解：∵为抛物线的顶点式，
抛物线的对称轴是直线，
故选：D．
【点睛】
本题考查了二次函数的性质，解析式化为顶点式y=a（x-h）2+k，顶点坐标是（h，k），对称轴是直线x=h．
6．B
【分析】
先求出球的所有个数与红球的个数，再根据概率公式解答即可．
【详解】
解：解：共6球在袋中，其中4个红球，
故摸到红球的概率为，
故选：B．
【点睛】
本题考查了概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P(A)= ，难度适中．
7．C
【分析】
先根据圆周角定理求出∠ADB的度数，再由直角三角形的性质求出∠A的度数，进而可得出结论．
【详解】
解：连接AD，
∵AB是⊙O的直径，
∴∠ADB=90°．
∵∠ABD=55°，
∴∠DAB=90°-55°=35°，
∴∠BCD=∠DAB=35°．
故选：C．

【点睛】
本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．
8．C
【分析】
根据圆周角定理得∠BOC＝2∠A＝45°，由于⊙O的直径AB垂直于弦CD，根据垂径定理得CE＝DE，且可判断△OCE为等腰直角三角形，设OE=CE=x，根据勾股定理可求得CE的长，然后利用CD＝2CE进行计算．
【详解】
∵直径AB垂直于弦CD，
∴CE=DE=CD，
∵∠A=22.5°，
∴∠BOC=45°，
∴OE=CE，
设OE=CE=x，
∵OC=4，
∴x2+x2=16，
解得：x=2，
即：CE=2，
∴CD=4，
故选C．
【点睛】
本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等腰直角三角形的性质和垂径定理．
9．A
【详解】
考点：旋转的性质．
分析：已知旋转角度，旋转方向，可求∠A′CA，根据互余关系求∠A′，根据对应角相等求∠BAC．
解：依题意旋转角∠A′CA=40°，
由于AC⊥A′B′，由互余关系得∠A′=90°-40°=50°，
由对应角相等，得∠BAC=∠A′=50°．故选A．
10．D
【分析】
可先表示出第一次降价后的价格，那么第一次降价后的价格×（1﹣降低的百分率）＝16，把相应数值代入即可求解．
【详解】
解：设该药品平均每次降价的百分率是x，则第一次降价后的价格为30×（1﹣x）元，
第二次降价后的售价是在第一次降价后的价格的基础上降低x，为30×（1﹣x）×（1﹣x）元，则列出的方程是．
故选：D．
【点睛】
本题考查了由实际问题抽象出一元二次方程：求平均变化率．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a(1±x)2=b．
11．B
【分析】
本题考查找规律，第n个图的正中间有（2n-1）个圆，向上依次减少2个圆，向下依次减少 1个圆．
【详解】
观察题图可知，图①中有1个圆；
图②中有（1+3+2）个圆，一共有 6 个小圆；
图③中有（1+3+5+4+3）个圆，一共有 16 个小圆；
图④中有 （1+3+5+7+6+5+4）个圆，一共有31个圆；
图⑤中有（1+3+5+7+9+8+7+6+5）个圆，一共有51个圆；
图⑥中有（1+3+5+7+9+11+10+9+8+7+6+5+4）个圆，一共有76个圆．
故选B．
【点睛】
此题考查了据图形归纳数字规律的问题，关键是通过观察图形归纳出数字规律．
12．A
【分析】
要使得关于的一元二次方程有解，利用根的判别式求出符合条件的值，再解方程，解出a的可能值，最终综合选择满足所有条件的a的值，然后求它们的和即可．
【详解】
解：要使得关于的一元二次方程有解，
则Δ≥16-4×（-2a）≥0，
解得a≥-2,
∴a的可能值为-2，-1、0、1、2，
解可得，
，



使得方程有整数解满足条件的a的值为0、2，
综上所述满足条件的a的值为0、2，
0+2=2，
故选：A．
【点睛】
本题考查了根的判别式以及分式方程，灵活运用根的判别式以及熟练求解分式方程是解题的关键．
13．向下
【分析】
二次函数的二次项系数a＜0，则抛物线开口向下．
【详解】
解：抛物线中，
∵a=-3＜0，
∴开口向下，
故答案为：向下．
【点睛】
本题考查了二次函数的性质，解题的关键是熟悉二次函数的图象与系数之间的关系．本题属于基础题，难度不大，解决该题型题目时，熟练掌握二次函数的图象与系数之间的关系是关键．
14．
【分析】
答对的一种情况除以总情况数4即为所求的概率．
【详解】
根据概率公式P（A）=，
得答对的概率为P（A）==．
【点睛】
如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．熟练掌握是解决问题的关键．
15．60
【分析】
直接利用二次函数的性质求出二次函数对称轴，即可得出答案．
【详解】
由题意知
当t=- = =60（秒）时，s取得最大值，
即飞机着陆后滑行到停止的时间为60秒．
故答案为60秒
【点睛】
本题主要考查了二次函数的应用，正确求出二次函数对称轴是解题关键．
16．
【详解】
解：在矩形ABCD中，∵AB=4，BC=2，∴AB=2DA，AB=AE（扇形的半径），∴AE=2DA，∴∠AED=30°，∴∠1=90°﹣30°=60°．∵DA=2，∴AB=2DA=4，∴A E=4，∴DE= =，∴阴影FDE的面积S1=S扇形AEF﹣S△ADE=﹣×2×= ．
阴影ECB的面积S2=S矩形﹣S△ADE﹣S扇形ABE=2×4﹣×2×﹣=；
则图中阴影部分的面积为=+ =．
故答案为．
点睛：本题考查了矩形的性质，扇形的面积计算，直角三角形30°角所对的直角边等于斜边的一半的性质，熟记性质并求出∠AED=30°是解题的关键，也是本题的难点．
17．11
【分析】
由图象可以看出，0-1min内，甲的速度可由距离减小量除以时间求得，1-3min内，根据等量关系“距离减小量=甲跑过的路程+乙跑过的路程”可得出乙的速度；由于甲的速度始终是180米/分，乙的速度开始是240米/分，则他们的速度之差是60米/分，则5分钟相差400米，设再经过t分钟两人相遇，利用相遇问题得到180t+120t=400，然后求出t后加上前面的10分钟可得到小刚从家出发到他们再次相遇的时间总和．
【详解】
甲出门时的速度v1=（540-440）=100（米/分），
设乙出门时的速度为v2（米/分），
根据题意得2×（v1+v2）=440，解得v2=120米/分，
甲的速度始终是180米/分，乙的速度开始为240米/分，他们的速度之差是60米/分，5分钟相差300米，
设再经过t分钟两人相遇，则180t+120t=300，解得t=1（分）
所以甲从家出发到他们再次相遇时5+5+1=11（分）．
故答案为：11．
【点睛】
本题考查了一次函数的应用：会利用一次函数图象解决行程问题的数量关系，相遇问题，追击问题的综合应用；解答时灵活运用行程问题的数量关系解答是关键．
18．
【分析】
如下图所示，过点P作DE的垂线交于点G，则，得到，再进一步证明，得到，则点P是AB的中点，且AB=2，得到AP=PB=1，通过△PBF∽△DAP，即可得到结果．
【详解】
解：过点P作DE的垂线交于点G，

∵PF平分，，,
∴，，
在和中，

∴≌（AAS）
∴，
又∵PD绕点P顺时针方向旋转得到线段PE，
∴，
∴，
由直角三角形中的互余关系可得，
，
在和中，

∴≌（AAS）
∴，
则，
∵AB=2，
∴AP=PB=1，
∵FB⊥AB，DA⊥AB，
∴，
又∵
∴△PBF∽△DAP，
∴，
∵PB=AP=1，DA=2，
∴BF=．
故答案为：．
【点睛】
本题主要考查了全等三角形以及相似三角形的判定与性质，利于互余关系推导出三角形全等与相似是解题的关键．
19．（1）；（2）
【分析】
（1）已知的一元二次方程为一般式，直接利用公式法写出一元二次方程的解即可；
（2）已知抛物线的解析式是一般式，根据抛物线的顶点坐标公式，直接计算出其顶点坐标即可；
【详解】
解：（1）
，
，
；
（2），　，
该抛物线的顶点为．
【点睛】
本题考查了解一元二次方程的公式法和二次函数的顶点坐标公式，一元二次方程，当时，其解为；抛物线，其顶点坐标为（，），理解并熟记公式是解本题的关键．
20．(1)共调查了50名学生，补图见解析；(2).
【分析】
（1）设本次测试共调查了名学生，根据总体、个体、百分比之间的关系列出方程即可解决.用总数减去、、中的人数，即可解决，画出条形图即可.
（2）画树状图展示所有12种等可能的结果数，再找出恰好抽到有1名女生的结果数，然后根据概率公式计算.
【详解】
解：(1)设本次测试共调查了名学生.
由题意，
解得：
∴本次测试共调查了50名学生.
则测试结果为等级的学生数＝人.
条形统计图如图所示，

(2)画树状图：

共有12种等可能的结果数，其中恰好抽到有1名女生的结果数6，
所以恰好抽到有1名女生的概率＝＝.
【点睛】
本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果，再从中选出符合事件或的结果数目，然后利用概率公式计算事件或事件的概率．也考查了统计图．解题的关键是灵活运用这些知识解决问题．
21．（1）；（2）
【分析】
（1）先将分子分母因式分解，再算括号内，再算除法，即可求解；
（2）根据分式有意义的条件，可得，再根据，即可求解．
【详解】
解：（1）原式＝
＝
＝
＝
＝；
（2）由已知得，由知：
，即，
所以原式．
【点睛】
本题主要考查了分式的化简求值，分是有意义的条件，二次根式的化简，熟练掌握分式化简的基本步骤是解题的关键．
22．（1），；（2）3
【分析】
（1）根据题意，得出交点B的坐标，带入二次函数解析式，求出二次函数解析式；根据二次函数解析式求出A点坐标，再将A、B两点坐标带入一次函数解析式求解即可；
（2）分别求出与，四边形的面积即为两个三角形面积之和．
【详解】
（1）∵BMx轴，垂足为M，
∴∠BMO=90°，
∵BM=OM，OB=，
∴BM=OM =1，
∴点B的坐标为（-1，1）．
把B（-1，1）代入得：，
∴，
∴二次函数的解析式为．
∵点A在的图象上，点A的纵坐标为4，
∴，即，
∵点A在第一象限，则．
把、B（-1，1）代入得：
，解得
∴一次函数的解析式为；
（2）在中，得点C的坐标为（0，2），
∴．
∴．
【点睛】
本题考查了一次函数与二次函数的交点问题，利用交点坐标坐标进行求解．熟练掌握是解决问题的关键．
23．（1）B种柑橘每箱至少卖50元；（2）20
【分析】
（1）设每箱B柑橘卖x元，则A柑橘每箱卖（2x-10）元，根据“A、B两种柑橘的总销售额-总成本≥8000”列不等式求解可得；
（2）根据“A柑橘下降后的销量×下降后的售价=B柑橘下降后的销量×售价”列出方程求解可得．
【详解】
解：（1）设B种柑橘每箱卖x元．由题意，得：
250（2x－10）＋150x－22000≥8000，
解得 x≥50，
答：B种柑橘每箱至少卖50元；
（2）根据题意，得，
设，化简得 ．
解得 ， (不合题意，舍去)
，
答：m的值为20．
【点睛】
本题主要考查一元二次方程和一元一次不等式的应用，理解题意找到相等和不等关系列出方程或不等式是解题的关键．
24．（1）；（2）见解析
【分析】
（1）由等腰直角三角形的性质计算得到，再由勾股定理可得AD的长；
（2）先证明≌，得到，进而得到，再运用倍长中线法，延长到，使，连接,证明≌，得到进而得到，从而得证；
【详解】
(1)解⊥，　．∴是直角三角形，
，
在中，由勾股定理得：
；
（2）证明：⊥，，

≌

是由绕点旋转得到的，

延长到，使，连接,
∵点是的中点，
，
≌,

，
．

【点睛】
本题主要考查了全等三角形的判定和性质、等腰三角形的判定和性质、旋转的性质、等腰直角三角形的性质及勾股定理得运用，解题的关键是利用倍长中线法，构造全等三角形和．
25．（1），；（2）48
【分析】
（1）根据相异数的概念首先写出对调的三个数，再求和，计算F(621)，F(518)即可；
（2）首先根据题意计算F（m）和F（n），求解x和y的值即可．
【详解】
解：（1），
；
m，n都是“互异数”， ，
，
，
∵，
∴
∴，
∵，，x，y都是正整数，
∴，，
∵m，n都是“互异数”，
∴．
∴，，
∴或，
故或
【点睛】
本题主要考查新概念的理解，根据新概念列方程，采用分类讨论的思想求解.
26．(1)y＝﹣x+5；(2)点F(，)；四边形AFDE的面积的最大值为；(3)点N(0，)，点P的运动路径最短距离＝2+.
【分析】
(1)先求出点A，点C坐标，用待定系数法可求解析式；
(2)先求出点D坐标，设点F(x，﹣x2+4x+5)，则点E坐标为(x，﹣x+5)，即可求EF＝﹣x2+5x，可求四边形AFDE的面积，由二次函数的性质可求解；
(3)由动点P的运动路径＝FM+MN+NC＝GM+2+MH，则当点G，点M，点H三点共线时，动点P的运动路径最小，由两点距离公式可求解.
【详解】
解：(1)∵抛物线y＝﹣x2+4x+5与y轴交于点A，与x轴的正半轴交于点C.
∴当x＝0时，y＝5，则点A(0，5)
当y＝0时，0＝﹣x2+4x+5，
∴x1＝5，x2＝﹣1，
∴点B(﹣1，0)，点 C(5，0)
设直线AC解析式为：y＝kx+b，
∴
解得：
∴直线AC解析式为：y＝﹣x+5，
(2)∵过点A作AD平行于x轴，
∴点D纵坐标为5，
∴5＝﹣x2+4x+5，
∴x1＝0，x2＝4，
∴点D(4，5)，
∴AD＝4
设点F(x，﹣x2+4x+5)，则点E坐标为(x，﹣x+5)
∴EF＝﹣x2+4x+5﹣(﹣x+5)＝﹣x2+5x，
∵四边形AFDE的面积＝AD×EF＝2EF＝﹣2x2+10x＝﹣2(x﹣)2+
∴当x＝时，四边形AFDE的面积的最大值为，
∴点F(，)；
(3)∵抛物线y＝﹣x2+4x+5＝﹣(x﹣2)2+9，
∴对称轴为x＝2，
∴MN＝2，
如图，将点C向右平移2个单位到点H(7，0)，过点F作对称轴x＝2的对称点G(，)，连接GH，交直线x＝2于点M，

∵MN∥CH，MN＝CH＝2，
∴四边形MNCH是平行四边形，
∴NC＝MH，
∵动点P的运动路径＝FM+MN+NC＝GM+2+MH，
∴当点G，点M，点H三点共线时，动点P的运动路径最小，
∴动点P的运动路径最短距离＝2+＝2+，
设直线GH解析式为：y＝mx+n，
∴，
解得，
∴直线GH解析式为：y＝﹣x+，
当x＝2时，y＝，
∴点N(0，).
【点睛】
此题是二次函数综合题，主要考查了待定系数法求解析式，函数极值的确定方法，两点距离公式等知识，解题的关键是学会利用对称解决最短问题．