河北省秦皇岛市卢龙县2020-2021学年八年级下学期期末数学试题（word版 含答案）

这是一份河北省秦皇岛市卢龙县2020-2021学年八年级下学期期末数学试题（word版 含答案），共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
河北省秦皇岛市卢龙县2020-2021学年八年级下学期期末数学试题
学校:___________姓名：___________班级：___________考号：___________


一、单选题
1．一辆汽车以50的速度行驶,行驶的路程与行驶的时间之间的关系式为,其中变量是（ ）
A．速度与路程 B．速度与时间 C．路程与时间 D．速度
2．矩形是轴对称图形，对称轴可以是（ ）

A． B． C． D．
3．正比例函数y=3x的大致图像是( )
A． B． C． D．
4．下列调查:①了解夏季冷饮市场上冰淇淋的质量;②了解嘉淇同学20道英语选择题的通过率;③了解一批导弹的杀伤范围；④了解全国中学生睡眠情况.不适合普查而适合做抽样调查的是（ ）
A．①②④ B．①③④ C．②③④ D．①②③
5．若y=x+2–b是正比例函数，则b的值是( )
A．0 B．–2 C．2 D．–0.5
6．下面条件中，能判定四边形是平行四边形的条件是（ ）
A．一组对角相等 B．对角线互相平分 C．一组对边相等 D．对角线互相垂直
7．如果点P（2，b）和点Q（a，﹣3）关于x轴对称，则a+b的值是（　　）
A．﹣1 B．1 C．﹣5 D．5
8．若一次函数y=kx+b的图象如图所示，则函数y=﹣3kx﹣b的图象可能为（　　）

A． B．
C． D．
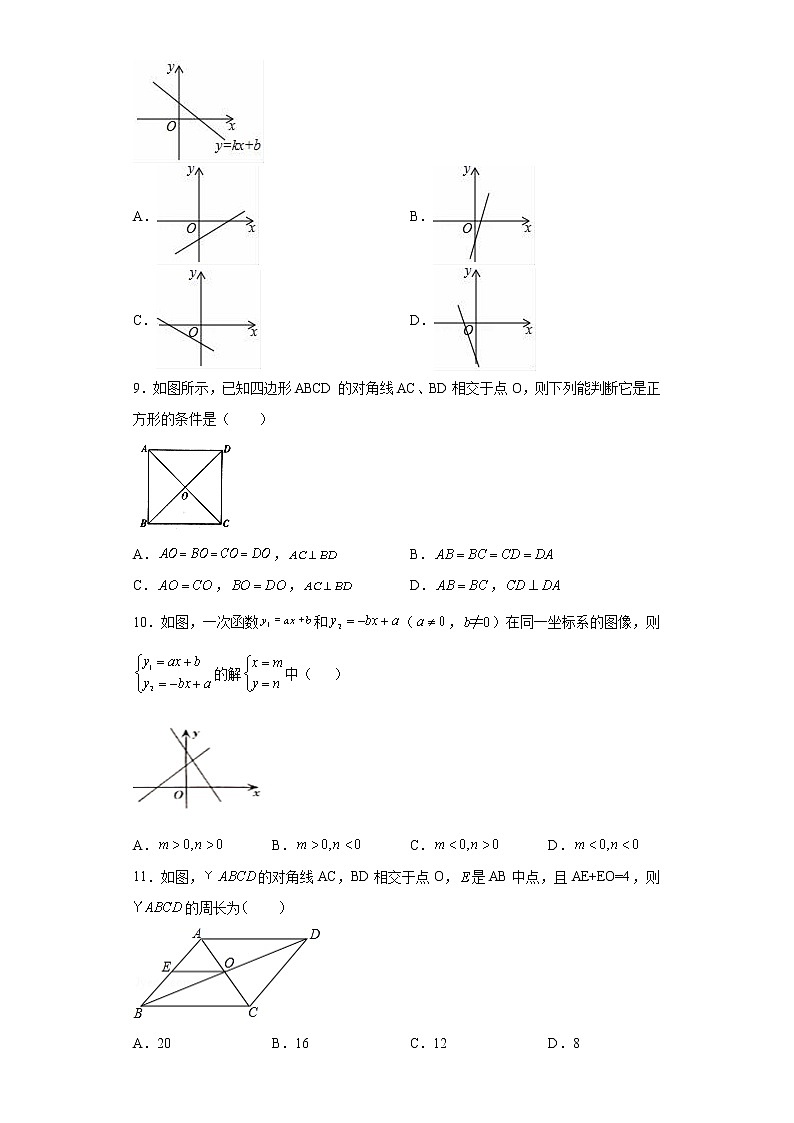
9．如图所示，已知四边形ABCD的对角线AC、BD相交于点O，则下列能判断它是正方形的条件是（ ）

A．， B．
C．，， D．，
10．如图，一次函数和（，）在同一坐标系的图像，则的解中（ ）

A． B． C． D．
11．如图，的对角线AC，BD相交于点O，是AB中点，且AE+EO=4，则的周长为　　

A．20 B．16 C．12 D．8
12．在平面直角坐标系中，把点P先向左平移7个单位长度，再向上平移5个单位长度得到点M，作点M关于y轴的对称点N．已知点N的坐标是(5，1)，那么点P的坐标是 ( 　　)
A．(2，-4) B．(6，-4) C．(6，-1) D．(2，-1)
13．如图，一次函数的图象与两坐标轴分别交于A，B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长是（　　）

A．5 B．7.5 C．10 D．25
14．如图，△ABC的周长为10，BC=x，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC分别交AB，AC于点E，F，若设△AEF的周长为y，则y与x之间的函数关系图像大致是 ( 　 　)

A． B． C． D．

二、填空题
15．点到轴的距离为_______．
16．函数中自变量的取值范围是______________．
17．如图，∠1，∠2，∠3是五边形ABCDE的3个外角，若，则________.

18．如图，在四边形ABCD中，AB=CD，再添加一个条件________（写出一个即可），可使四边形ABCD是平行四边形．（图形中不再添加辅助线）

19．学校位于小亮家北偏东35方向，距离为300m，学校位于大刚家南偏东85°方向，距离也为300m，则大刚家相对于小亮家的位置是________.
20．如图，小明从点出发，前进5 m后向右转20°，再前进5m后又向右转20°，这样一直走下去，直到他第一次回到出发点为止，他所走的路径构成了一个多边形，则这个多边形的内角和是_________度．


三、解答题
21．根据下列条件分别确定函数的解析式：
（1）与成正比例，当时，；
（2）直线经过点和点．
22．某校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．


（1）这次被调查的同学共有　 　人；
（2）补全条形统计图，并在图上标明相应的数据；
（3）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐．据此估算，该校3800名学生一餐浪费的食物可供多少人食用一餐．
23．某气象研究中心观测一场沙尘暴从发生到结束全过程，开始时风暴平均每小时增加2千米/时，4小时后，沙尘暴经过开阔荒漠地，风速变为平均每小时增加4千米/时，一段时间，风暴保持不变，当沙尘暴遇到绿色植被区时，其风速平均每小时减小1千米/时，最终停止．结合风速与时间的图象，回答下列问题：
（1）在y轴内填入相应的数值；
（2）沙尘暴从发生到结束，共经过　 小时？
（3）求出当x≥25时，风速y（千米/时）与时间x（小时）之间的函数关系式；

24．
如图，四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点.

⑴请判断四边形EFGH的形状？并说明为什么.
⑵若使四边形EFGH为正方形，那么四边形ABCD的对角线应具有怎样的性质？
25．如图，已知四边形中，对角线相交于点，且，，过点作，分别交于点.

(1)求证: ；
(2)判断四边形的形状，并说明理由.
26．如图，在平面直角坐标系中，直线过点且与轴交于点，把点向左平移2个单位，再向上平移4个单位，得到点.过点且与平行的直线交轴于点.

（1）求直线的解析式；
（2）直线与交于点，将直线沿方向平移，平移到经过点的位置结束，求直线在平移过程中与轴交点的横坐标的取值范围.


参考答案
1．C
【分析】
在函数中，给一个变量x一个值，另一个变量y就有对应的值，则x是自变量，y是因变量，据此即可判断．
【详解】
解：由题意的：s=50t，路程随时间的变化而变化，则行驶时间是自变量，行驶路程是因变量；
故选C．
【点睛】
此题主要考查了自变量和因变量，正确理解自变量与因变量的定义，是需要熟记的内容．
2．D
【分析】
根据轴对称图形的概念求解．矩形是轴对称图形，可以左右重合和上下重合．
【详解】
解：矩形是轴对称图形，可以左右重合和上下重合，
故可以是矩形的对称轴，
故选D.
【点睛】
此题主要考查了轴对称的概念，轴对称的关键是寻找对称轴，两边图象折叠后可重合．
3．B
【详解】
∵3>0,
∴图像经过一、三象限.
故选B.
点睛：本题考查了正比例函数图象与系数的关系：对于y=kx，当k＞0时， y=kx的图象经过一、三象限；当k＜0时， y=kx的图象经过二、四象限.
4．B
【分析】
调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来，考查会给被调查对象带来损伤破坏，以及考查经费和时间都非常有限时，普查就受到限制，这时就应选择抽样调查．
【详解】
解：①④中个体数量多，范围广，工作量大，不宜采用普查，只能采用抽样调查；
③了解一批导弹的杀伤范围具有破坏性不宜普查；
②个体数量少，可采用普查方式进行调查.
故选B．
【点睛】
本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
5．C
【分析】
根据正比例函数的定义可得关于b的方程，解出即可．
【详解】
解：由正比例函数的定义可得：2-b=0，
解得：b=2．
故选C．
【点睛】
考查了正比例函数的定义，解题关键是掌握正比例函数的定义条件：正比例函数y=kx的定义条件是：k为常数且k≠0，自变量次数为1．
6．B
【分析】
根据平行四边形判定定理判断即可．
【详解】
∵一组对角相等的四边形不是平行四边形,
∴A错误；
∵对角线互相平分的四边形是平行四边形,
∴B正确；
∵一组对边相等的四边形不是平行四边形,
∴C错误；
∵对角线互相垂直的四边形不是平行四边形,
∴D错误；
故选B．
【点睛】
本题考查了平行四边形的判定定理，熟练掌握平行四边形的判定定理是解题的关键．
7．D
【分析】
直接利用关于x轴对称点的性质得出a，b的值，进而得出答案．
【详解】
解：∵点P（2，b）和点Q（a，﹣3）关于x轴对称，
∴a＝2，b＝3，则a+b的值是5．
故选：D．
【点睛】
本题考查轴对称相关，熟练掌握轴对称的相关性质是解题关键.
8．B
【分析】
根据是一次函数y=kx+b的图象经过一、二、四象限得出k，b的取值范围解答即可．
【详解】
因为一次函数y=kx+b的图象经过一、二、四象限，
可得：k0，
所以直线y=﹣3kx﹣b的图象经过一、三、四象限，
故答案选B.
【点睛】
本题考查了一次函数图象与系数的关系，解题的关键是熟练的掌握一次函数图象与系数的关系.
9．A
【分析】
根据正方形的判定定理即可求解.
【详解】
A∵，∴四边形ABCD为矩形，
由，所以矩形ABCD为正方形，
B. ，四边形ABCD为菱形；
C. ，，，四边形ABCD为菱形；
D. ，，不能判定四边形ABCD为正方形,
故选A.
【点睛】
此题主要考查正方形的判定，解题的关键是熟知正方形的判定定理.
10．A
【分析】
方程组的解就是一次函数y1=ax+b和y2=-bx+a（a≠0，b≠0）图象的交点，根据交点所在象限确定m、n的取值范围.
【详解】
解：方程组的解就是一次函数y1=ax+b和y2=-bx+a（a≠0，b≠0）图象的交点，
∵两函数图象交点在第一象限，
∴m＞0，n＞0，
故选A．
【点睛】
此题主要考查了一次函数与二元一次方程组的解，关键是掌握两函数图象的交点就是两函数解析式组成的方程组的解．
11．B
【分析】
首先证明：OE=BC，由AE+EO=4，推出AB+BC=8即可解决问题；
【详解】
∵四边形ABCD是平行四边形，
∴OA=OC，
∵AE=EB，
∴OE=BC，
∵AE+EO=4，
∴2AE+2EO=8，
∴AB+BC=8，
∴平行四边形ABCD的周长=2×8=16，
故选B．
【点睛】
本题考查平行四边形的性质、三角形的中位线定理等知识，解题的关键是熟练掌握
三角形的中位线定理，属于中考常考题型．
12．A
【分析】
先根据点的关于y轴对称性质由N点求出点M，再根据点的平移性质求出点P.
【详解】
解：因为点M和点N关于y轴对称，N点坐标是（5，1），
所以点M是（-5，1），
又因为点P先向左平移7个单位长度，再向上平移5个单位长度得到点M，
所以点P是（2，-4），
故选A.
【点睛】
本题主要考查点的对称和点的平移，解决本题的关键是要熟练掌握点的对称性质和点的平移性质.
13．C
【详解】
∵A（5，0），B（0，5），
∴直线AB的解析式为y=﹣x+5，
∵P是线段AB上任意一点（不包括端点），
∴设P点坐标为（m，﹣m+5），
如图，过P点分别作PD⊥x轴，PC⊥y轴，垂足分别为D、C，

∵P点在第一象限，
∴PD=﹣m+5，PC=m，
∴矩形PDOC的周长为：2（m﹣m+5）=10，
故选C．
14．B
【分析】
首先证明BE＝OE，CF＝OF，得出△AEF的周长y与x的关系式为y＝10﹣x，求出0＜x＜5，即可求得答案．
【详解】
解：∠ABC和∠ACB的平分线相交于点O，
∴∠ABO＝∠CBO，∠ACO＝∠BCO，
∵EF∥BC，
∴∠EOB＝∠CBO，∠FOC＝∠BCO，
∴∠ABO＝∠EOB，∠ACO＝∠FOC,
∴BE＝OE，CF＝OF，
∴△AEF的周长y＝AE＋EF＋AF＝AE＋OE＋OF＋AF＝AB＋AC，
∵△ABC的周长为10，BC＝x，
∴AB＋AC＝10﹣x，
∴y＝10﹣x，
∵AB＋AC＞BC
∴y＞x，
∴10﹣x＞x，
∴0＜x＜5，
即y与x的函数的关系式为：y＝10﹣x（0＜x＜5），
故选；B．
【点睛】
本题考查动点问题的函数图象、平行线的性质、等腰三角形的判定、三角形的周长等知识点；求出y与x的关系式是解决问题的关键．
15．4
【分析】
求得-4的绝对值即为点A到x轴的距离．
【详解】
解：∵点A到x轴的距离为其纵坐标的绝对值即|-4|=4，
∴点A到x轴的距离为4．
故答案为：4
【点睛】
考查了点的坐标，用到的知识点为：点到x轴的距离为点的纵坐标的绝对值．
16．x＜4
【分析】
根据二次根式的意义，被开方数是非负数，以及分母不等于0即可求解．
【详解】
解：根据题意得4-x＞0，
解得x＜4．
故答案为：x＜4．
【点睛】
本题考查了函数自变量的取值范围的确定和分式的意义．函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负数．
17．220
【分析】
先求出∠A与∠B的外角和，再根据外角和进行求解.
【详解】
∵
∴∠A与∠B的外角和为360°-220°=140°，
∵∠1，∠2，∠3是五边形ABCDE的3个外角，
∴360°-140°=220°，
故填：220°.
【点睛】
此题主要考查多边形的外角，解题的关键是熟知多边形的外角和为360°.
18．ABCD或AD=BC
【分析】
可再添加一个条件AD＝BC或ABCD，根据平行线的判定定理即可求解．
【详解】
解：根据平行四边形的判定，可再添加一个条件：AD＝BC或ABCD
故答案为：ABCD或AD=BC．
【点睛】
此题主要考查平行四边形的判定．是一个开放条件的题目，熟练掌握判定定理是解题的关键．
19．北偏西25°方向距离为300m
【分析】
根据题意作出图形，即可得到大刚家相对于小亮家的位置.
【详解】
如图，根据题意得∠ACD=35°，∠ABE=85°，AC=AB=300m
由图可知∠CBE=∠BCD，
∵AB=AC,
∴∠ABC=∠ACB，
即∠ABE-∠CBE=∠ACD+∠BCD，
∴85°-∠CBE=35°+∠CBE，
∴∠CBE=25°，
∴∠ABC=∠ACB=60°，
∴△ABC为等边三角形，则BC=300m,
∴大刚家相对于小亮家的位置是北偏西25°方向距离为300m
故填：北偏西25°方向距离为300m.

【点睛】
此题主要考查方位角的判断，解题的关键是根据题意作出图形进行求解.
20．2880
【分析】
先根据题意判断该多边形的边数，再运用多边形的内角和公式计算该多边形的内角和即可．
【详解】
解：由题意知，该多边形为正多边形，
∵多边形的外角和恒为360°，
360÷20＝18，
∴该正多边形为正18边形．
这个多边形的内角和为：（18−2）×180°＝2880°，
故答案为：2880．
【点睛】
本题考查了正多边形的相关知识，掌握多边形的内角和公式是解决本题的关键．
21．（1）；（2）
【分析】
（1）设y=mx，当x=2时，y=3时，代入可得m，可得解析式；
（2）将点（3，2）与点（-2，1）的坐标代入解析式可得k，易得一次函数解析式．
【详解】
解：（1）∵y与x成正比例
∴设y=mx
∵当x=2时，y=3
∴3=2m
∴m=
∴所求函数解析式为
（2）∵直线y=kx+b过点（3，2）和点（-2，1）
∴
解得：
∴所求函数解析式为
【点评】
本题主要考查了待定系数法求解析式，将坐标代入解得k，b是关键．
22．（1）1000；（2）见解析；（3）190
【分析】
（1）根据不剩的人数和所占的百分比，可以计算出这次被调查的同学共有多少人；
（2）根据（1）中的结果和条形统计图中的数据，可以计算出剩少量的人数，然后即可将条形统计图补充完整；
（3）根据题意和题目中的数据，可以计算出该校3800名学生一餐浪费的食物可供多少人食用一餐．
【详解】
解：（1）这次被调查的同学共有600÷60%＝1000（人），
故答案为：1000；
（2）剩少量的人数为1000﹣（600+150+50）＝200人，
补全条形图如下：

（3）
答：估计该校18000名学生一餐浪费的食物可供190人食用一餐．
【点睛】
本题考查条形统计图、扇形统计图、用样本估计总体，利用数形结合的思想解答是解答本题的关键．
23．（1）8，32；（2）57；（3）y=-x+57（25≤x≤57）
【分析】
（1）速度＝增加幅度×时间；
（2）求出沙尘暴从开始减速到停止定的时间＋25小时；
（3）根据待定系数法即可求解一次函数解析式；
【详解】
解：（1）2×4＝8，
则8＋4×（10−4）＝32；
故答案为：8；32；
（2）依题意可得沙尘暴从发生到结束，共经过32÷1＋25＝57小时；
故答案为：57；
（3）根据图象，CD经过（25，32）（57，0），
设函数解析式为y＝kx＋b，
∴，解得，
∴y＝−x＋57（25≤x≤57）．
【点睛】
此题主要考查一次函数的实际应用，解题的关键是熟知待定系数法的运用．
24．（1）四边形EFGH是平行四边形，理由见解析；（2）AC=BD且AC⊥BD
【分析】
（1）连接四边形的对角线，根据题目所给四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，可得四边形对边平行且相等，从而判断平行四边形；
（2）只要加对角线相等且互相垂直就可证明是正方形；
【详解】
解：（1）∵E是AB的中点，H是AD的中点，
∴EH//BD，EH= BD，
∵F是BC的中点，G是CD的中点，
∴GF//BD，GF=BD，
GF//EH，GF=EH，
∴四边形EFGH是平行四边形．
（2）若加AC=BD且AC⊥BD，则四边形EFGH会是正方形，
在（1）的条件下，∵AC=BD，
∴EF=FG=GH=HE，
∴四边形EFGH是菱形．
又∵AC⊥BD，EH∥BD，EF∥AC，
∴∠HEF=90°，
∴四边形EFGH是正方形．

【点睛】
本题考查了平行四边形的判定，三角形的中位线，正方形的判定，熟练掌握平行四边形和正方形的判定方法是解答本题的关键．
25．（1）证明见解析；（2）四边形BED是菱形，理由见解析.
【详解】
【分析】（1）根据对角线互相平分的四边形是平行四边形，由已知可得四边形ABCD是平行四边形，继而可根据ASA证明ΔAOE≌ΔCOF；
（2）由ΔAOE≌ΔCOF可得OE=OF，再根据OB=OD可得四边形BEDF是平行四边形，再根据对角线互相垂直的平行四边形是菱形即可证得四边形BEDF是菱形.
【详解】（1）∵OA=OC，OB=OD，
∴四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAC＝∠BCA，
又∵∠AOE=∠COF，OA=OC，
∴△AOE≌△COF（ASA）；
（2）四边形BEDF是菱形，理由如下：
∵△AOE≌△COF，
∴OE=OF，
又∵OB=OD，
∴四边形DEBF是平行四边形，
又∵EF⊥BD，
∴平行四边形DEBF是菱形.
【点睛】本题考查了平行四边形的判定与性质、菱形的判定，熟记平行四边形的判定与性质定理、菱形的判定定理是解本题的关键.
26．（1）（2）
【分析】
（1）由题意先求出点A的坐标，再根据平移求得点C的坐标，由直线CD与y=2x平行，可设直线CD的解析式为y=2x+b，代入点C坐标利用待定系数法即可得；
（2）先求得点B坐标，根据直线平移后经过点B，可得平移后的解析式为y=2x+3，分别求得直线CD、直线BF与x轴的交点坐标即可得到平移过程中与x轴交点横坐标的取值范围.
【详解】
（1）点在直线上，
，，
又点向左平移2个单位，又向上平移4个单位得到点，
，
直线与平行，
设直线的解析式为，
又直线过点，
∴2=6+b，解得b=-4，
直线的解析式为；
（2）将代入中，得，即，
故平移之后的直线的解析式为，
令，得，即，
将代入中，得，即，
平移过程中与轴交点的取值范围是：.
【点评】
本题主要考查了一次函数的平移，待定系数法等，明确直线平移k值不变是解题的关键.