冀教版八年级上册17.1 等腰三角形图片ppt课件

这是一份冀教版八年级上册17.1 等腰三角形图片ppt课件，共36页。PPT课件主要包含了写一写，动画演示，例题讲解，小试牛刀，能力训练，学以致用看我的，实际应用我能行，能力提高我最棒，思维升级我来画，表彰冠军组等内容，欢迎下载使用。


图中有些你熟悉的图形吗?它们有什么共同特点?
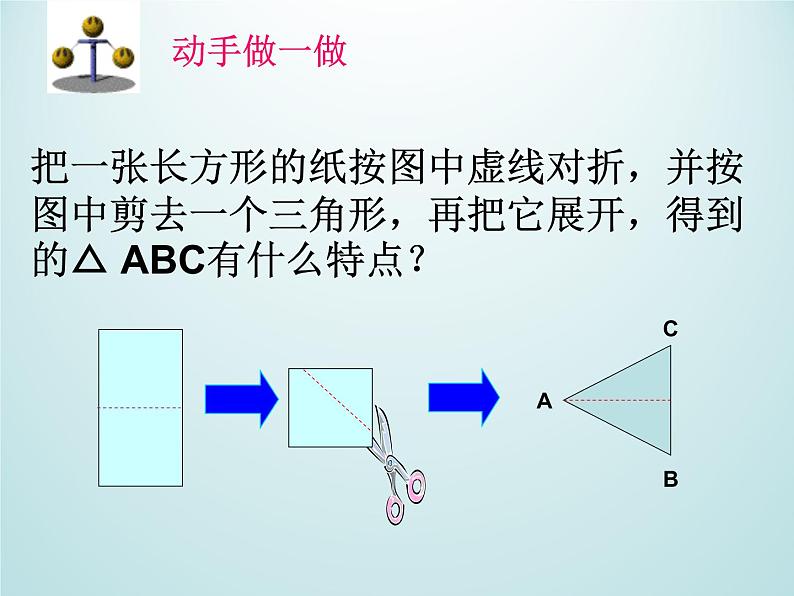
把一张长方形的纸按图中虚线对折，并按图中剪去一个三角形，再把它展开，得到的△ ABC有什么特点？
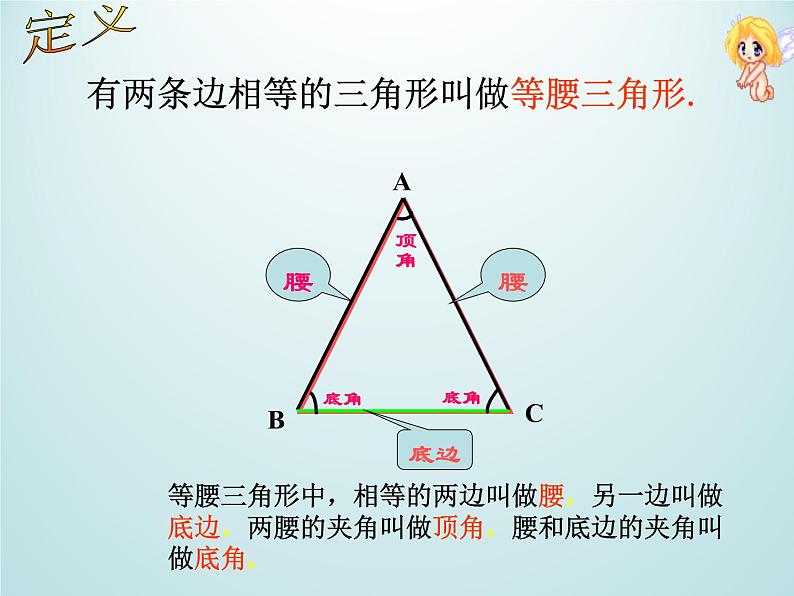
有两条边相等的三角形叫做等腰三角形.
等腰三角形中，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.
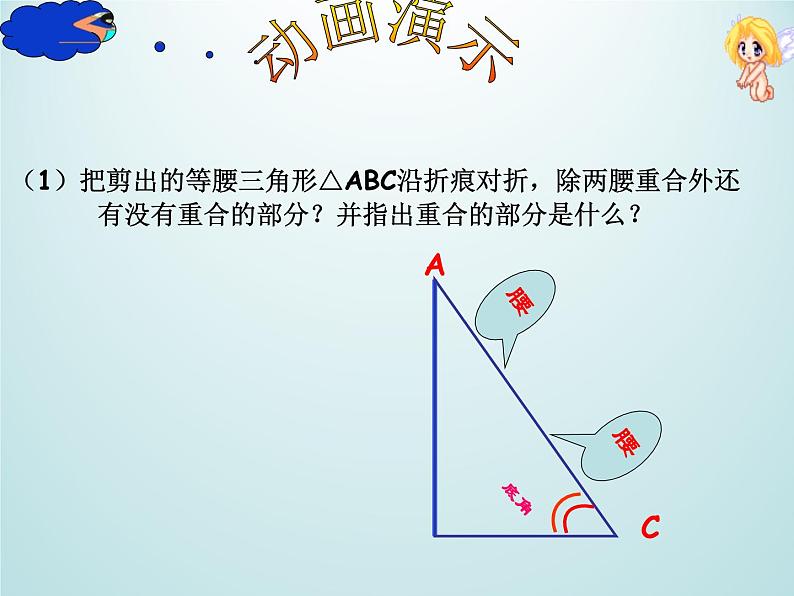
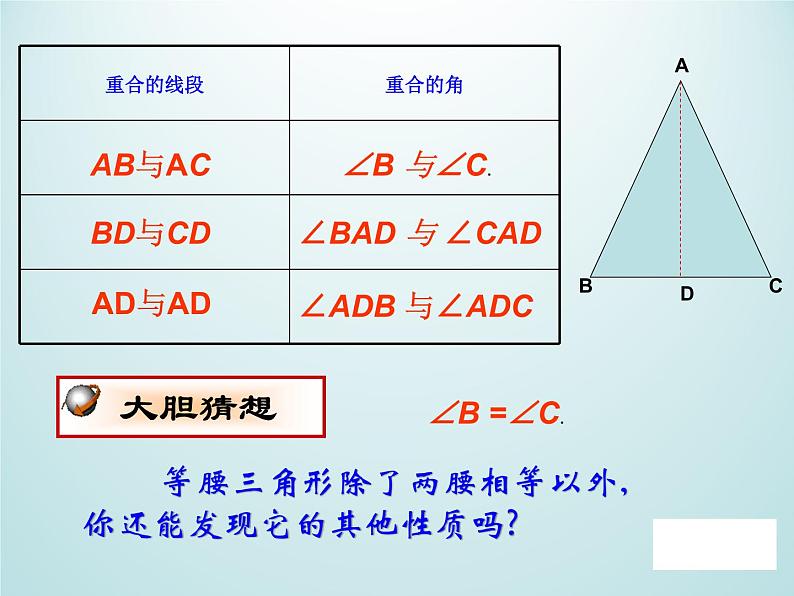
（1）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？
∠BAD 与 ∠CAD
等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗?
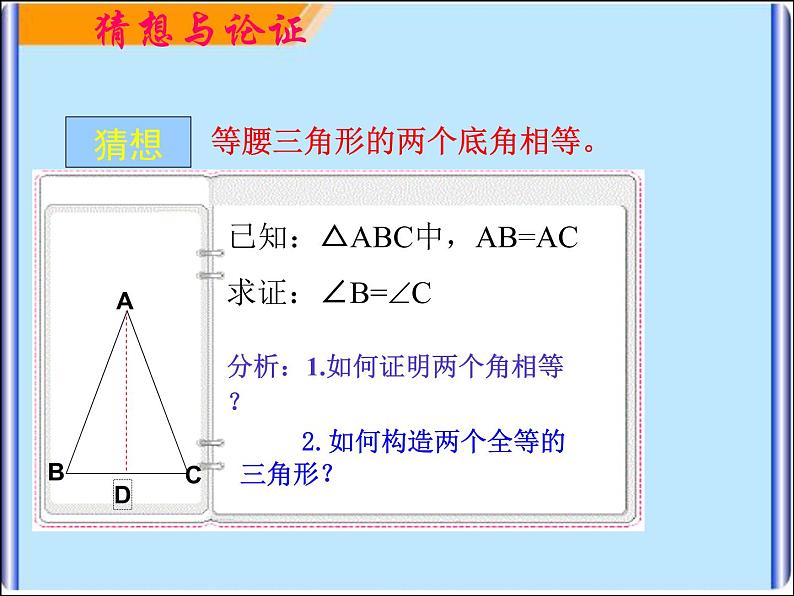
等腰三角形的两个底角相等。
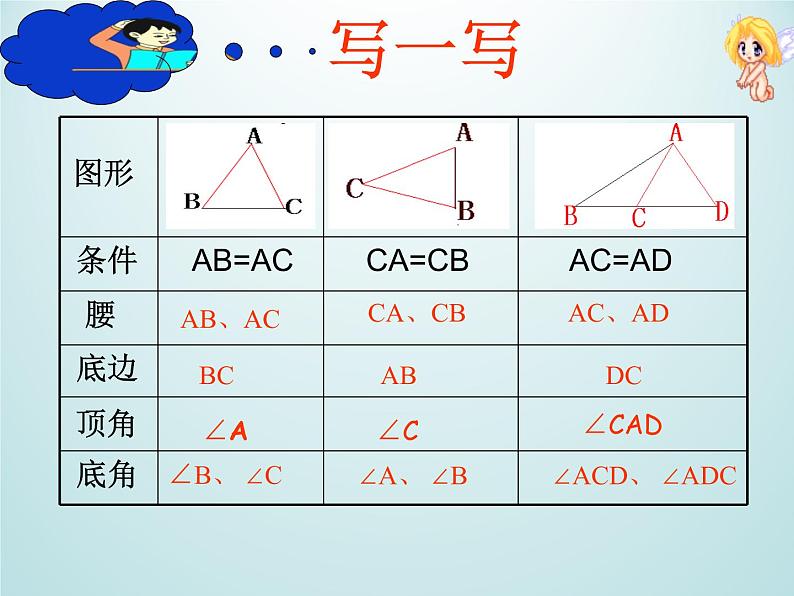
已知：△ABC中，AB=AC
分析：1.如何证明两个角相等？
　　2.如何构造两个全等的三角形？
已知： △ ABC中，AB=AC. 求证： ∠B= ∠C.
证明：等腰三角形的两个底角相等
作底边中线AD.则BD=CD 在△BAD和△CAD中，
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
作底边高线AD. 则∠ ADB= ∠ ADC=900 在Rt△BAD和△RtCAD中，
∴ Rt △BAD ≌ Rt △CAD (HL).
等腰三角形的性质１：
等腰三角形的两个底角相等 （简写成“等边对等角”）
注意：等边对等角是指 在 三角形中 。
在△ABC中， ∵ AB=AC ∴ ∠B=∠C ( ）
例1 （1）已知：在△ABC中，AB = AC，　并且其中一个角为80°，那么其它角的度数分别为_________________________. （2）已知：在△ABC中，AB = AC，　并且其中一个角为100°，那么其它角的度数分别为_______________________.
50°, 50°或80°, 20°
⒈等腰三角形一个底角为75°,它的另外两个 角为_____ __； ⒉等腰三角形一个角为70°,它的另外两个角 为___________________； ⒊等腰三角形一个角为110°,它的另外两个角 为______ __。
70°,40°或55°,55°
例2、如图，在△ABC中 ，AB=AC，点D在AC上，且 BD=BC=AD，求△ABC各角的度数。
例3：如图，在△ABC中， AB=AC，BD，CE 分别为∠ABC，∠ACB 的平分线。 求证：BD=CE.
根据等腰三角形性质2，在△ABC中，AB=AC时
　例 ：如图△ABC是一个屋顶的平面示意图，已知屋椽AB=AC，立柱AD⊥BC，底角∠B=40°，梁长BC=10米，则顶架上∠CAD=________度，BD=_____米.
△ABC中，AB＝AC，D是BC边上的中点， DF⊥AC于F DE ⊥ AB 于E .求证：DE＝DF。
证明： ∵DE⊥AB，DF⊥AC（已知）∴∠BED＝∠CFD 又∵D是BC中点（已知）∴BD＝DC ∵AB＝AC（已知） ∴∠B＝∠C（等边对等角）在△DBE与△DCF中 ∠DEB＝∠DFC（已证） ∠B＝∠C（已证）BD＝DC（已证） ∴ △BDE ≌ △CDF（AAS）∴DE＝DF
方法二：连AD 。 ∵AB＝AC，BD＝DC（已知） ∴AD是∠BAC的平分线。 （等腰三角形三线合一） 又∵DE⊥AB DF⊥AC ∴DE＝DF （角平分线上的点到这个 角的两边距离相等）
⒈等腰三角形一个底角为75°它的另外两个角为_____ ； ⒉等腰三角形一个顶角为70°它的另外两个角为_________；⒊等腰三角形一个角为80°, 它的另外两个角为 ______ __ 4、若等腰三角形的一个外角70°则它的底角为________
50°,50°或 80°,20°
1、在等腰△ABC中，AB =10，AC =12，则 △ABC的周长=32（ ）2、等腰三角形的两边分别是2和6，那么周长是10或14。（ ）3、等腰三角形的角平分线、中线和高互相重合。（ ）
1、如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警，当时测得∠A=∠B。 如果这两艘救生船以同样的速度同时出发，能不能大约同时赶到出事地点（不考虑风浪等因素）？
2.将一把三角尺和一个重锤如图放置，就能检查一根横梁是否水平，你知道怎么检查吗？
1.小红想做一个等腰三角形，于是她把一张长方形的纸沿对角线折叠，她说重合部分是一个等腰三角形，她说的对吗？为什么？
2.如图所示，已知下列两个三角形，思考 怎样把每个三角形只剪一次，将它分成两个 等腰三角形？试一试，你一定会成功的。
小结：通过本节课的学习你有收获吗？
1、本节主要教学知识是等腰三角形的两个性质。
等腰三角形的两个底角相等
等腰三角形的顶角 平分线、底边上的中线底边上的高互相重合。
∵AB＝AC（已知） ∴∠B＝∠C （等边对等角）
①∵AB＝AC，∠1＝∠2（已知） ∴BD＝DC，AD⊥BC（三线合一）② ∵AB＝AC，BD＝DC（已知） ∴ ∠1＝∠2， AD⊥BC（三线合一） ③∵ AB＝AC， AD⊥BC （已知） ∴ ∠1＝∠2， BD＝DC（三线合一）
2、本节课学习了数学思想及方法:分类讨论和一题多解。
1、课本P143 A组 1、3、4，B组1、2。2、用两种方法证明等腰三角形底角相等. （用符号语言说明）
一次数学课上，老师布置了一道几何证明题，通过大家的激烈讨论得到了许多种证明方法，聪明的你们，能找出几种证明方法呢？试试看吧！
如图，已知△ABC中，AB=AC,F在AC上，在BA的延长线上截取AE=AF,求证：ED⊥BC
已知：如图， △ ABC中， ∠ABC=50 º, ∠ACB=80 º,延长CB至D,使BD=BA,延长BC至E,使CE=CA .连结AD、AE.求∠D、∠E、∠DAE的度数 .
∵BD=CD∴∠D=∠DAB∵ ∠ABC=∠D+∠DAB∴∠D= ∠ABC=250
∵CE=CA∴∠E=∠CAE∵ ∠ACB=∠E+∠CAE∴∠E= ∠ACB=400
∵ ∠DAE+∠E+∠D=1800∴∠DAE= 1800-250-400=1150