

2021学年第十七章 特殊三角形17.1 等腰三角形教学ppt课件
展开1.了解等腰三角形的相关概念。2.探索并掌握等腰三角形的性质,会运用性质进行简单的推理、判断及计算。重点:等腰三角形性质及简单应用。难点:等腰三角形的“三线合一”的性质的理解及应用。
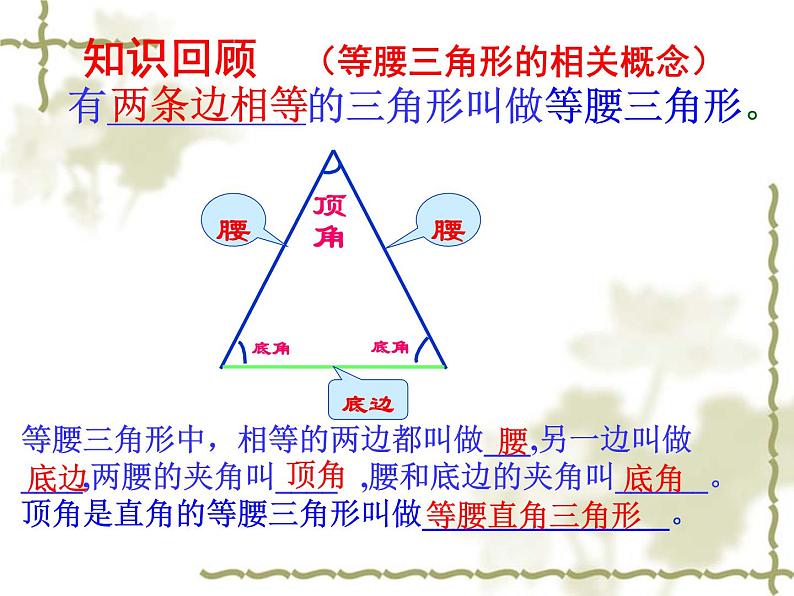
有__________的三角形叫做等腰三角形。
等腰三角形中,相等的两边都叫做___,另一边叫做 ____,两腰的夹角叫____ ,腰和底边的夹角叫______。顶角是直角的等腰三角形叫做________________。
知识回顾 (等腰三角形的相关概念)
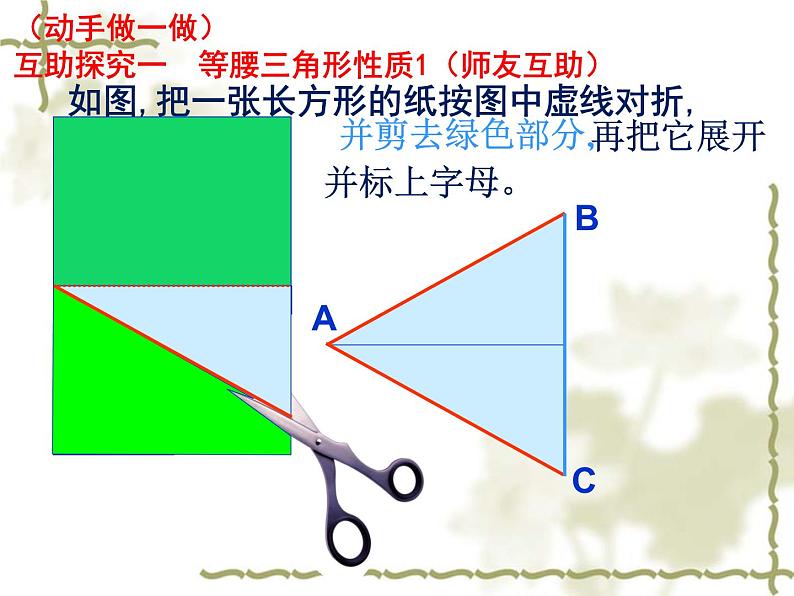
如图,把一张长方形的纸按图中虚线对折,
再把它展开并标上字母。
(动手做一做)互助探究一 等腰三角形性质1(师友互助)
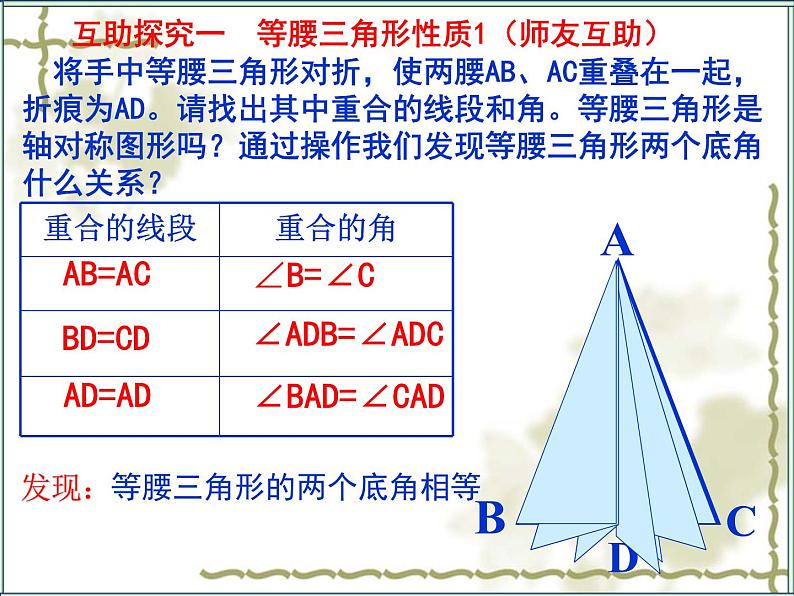
将手中等腰三角形对折,使两腰AB、AC重叠在一起,折痕为AD。请找出其中重合的线段和角。等腰三角形是轴对称图形吗?通过操作我们发现等腰三角形两个底角什么关系?
互助探究一 等腰三角形性质1(师友互助)
等腰三角形的两个底角相等
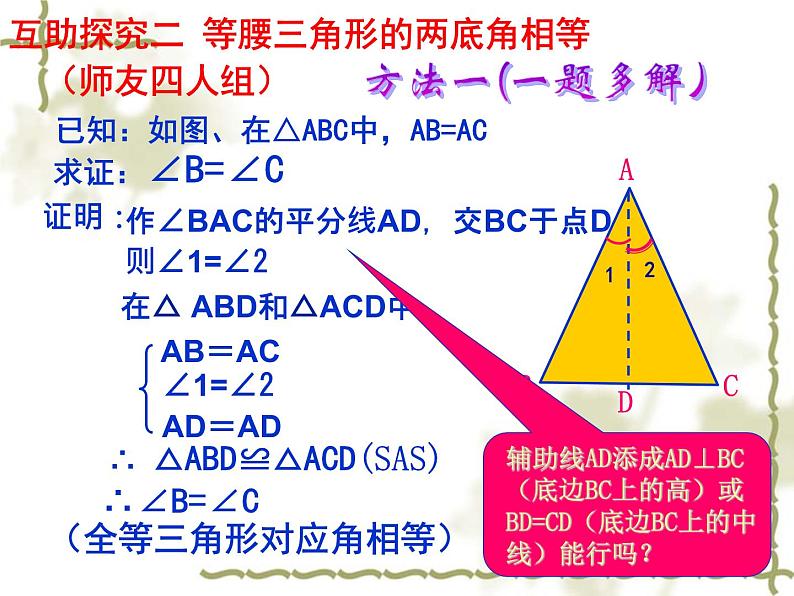
作∠BAC的平分线AD,交BC于点D,则∠1=∠2
在△ ABD和△ACD中
∴ △ABD≌△ACD(SAS) ∴∠B=∠C (全等三角形对应角相等)
辅助线AD添成AD⊥BC(底边BC上的高)或BD=CD(底边BC上的中线)能行吗?
互助探究二 等腰三角形的两底角相等 (师友四人组) 方法一(一题多解)
已知:如图、在△ABC中,AB=AC
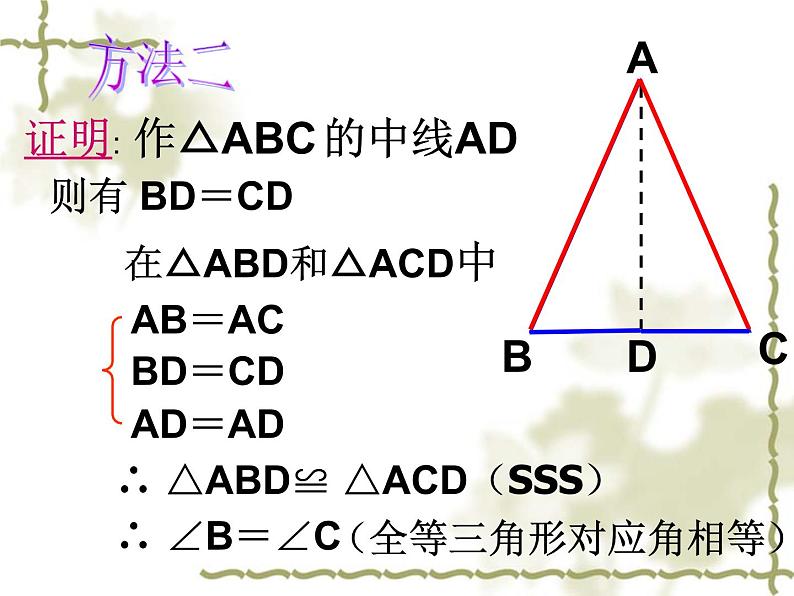
在△ABD和△ACD中
证明: 作△ABC 的中线AD
∴ △ABD≌ △ACD(SSS)
(全等三角形对应角相等)
证明: 作△ABC 的BC边上的高AD
用数学符号语言表示为:
在△ ABC中, ∵ AB=AC(已知)∴
注意:“边”和“角”必须在同一三角形中!
等腰三角形的两底角相等. (简称“等边对等角”)
归纳小结等腰三角形的性质1:
∠B=∠C (等边对等角)
1、等腰三角形一腰为4cm,底为3cm,则它的周长是 ;2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是 ;3、等腰三角形一个角为70°,它的另外两个角为: ___________________
10 cm 或 11 cm
70°,40°或55°,55°
跟踪训练一(师友互查)
互助探究三:等腰三角形性质2
∠ADB=∠ADC=90°
等腰三角形的顶角平分线、底边上的中线、底边上的高重合. (师友互助)
等腰三角形性质2 (师友互助)如图:已知AB=AC,AD是∠BAC的平分线求证:BD=CD, AD⊥BC
证明:∵AD是∠BAC的平分线 ∴∠1=∠2 在△ABD和△ACD中 AB=AC ∠1=∠2 AD=AD ∴ △ABD △ACD (SAS) ∴ BD=CD ∠BDA=∠ADC ∵∠BDA+∠ADC=180º ∴ ∠BDA=∠ADC=90º ∴ AD⊥BC
在△ABC中(1) ∵AB=AC,AD⊥BC, ∴∠__=∠__,____=____;(2) ∵AB=AC,AD是中线, ∴∠_=∠_,____⊥____; (3) ∵AB=AC,AD是角平分线, ∴____⊥____,____=____.
归纳性质2:等腰三角形的的顶角平分线、底边上的中线、底边上的高互相重合. (简称“三线合一)
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
如图,作△ABC的中线AD
如图, 作△ABC的高AD
如图,作顶角的角平分线AD
(1)等腰三角形的底角可能是锐角 或者直角、钝角都可以。( ) (2)等腰三角形的顶角平分线一定 垂直平分底边。 ( ) (3)等腰三角形的角平分线、中线 和高互相重合。 ( )
跟踪训练二:(学友大比拼)
2.如图,等腰三角形房屋钢架梁AB=AC,D是BC边上的中点,∠B=30。则∠1=_____∠ADC=_____
已知:如图,在△ABC中,AB=AC,BD,CE分别为∠ABC、∠ACB的平分线。 求证:BD=CE.
思考:等腰三角形两腰上的中线相等吗?高线相等吗?
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高重合,简称“三线合 一”
数学思想及方法:分类讨论、一题多解、利用等腰三角形的性质更容易证明:角相等、线段相等、垂直。
解决等腰三角形问题时常用的辅助线:作顶角的平分线、底边的高线、底边的中线
数学八年级上册17.1 等腰三角形教学ppt课件: 这是一份数学八年级上册17.1 等腰三角形教学ppt课件,共23页。PPT课件主要包含了建立数学模型,ABAC,你能验证你的结论吗,∠1∠2,∠B∠C,ADAD,∴ABAC,等腰三角形的判定方法,等角对等边,在△ABC中等内容,欢迎下载使用。
2020-2021学年17.1 等腰三角形多媒体教学课件ppt: 这是一份2020-2021学年17.1 等腰三角形多媒体教学课件ppt,共28页。PPT课件主要包含了ABAC,等腰三角形,AB与AC,BD与CD,AD与AD,∠B与∠C,∠BAD与∠CAD,∠ADB与∠ADC,求证∠BC,还有其他的证法吗等内容,欢迎下载使用。
数学八年级上册第十七章 特殊三角形17.1 等腰三角形教学ppt课件: 这是一份数学八年级上册第十七章 特殊三角形17.1 等腰三角形教学ppt课件,文件包含冀教版数学八年级上册171等腰三角形第2课时教学课件pptx、冀教版数学八年级上册171等腰三角形第2课时教案docx等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。













