北师大版九年级上册2 矩形的性质与判定图片ppt课件

这是一份北师大版九年级上册2 矩形的性质与判定图片ppt课件，共20页。PPT课件主要包含了情境导入，矩形性质，跟踪训练，矩形的相关概念及性质，轴对称图形，有两条对称轴，课堂小结等内容，欢迎下载使用。

2. 理解矩形与平行四边形的关系，正确运用矩形的性质解题．
3．在观察、操作、推理、归纳等探索过程中，发展学生的合情推理能力，进一步培养学生数学说理的习惯与能力.
1．探索并掌握矩形的概念及其特殊的性质.
1.矩形是平行四边形吗？
2.平行四边形经过怎样的变化就成为了矩形呢？
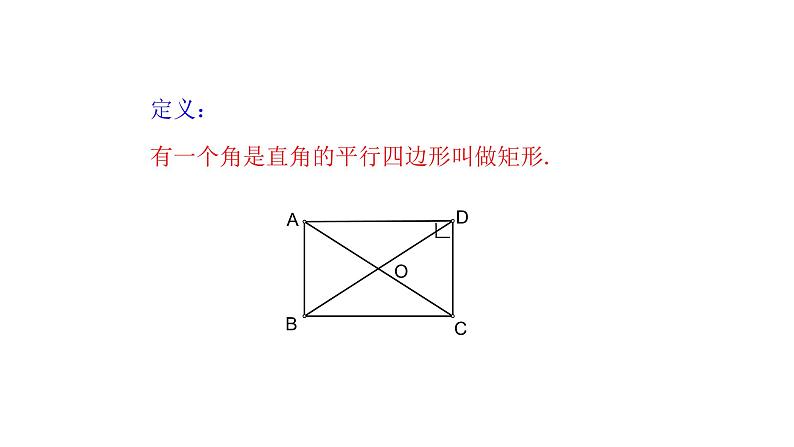
有一个角是直角的平行四边形叫做矩形.
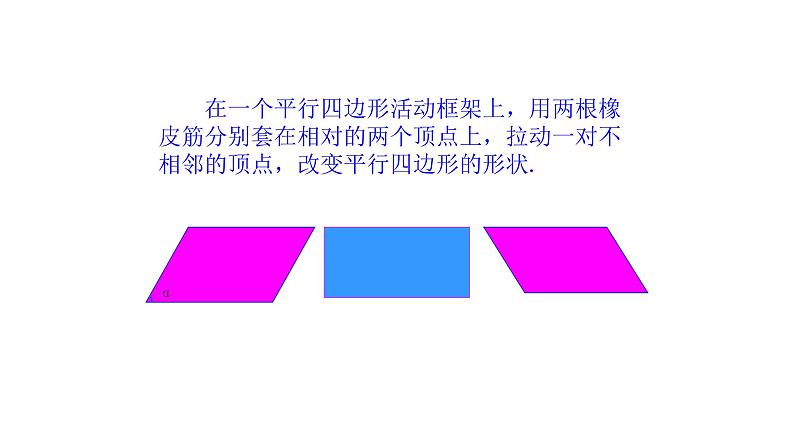
在一个平行四边形活动框架上，用两根橡皮筋分别套在相对的两个顶点上，拉动一对不相邻的顶点，改变平行四边形的形状.
(1)随着∠α的变化,两条对角线的长度怎样变化的？
(2)当∠α是锐角时，两条对角线的长度有什么关系？当∠α是钝角时呢？
(3)当∠α是直角时，平行四边形变成矩形，此时两条对角线的长度有什么关系？
解析：随着∠α的变化，一条对角线在变长，一条在变短.
解析：当∠α是锐角时，过∠α的顶点的那条对角线比另一条长;当∠α是钝角时，过∠α的顶点的那条对角线比另一条短.
解析：两条对角线相等.
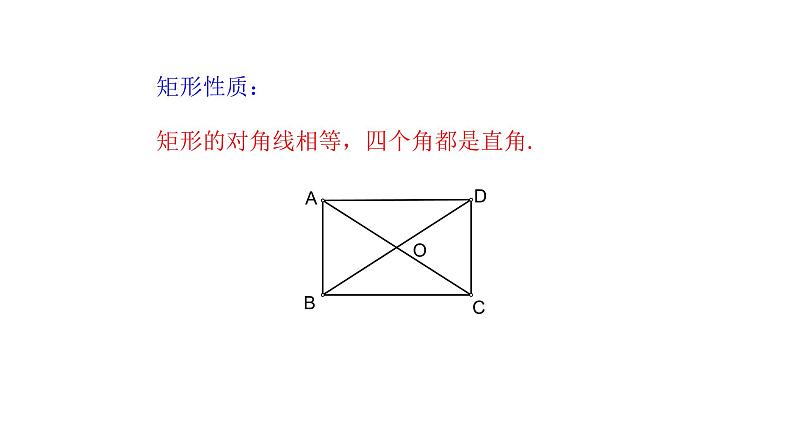
矩形的对角线相等，四个角都是直角.
【例题】如图：在矩形ABCD中，两条对角线AC,BD相交于点O, AB=OA=4cm.求BD与AD的长.
解：∵四边形ABCD是矩形,
∴BD=AC=2OA=8cm， ∠BAD＝90°.
在Rt△BAD中，根据勾股定理，得：
答：BD=8cm，AD= cm.
1.矩形是轴对称图形吗？如果是，它有几条对称轴？ 如果不是，简述你的理由.
矩形是轴对称图形，它有两条对称轴.
2.直角三角形斜边上的中线等于斜边长的一半，你能用矩形的有关性质解释这个结论吗？
【解析】在矩形ABCD中，
BO=OD，(矩形的对角线互相平分）BD=AC，（矩形的对角线相等）
具有平行四边形的一切性质
四个内角都是直角，两条对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫作矩形
1．（2021•成都期末）如图，在长方形ABCD中，AE平分∠BAD交BC于点E，连接ED，若ED＝5，EC＝3，则长方形的周长为（　　）A．20B．22C．24D．26
2.（2021•成都期末）下列性质中，菱形具有而矩形不一定具有的是（　　）A．对角线相等B．对角线垂直C．邻边垂直 D．邻角互补
3.（2021•济南期末）如图，矩形ABCD的两条对角线相交于点O，∠AOB＝60°，AO＝4，则AB的长是（　　）A．4B．5C．6D．8
4.（2021•北京模拟）已知矩形ABCD，一条直线将该矩形分割成两个多边形，则所得任一多边形的内角和度数不可能是（　　）A．180°B．360°C．540°D．720°
解析：不同的划分方法有4种，所得任一多边形内角和度数可能是360°或540°或180°．见图：
5.（2021•南京质检）利用矩形的性质，证明“直角三角形斜边上的中线等于斜边的一半”．已知：如图，　 　；求证：　 　；证明：
已知：Rt△ABC中，∠ACB＝90°，CO是斜边AB边上的中线；求证：CO＝ AB；证明：如图，延长CO至点E，使CO＝OE，连接AE,BE，∵CO＝OE，点O为AB中点，∴OA＝OC，∴四边形AEBC为平行四边形，∵∠ACB＝90°，∴平行四边形AEBC是矩形，∴CE＝AB，∵CO＝OE，∴CO＝ AB；
6.（2021•西安质检）如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，连接AE，若BE＝3，AF＝5，求AB的长．
解：∵EF是AC的垂直平分线，∴AO＝CO，∵四边形ABCD是矩形，∴AD∥BC，∴∠OAF＝∠OCE，