2021学年5.4 三角函数的图象与性质示范课ppt课件

这是一份2021学年5.4 三角函数的图象与性质示范课ppt课件，共26页。PPT课件主要包含了课程目标，数学学科素养，自主预习回答问题，知识清单，小试牛刀等内容，欢迎下载使用。
1.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法，能用“五点法”作出简单的正弦、余弦曲线.2.理解正弦曲线与余弦曲线之间的联系.
1.数学抽象：正弦曲线与余弦曲线的概念；2.逻辑推理：正弦曲线与余弦曲线的联系；3.直观想象：正弦函数余弦函数的图像；4.数学运算：五点作图；5.数学建模：通过正弦、余弦图象图像，解决不等式问题及零点问题，这正是数形结合思想方法的应用.
阅读课本196-199页，思考并完成以下问题1.任意角的正弦函数在单位圆中是怎样定义的？2．怎样作出正弦函数y=sinx的图像？3.怎样作出余弦函数 的图像？4.正弦曲线与余弦曲线的区别与联系. 要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。
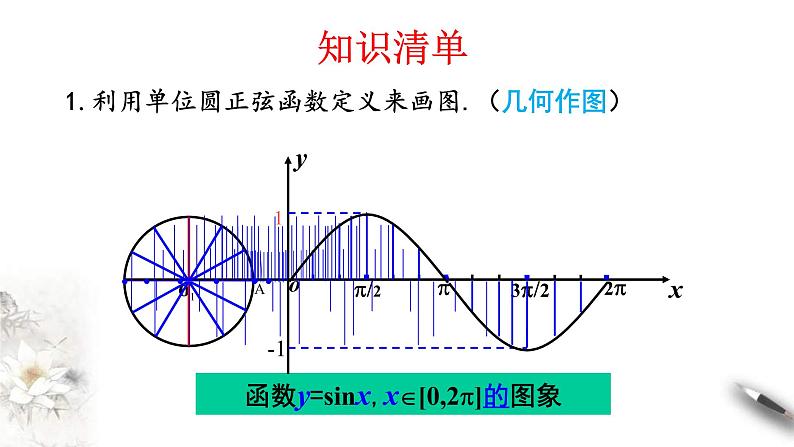
函数y=sinx,x[0,2]的图象
1.利用单位圆正弦函数定义来画图.（几何作图）
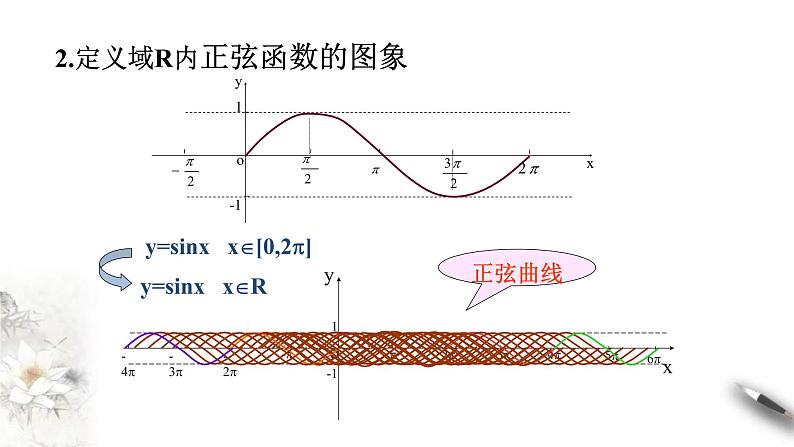
2.定义域R内正弦函数的图象
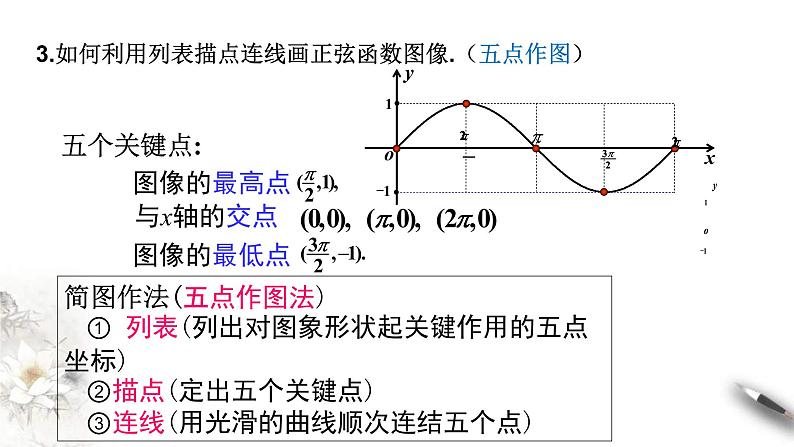
简图作法(五点作图法) ① 列表(列出对图象形状起关键作用的五点坐标) ②描点(定出五个关键点) ③连线(用光滑的曲线顺次连结五个点)
3.如何利用列表描点连线画正弦函数图像.（五点作图）
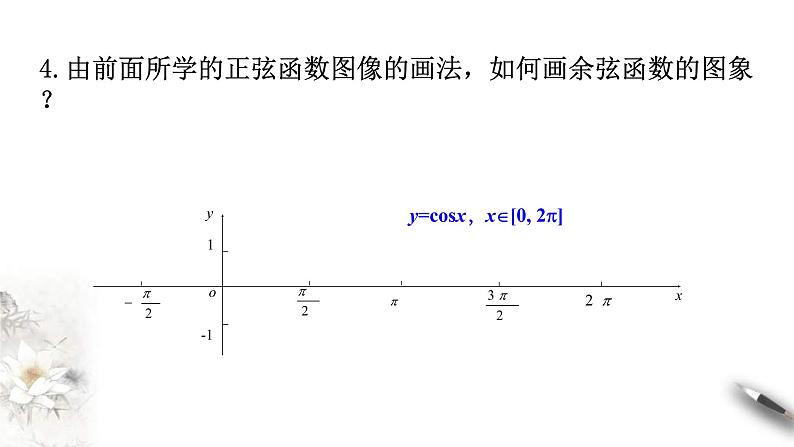
4.由前面所学的正弦函数图像的画法，如何画余弦函数的图象？
y=csx，x[0, 2]
找出余弦函数y= csx，x[0, 2]图象五个关键点：
方法总结： 在精确度要求不高时，先作出函数y=sinx和y= csx的五个关键点，再用平滑的曲线将它们顺次连结起来，就得到函数的简图。这种作图法叫做“五点（画图）法”。
5.正弦、余弦函数的图象关系
余弦函数的图象
正弦函数的图象
y=csx=sin(x+ ), xR
形状完全一样只是位置不同
解析：　由y＝sin x在[0,2π]上的图象作关于x轴的对称图形，应为D项.
2.下列图象中，是y＝－sin x在[0,2π]上的图象的是(　　)
例1 （1） 用“五点作图法”画出函数y=1+sinx，x[0, 2]的简图：
1 2 1 0 1
y=1+sinx，x[0, 2]
步骤：1.列表2.描点3.连线
题型分析 举一反三
题型一 作正弦函数、余弦函数的简图
例1（2）用“五点作图法” 画出函数y= - csx，x[0, 2]的简图：
-1 0 1 0 -1
y=sinx，x[0, 2]
总结：函数值加减，图像上下移动
延伸探究1：如何利用y=sinx，x[0, 2]的图象，得到y=1+sinx，x[0, 2]的图象？
总结：这两个图像关于X轴对称。
延伸探究2如何利用y= csx，x[0, 2]的图象，得到y= -csx，x[0, 2]的图象？
y= - csx，x[0, 2]
y= csx，x[0, 2]
解题方法（简单三角函数图像画法）
1、五点作图法：作正弦曲线、余弦曲线要理解几何法作图，掌握五点法作图.“五点”即y＝sin x或y＝cs x的图象在[0,2π]内的最高点、最低点和与x轴的交点.2、图象变换：平移变换、对称变换、翻折变换.
0 1 0 1 0
1.（1）用“五点作图法”画出函数y= |sinx| ，x[0, 2]的简图：
1.（2）利用正弦函数图象变换作出下列函数的简图：y＝|sinx|，x∈[0,4π]．
首先用五点法作出函数y＝sinx，x∈[0,4π]的图象，再将x轴下方的部分对称到x轴的上方．如图(2)所示．
总结：关于X轴翻折变换。
2. 在给定的直角坐标系如图4中，作出函数在区间[0，π]上的图象．
描点连线作出函数 在区间[0，π]上的图象如图5所示
题型二 正弦函数、余弦函数图象的简单应用
结合图象可得：x∈[－4，－π)∪(0，π).
解析：建立平面直角坐标系xOy，先用五点法画出函数y＝sin x，x∈[0,2π]的图象，再依次向左、右连续平移2π个单位，得到y＝sin x的图象.描出点(1,0)，(10,1)，并用光滑曲线连接得到y＝lg x的图象，如图所示.
例3　在同一坐标系中，作函数y＝sin x和y＝lg x的图象，根据图象判断出方程sin x＝lg x的解的个数.
由图象可知方程sin x＝lg x的解有3个.
解题方法（正弦函数、余弦函数图象的简单应用）
1.解不等式问题：三角函数的定义域或不等式可以借助函数图象直观地观察得到，同时要注意区间端点的取舍.2.方程的根(或函数零点)问题：三角函数的图象是研究函数的重要工具，通过图象可较简便的解决问题，这正是数形结合思想方法的应用.
解析：　由题意知，自变量x应满足2sin x－1≥0，