

2020-2021学年江苏省扬州市七年级(下)期中数学试卷 解析版
展开2020-2021学年江苏省扬州市七年级(下)期中数学试卷
一、选择题(本大题共8小题,每小题3分,共计24分)
1.(3分)如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.7
2.(3分)世界上最小的开花结果植物是出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076g,将数0.000000076用科学记数法表示为( )
A.0.76×10﹣7 B.7.6×10﹣8 C.7.6×10﹣9 D.76×10﹣10
3.(3分)下列长度的三条线段能组成三角形的是( )
A.1cm,2cm,3.5cm B.4cm,5cm,9cm
C.5cm,8cm,15cm D.6cm,8cm,9cm
4.(3分)计算0.256×(﹣32)2等于( )
A.﹣ B. C.1 D.﹣1
5.(3分)如图所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2 C.∠3=∠4 D.∠BAC=∠ACD
6.(3分)若(x+a)(x+b)=x2﹣kx+ab,则k的值为( )
A.a+b B.﹣a﹣b C.a﹣b D.b﹣a
7.(3分)若a2+b2=2,a+b=1,则ab的值为( )
A.﹣1 B.﹣ C. D.3
8.(3分)若a+2b﹣3c=3,5a﹣6b+7c=5,则a﹣6b+8c的值是( )
A.﹣2 B.2 C.0 D.﹣1
二、填空题(本大题共10小题,每小题3分,共30分)
9.(3分)一个n边形的内角和比外角和多180°,则n= .
10.(3分)定义一种运算☆,其规则为a☆b=+,根据这个规则,计算2☆3的值是 .
11.(3分)若实数x、y满足方程组,则代数式2x+3y﹣4的值是 .
12.(3分)若a2+a+1=2,则(5﹣a)(6+a)= .
13.(3分)若(2﹣3x)(ax+1)的乘积中不含x的一次项,则a= .
14.(3分)已知a,b,c是△ABC的三边长,b,c满足(b﹣2)2+|c﹣3|=0,且a为方程|x﹣4|=2的解,则△ABC的周长= .
15.(3分)已知x2﹣3x+1=0,则x4+= .
16.(3分)规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.则:(2,)= .
17.(3分)如图,在平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线,若AE=3,BE=2,则平行四边形ABCD的面积为 .
18.(3分)如图,已知AB∥CD,∠ABE的平分线与∠CDE的平分线相交于点F.当∠ABM=∠ABF,∠CDM=∠CDF时,请你写出∠M与∠E之间的关系 .
三、解答题(本大题共10小题,共96分)
19.(8分)计算:
(1)20092﹣2010×2008;
(2)(x﹣y)(4x+3y)﹣(2x+y)(2x﹣y).
20.(8分)分解因式:
(1)3ab3﹣30a2b2+75a3b;
(2)a2(x﹣y)+16(y﹣x).
21.(8分)(1)
(2)
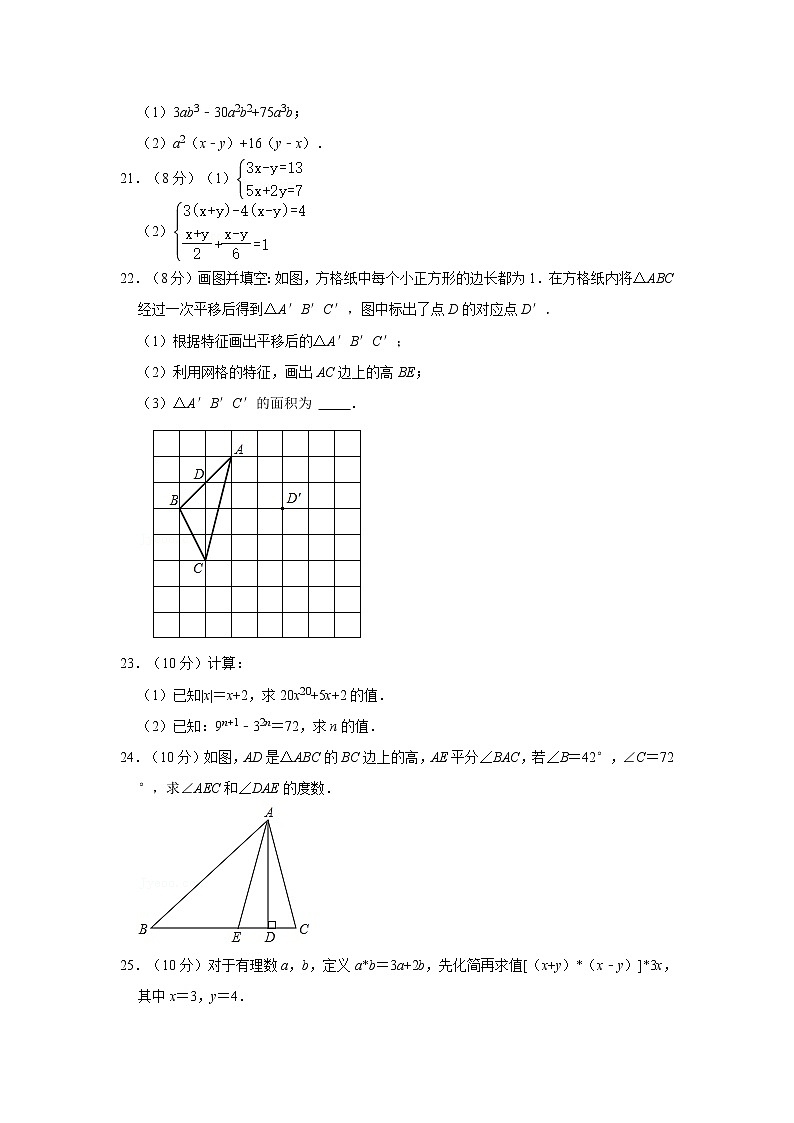
22.(8分)画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE;
(3)△A′B′C′的面积为 .
23.(10分)计算:
(1)已知|x|=x+2,求20x20+5x+2的值.
(2)已知:9n+1﹣32n=72,求n的值.
24.(10分)如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=72°,求∠AEC和∠DAE的度数.
25.(10分)对于有理数a,b,定义a*b=3a+2b,先化简再求值[(x+y)*(x﹣y)]*3x,其中x=3,y=4.
26.(10分)先阅读,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0,
∴m2+2mn+n2+n2﹣6n+9=0,
∴(m+n)2+(n﹣3)2=0,
∴m+n=0,n﹣3=0,
∴n=3,m=﹣3.
问题:
(1)若x2+2y2﹣2xy+4y+4=0,求xy的值;
(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0,请问△ABC是怎样形状的三角形?
(3)根据以上的方法是说明代数式:2x2+8x+y2﹣8y+25的值一定是一个正数.
27.(12分)数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)请写出图1,图2,图3阴影部分的面积分别能解释的乘法公式.
图1 ,
图2 ,
图3 .
(2)用4个全等的长和宽分别为a,b的长方形拼摆成一个如图4的正方形,请你通过计算阴影部分的面积,写出这三个代数式(a+b)2,(a﹣b)2,ab之间的等量关系.
(3)根据(2)中你探索发现的结论,计算:当x+y=2,xy=﹣8时,求x﹣y的值.
28.(12分)(1)如图1,AB∥CD,点E是在AB、CD之间,且在BD的左侧平面区域内一点,连接BE、DE.求证:∠E=∠ABE+∠CDE.
(2)如图2,在(1)的条件下,作出∠EBD和∠EDB的平分线,两线交于点F,猜想∠F、∠ABE、∠CDE之间的关系,并证明你的猜想.
(3)如图3.AB∥EF,∠E=90°,求∠α,∠β,∠γ之间的关系.
2020-2021学年江苏省扬州市七年级(下)期中数学试卷
参考答案与试题解析
一、选择题(本大题共8小题,每小题3分,共计24分)
1.(3分)如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.7
【分析】观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE=5﹣3=2,进而可得答案.
【解答】解:根据平移的性质,
易得平移的距离=BE=5﹣3=2,
故选:A.
2.(3分)世界上最小的开花结果植物是出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076g,将数0.000000076用科学记数法表示为( )
A.0.76×10﹣7 B.7.6×10﹣8 C.7.6×10﹣9 D.76×10﹣10
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.000 0000 76=7.6×10﹣8,
故选:B.
3.(3分)下列长度的三条线段能组成三角形的是( )
A.1cm,2cm,3.5cm B.4cm,5cm,9cm
C.5cm,8cm,15cm D.6cm,8cm,9cm
【分析】根据三角形的三边关系对各选项进行逐一判断即可.
【解答】解:A、∵1+2=3<3.5,∴不能构成三角形,故本选项错误;
B、∵4+5=9,∴不能构成三角形,故本选项错误;
C、∵8<15﹣5=10,∴不能构成三角形,故本选项错误;
D、∵9﹣6<8<9+6,∴能构成三角形,故本选项正确.
故选:D.
4.(3分)计算0.256×(﹣32)2等于( )
A.﹣ B. C.1 D.﹣1
【分析】逆用幂的乘方的公式,把0.256转化为指数是2的形式,再逆用积的乘方的公式即可.
【解答】解:原式=[()3]2×322
=(×32)2
=()2
=,
故选:B.
5.(3分)如图所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2 C.∠3=∠4 D.∠BAC=∠ACD
【分析】A、由于∠BAD=∠BCD,而这两个角是对角关系,不是内错角、同位角、同旁内角的关系,故不能判定AB∥CD;
B、由∠1=∠2,可证AD∥BC;
C、由∠3=∠4,可证AD∥BC;
D、由∠BAC=∠ACD,可证AB∥CD.
【解答】解:A、∵∠BAD=∠BCD,
而这两个角是对角关系,不是内错角、同位角、同旁内角的关系,
∴不能判定AB∥CD,
故此选项错误;
B、∵∠1=∠2,
∴AD∥BC,
故此选项错误;
C、∵∠3=∠4,
∴AD∥BC,
故此选项错误;
D、∵∠BAC=∠ACD,
∴AB∥CD,
故此选项正确.
故选:D.
6.(3分)若(x+a)(x+b)=x2﹣kx+ab,则k的值为( )
A.a+b B.﹣a﹣b C.a﹣b D.b﹣a
【分析】已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件即可求出k.
【解答】解:(x+a)(x+b)=x2+(a+b)x+ab=x2﹣kx+ab,
得到a+b=﹣k,
则k=﹣a﹣b.
故选:B.
7.(3分)若a2+b2=2,a+b=1,则ab的值为( )
A.﹣1 B.﹣ C. D.3
【分析】将a+b=1两边平方,利用完全平方公式展开,把a2+b2=2代入计算即可求出ab的值.
【解答】解:将a+b=1两边平方得:(a+b)2=a2+b2+2ab=1,
将a2+b2=2代入得:2+2ab=1,
解得:ab=﹣.
故选:B.
8.(3分)若a+2b﹣3c=3,5a﹣6b+7c=5,则a﹣6b+8c的值是( )
A.﹣2 B.2 C.0 D.﹣1
【分析】先把方程a+2b﹣3c=3的左右两边同乘以3得到3a+6b﹣9c=9,然后再同方程5a﹣6b+7c=5相减即可得到答案.
【解答】解:∵a+2b﹣3c=3,
∴3a+6b﹣9c=9①,
又∵5a﹣6b+7c=5②,
∴②﹣①得:2a﹣12b+16c=﹣4.
∴a﹣6b+8c=﹣2,
故选:A.
二、填空题(本大题共10小题,每小题3分,共30分)
9.(3分)一个n边形的内角和比外角和多180°,则n= 5 .
【分析】根据多边形的内角和公式(n﹣2)•180°,外角和等于360°列出方程求解即可.
【解答】解:设多边形的边数是n,
根据题意得,(n﹣2)•180°﹣360°=180°,
解得n=5.
故答案为:5.
10.(3分)定义一种运算☆,其规则为a☆b=+,根据这个规则,计算2☆3的值是 .
【分析】根据a☆b=+,则2☆3=+,然后通分后相加即可.
【解答】解:2☆3=+=.
故答案为.
11.(3分)若实数x、y满足方程组,则代数式2x+3y﹣4的值是 2 .
【分析】方程组两方程左右两边相加求出2x+3y的值,代入原式计算即可得到结果.
【解答】解:,
①+②得:4x+6y=12,即2x+3y=6,
则原式=6﹣4=2,
故答案为:2
12.(3分)若a2+a+1=2,则(5﹣a)(6+a)= 29 .
【分析】根据题意先求出a2+a的值,再根据多项式乘以多项式的法则求出要求的式子,然后代入计算即可.
【解答】解:∵a2+a+1=2,
∴a2+a=1,
∴(5﹣a)(6+a)=30﹣a﹣a2=30﹣(a2+a)=30﹣1=29;
故答案为:29.
13.(3分)若(2﹣3x)(ax+1)的乘积中不含x的一次项,则a= .
【分析】首先利用多项式乘多项式的计算方法进行乘法运算,再根据乘积中不含x的一次项,使含x的一次项的系数之和等于0即可.
【解答】解:(2﹣3x)(ax+1)
=﹣3ax2+2ax﹣3x+2
=﹣3ax2+(2a﹣3)x+2,
∵乘积中不含x的一次项,
∴2a﹣3=0,
解得:a=,
故答案为:.
14.(3分)已知a,b,c是△ABC的三边长,b,c满足(b﹣2)2+|c﹣3|=0,且a为方程|x﹣4|=2的解,则△ABC的周长= 7 .
【分析】利用绝对值的性质以及偶次方的性质得出b,c的值,进而利用三角形三边关系得出a的值,进而求出△ABC的周长.
【解答】解:∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0且c﹣3=0,
∴b=2、c=3,
∵a为方程|x﹣4|=2的解,
∴a=2或a=6,
又c﹣b<a<c+b,即1<a<5,
∴a=2,
则△ABC的周长为2+2+3=7,
故答案为:7.
15.(3分)已知x2﹣3x+1=0,则x4+= 47 .
【分析】将方程x2﹣3x+1=0两边同除以x,即可得到x+的值,然后完全平方得到x2+的值,再完全平方即可得到所求式子的值.
【解答】解:∵x2﹣3x+1=0,
∴x﹣3+=0,
∴x+=3,
∴(x+)2=9,
∴x2+=7,
∴(x2+)2=49,
∴x4+==47,
故答案为:47.
16.(3分)规定两数a,b之间的一种运算,记作(a,b):如果ac=b,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.则:(2,)= ﹣2 .
【分析】根据新定义的运算和表示方法求解即可.
【解答】解:∵,
∴(2,)=﹣2;
故答案为:﹣2.
17.(3分)如图,在平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线,若AE=3,BE=2,则平行四边形ABCD的面积为 6 .
【分析】利用角平分线的性质结合平行四边形的性质得出∠EAB+∠EBA=90°,进而利用直角三角形的性质求出答案.
【解答】解:∵AE是∠DAB的平分线,BE是∠CBA的平分线,
∴∠DAE=∠EAB,∠CBE=∠ABE,
∵AD∥BC,
∴∠DAB+∠CBA=180°,
∴∠EAB+∠EBA=90°,
∵AE=3,BE=2,
∴S△ABE=×2×3=3,
∴平行四边形ABCD的面积=2×3=6,
故答案为6.
18.(3分)如图,已知AB∥CD,∠ABE的平分线与∠CDE的平分线相交于点F.当∠ABM=∠ABF,∠CDM=∠CDF时,请你写出∠M与∠E之间的关系 6∠BMD+∠BED=360°. .
【分析】首先作EG∥AB,MH∥AB,利用平行线的性质可得∠ABE+∠CDE+∠BED=360°,∠BMD=∠ABM+∠CDM,再利用角平分线的定义及已知条件得到∠ABE=6∠ABM,∠CDE=6∠CDM,最后得出6∠BMD+∠BED=360°即可得解.
【解答】解:过点E作EN∥AB,过点M作MH∥AB,
∵AB∥CD,
∴EN∥CD,MH∥CD,
∴∠ABE+∠BEN=180°,∠CDE+∠DEN=180°,
∴∠ABE+∠BEN+∠CDE+∠DEN=360°,
即∠ABE+∠BED+∠CDE=360°,
∵∠ABM=∠ABF,∠CDM=∠CDF,
∴∠ABF=3∠ABM,∠CDF=3∠CDM,
∵∠ABE与∠CDE两个角的角平分线相交于点F,
∴∠ABE=6∠ABM,∠CDE=6∠CDM,
∴6∠ABM+6∠CDM+∠BED=360°,
∵MH∥AB,MH∥CD,
∴∠ABM=∠BMH,∠CDM=∠DMH,
∴∠BMD=∠BMH+∠DMH=∠ABM+∠CDM,
∴6∠BMD+∠BED=360°,
故答案为:6∠BMD+∠BED=360°.
三、解答题(本大题共10小题,共96分)
19.(8分)计算:
(1)20092﹣2010×2008;
(2)(x﹣y)(4x+3y)﹣(2x+y)(2x﹣y).
【分析】(1)根据平方差公式进行计算即可;
(2)根据多项式乘多项式的运算法则、平方差公式进行计算即可.
【解答】解:(1)原式=20092﹣(2009+1)×(2009﹣1)
=20092﹣20092+1
=1;
(2)原式=4x2+3xy﹣4xy﹣3y2﹣(4x2﹣y2)
=4x2+3xy﹣4xy﹣3y2﹣4x2+y2
=﹣2y2﹣xy.
20.(8分)分解因式:
(1)3ab3﹣30a2b2+75a3b;
(2)a2(x﹣y)+16(y﹣x).
【分析】(1)直接提取公因式3ab,再利用完全平方公式分解因式得出答案;
(2)直接将原式变形,提取公因式(x﹣y),再利用平方差公式分解因式进而得出答案.
【解答】解:(1)3ab3﹣30a2b2+75a3b
=3ab(b2﹣10ab+25a2)
=3ab(b﹣5a)2;
(2)原式=a2(x﹣y)﹣16(x﹣y)
=(x﹣y)(a2﹣16)
=(x﹣y)(a+4)(a﹣4).
21.(8分)(1)
(2)
【分析】(1)应用代入消元法,求出方程组的解是多少即可.
(2)应用加减消元法,求出方程组的解是多少即可.
【解答】解:(1),
由①,可得:y=3x﹣13③,
③代入②,可得:5x+2(3x﹣13)=7,
解得x=3,
把x=3代入③,解得y=﹣4,
∴原方程组的解是.
(2)由,
可得:,
①×2﹣②×7,可得﹣30x=﹣34,
解得x=,
把x=代入①,解得y=,
∴原方程组的解是.
22.(8分)画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE;
(3)△A′B′C′的面积为 3 .
【分析】(1)利用平移变换的性质分别作出A,B,C的对应点A′,B′,C′即可.
(2)根据三角形的高的定义作出图形即可.
(3)利用分割法把三角形面积看成矩形面积减去周围三个三角形面积即可.
【解答】解:(1)如图,△A′B′C′即为所求.
(2)如图,线段BE即为所求.
(3)△A′B′C′的面积=2×4﹣×2×2﹣×1×2﹣×1×4=3,
故答案为:3.
23.(10分)计算:
(1)已知|x|=x+2,求20x20+5x+2的值.
(2)已知:9n+1﹣32n=72,求n的值.
【分析】(1)根据绝对值的性质求出x的值,再代入所求式子计算即可;
(2)根据72=9×8,而9n+1﹣32n=9n×8,得出9n=9,从而得出n的值.
【解答】解:(1)∵|x|=x+2,
∴x<0,
∴﹣x=x+2,
解得x=﹣1,
∴原式=20×1﹣5+2=17;
(2):∵9n+1﹣32n=9n+1﹣9n=9n(9﹣1)=9n×8,而72=9×8,
∴当9n+1﹣32n=72时,9n×8=9×8,
∴9n=9,
∴n=1.
24.(10分)如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=72°,求∠AEC和∠DAE的度数.
【分析】根据三角形内角和定理求出∠BAC,根据角平分线的定义得到∠BAE=∠CAE=∠BAC=33°,根据三角形的外角性质求出∠AEC,根据直角三角形的性质求出∠DAE.
【解答】解:∵∠BAC+∠B+∠C=180°,∠B=42°,∠C=72°,
∴∠BAC=66°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=33°,
∴∠AEC=∠B+∠BAE=75°,
∵AD⊥BC,
∴∠ADE=90°,
∴∠DAE=90°﹣∠AEC=15°.
25.(10分)对于有理数a,b,定义a*b=3a+2b,先化简再求值[(x+y)*(x﹣y)]*3x,其中x=3,y=4.
【分析】直接利用新定义将原式变形,利用整式的加减运算法则计算,进而代入已知数据得出答案.
【解答】解:[(x+y)*(x﹣y)]*3x
=[3(x+y)+2(x﹣y)]*3x
=(3x+3y+2x﹣2y)*3x
=(5x+y)*3x
=3(5x+y)+2•3x
=15x+3y+6x
=21x+3y,
当x=3,y=4时,
原式=21×3+3×4=75.
26.(10分)先阅读,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0,
∴m2+2mn+n2+n2﹣6n+9=0,
∴(m+n)2+(n﹣3)2=0,
∴m+n=0,n﹣3=0,
∴n=3,m=﹣3.
问题:
(1)若x2+2y2﹣2xy+4y+4=0,求xy的值;
(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0,请问△ABC是怎样形状的三角形?
(3)根据以上的方法是说明代数式:2x2+8x+y2﹣8y+25的值一定是一个正数.
【分析】(1)将原式配方得(x﹣y)2+(y+2)2=0,求出x,y的值,进而求解.
(2)将原式配方得(a﹣3)2+(b﹣3)2+|3﹣c|=0,求出a,b,c的值进而求解.
(3)将原式配方得2(x+2)2+(y﹣4)2+1,由偶次方及绝对值的非负性求解.
【解答】解:(1)x2+2y2﹣2xy+4y+4=x2﹣2xy+y2+y2+4y+4=(x﹣y)2+(y+2)2=0,
∴x﹣y=0,y+2=0,
∴x=y=﹣2,
∴xy=(﹣2)﹣2=.
(2)a2+b2﹣6a﹣6b+18+|3﹣c|=(a﹣3)2+(b﹣3)2+|3﹣c|=0,
∴a=b=c=3,
∴△ABC是等边三角形.
(3)2x2+8x+y2﹣8y+25=2(x2+4x+4)+y2﹣8y+16+1=2(x+2)2+(y﹣4)2+1,
∴2(x+2)2+(y﹣4)2+1≥1,
∴原式的值一定为正数.
27.(12分)数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)请写出图1,图2,图3阴影部分的面积分别能解释的乘法公式.
图1 (a+b)2=a2+2ab+b2 ,
图2 (a﹣b)2=a2﹣2ab+b2 ,
图3 (a+b)(a﹣b)=a2﹣b2 .
(2)用4个全等的长和宽分别为a,b的长方形拼摆成一个如图4的正方形,请你通过计算阴影部分的面积,写出这三个代数式(a+b)2,(a﹣b)2,ab之间的等量关系.
(3)根据(2)中你探索发现的结论,计算:当x+y=2,xy=﹣8时,求x﹣y的值.
【分析】(1)根据两种方法计算的阴影部分面积相等直接得出即可;
(2)用两种方法表示阴影部分的面积可得结论;
(3)根据(2)中公式,整体代入求解即可.
【解答】解:(1)图1:(a+b)2=a2+2ab+b2,
图2:(a﹣b)2=a2﹣2ab+b2,
图3:(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,(a+b)(a﹣b)=a2﹣b2;
(2)∵阴影部分是一个正方形,边长为(a﹣b),
∴阴影部分面积为(a﹣b)2,
∵阴影部分的面积等于大正方形的面积减去4个小长方形的面积,
∴阴影部分的面积为(a+b)2﹣4ab,
∴(a﹣b)2=(a+b)2﹣4ab;
(3)∵(x﹣y)2=(x+y)2﹣4xy=22﹣4×(﹣8)=4+32=36,
∴x﹣y=±6.
28.(12分)(1)如图1,AB∥CD,点E是在AB、CD之间,且在BD的左侧平面区域内一点,连接BE、DE.求证:∠E=∠ABE+∠CDE.
(2)如图2,在(1)的条件下,作出∠EBD和∠EDB的平分线,两线交于点F,猜想∠F、∠ABE、∠CDE之间的关系,并证明你的猜想.
(3)如图3.AB∥EF,∠E=90°,求∠α,∠β,∠γ之间的关系.
【分析】(1)利用平行线的性质即可得出结论;
(2)先判断出∠EBD+∠EDB=180°﹣(∠ABE+∠CDE),进而得出∠DBF+∠BDF=90°﹣(∠ABE+∠CDE),最后用三角形的内角和即可得出结论;
(3)将线段EF向两方延长,分别交AB、CD于点M、N,即可根据三角形内角和、三角形的外角性质及平行线的性质得解.
【解答】(1)证明:如图1,过点E作EH∥AB,
∴∠BEH=∠ABE,
∵EH∥AB,CD∥AB,
∴EH∥CD,
∴∠DEH=∠CDE,
∴∠BED=∠BEH+∠DEH=∠ABE+∠CDE;
(2)解:2∠F﹣(∠ABE+∠CDE)=180°,理由如下:
由(1)知:∠BED=∠ABE+∠CDE,
∵∠EDB+∠EBD+∠BED=180°,
∴∠EDB+∠EBD=180°﹣∠BED=180°﹣(∠ABE+∠CDE),
∵BE、DF分别是∠EBD和∠EDB的平分线,
∴∠EBD=2∠DBF,∠EDB=2∠BDF,
∴2∠DBF+2∠BDF=180°﹣(∠ABE+∠CDE),
∴∠DBF+∠BDF=90°﹣(∠ABE+∠CDE),
在△BDF中,
∠F=180°﹣(∠DBF+∠BDF)
=180°﹣[90°﹣(∠ABE+∠CDE)]
=90°+(∠ABE+∠CDE)
即2∠F﹣(∠ABE+∠CDE)=180°.
(3)解:∠α+∠β﹣∠γ=90°,理由如下:
如图3,将线段EF向两方延长,分别交AB、CD于点M、N,
则∠BMN=90°﹣∠α,∠MNC=∠β﹣∠γ,
∵AB∥EF,
∴∠BMN=∠MNE,
∴90°﹣∠α=∠β﹣∠γ,
即:∠α+∠β﹣∠γ=90°.
2022-2023学年江苏省扬州市梅岭中学教育集团七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年江苏省扬州市梅岭中学教育集团七年级(下)期中数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年江苏省扬州市仪征市七年级(下)期中数学试卷(含解析): 这是一份2022-2023学年江苏省扬州市仪征市七年级(下)期中数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2017-2018学年江苏省扬州市邗江区梅岭中学七年级(下)期中数学试卷(解析版): 这是一份2017-2018学年江苏省扬州市邗江区梅岭中学七年级(下)期中数学试卷(解析版),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












