冀教版八年级上册17.4 直角三角形全等的判定课前预习课件ppt

这是一份冀教版八年级上册17.4 直角三角形全等的判定课前预习课件ppt，共17页。PPT课件主要包含了情境导入，合作探究，或“HL”，条件1，条件2，课堂小结等内容，欢迎下载使用。

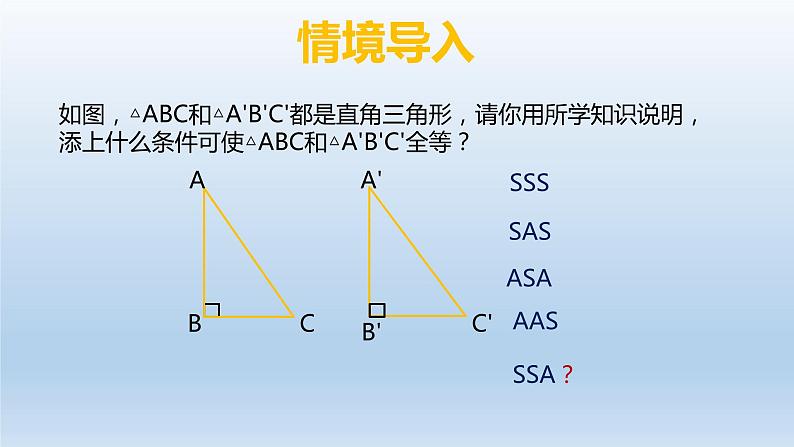
如图，△ABC和△A'B'C'都是直角三角形，请你用所学知识说明，添上什么条件可使△ABC和△A'B'C'全等？
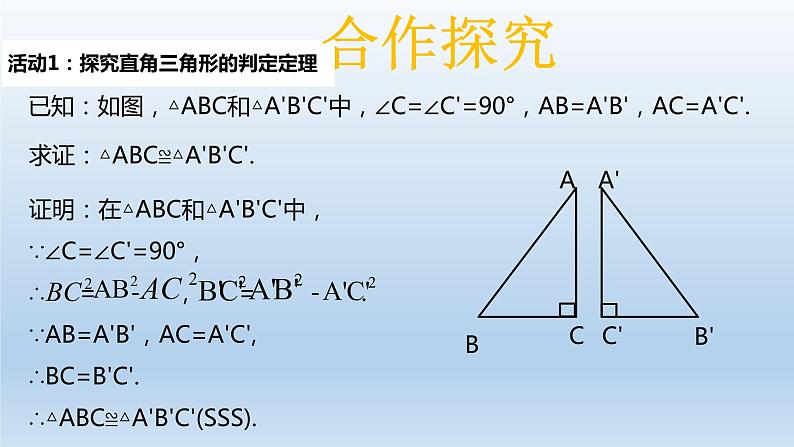
已知：如图，△ABC和△A'B'C'中，∠C=∠C'=90°，AB=A'B'，AC=A'C'.
求证：△ABC≌△A'B'C'.
证明：在△ABC和△A'B'C'中，∵∠C=∠C'=90°，∴ = － ， = － .∵AB=A'B'，AC=A'C',∴BC=B'C'.∴△ABC≌△A'B'C'(SSS).
活动1：探究直角三角形的判定定理
斜边和直角边对应相等的 两个直角三角形全等.
简写成“斜边、直角边”
直角三角形全等的判定定理
斜边和直角边对应相等的两个直角三角形全等。
在 Rt△ABC 和Rt △A'B'C' 中，
AB=A'B'AC=A'C'
Rt△ABC ≌ Rt △A'B'C'（HL）
跟踪训练（一）：判断题。
（1）有两条边分别相等的两个直角三角形是全等的。（ ）
（2）两直角边对应相等的两个直角三角形全等。（ ）
（3）有一条边和一个锐角分别相等的两个直角三角形是全等的。（ ）
例1已知一直角边和斜边,用尺规作直角三角形. 已知:如图所示,线段a,c.求作:△ABC,使∠C=90°,BC=a,AB=c.
作法:如图所示. (1)作线段CB=a.(2)过点C,作MC⊥BC.(3)以B为圆心,c为半径画弧,交CM于点A.(4)连接AB.则△ABC即为所求.
分析:首先作出边BC,由∠C为直角可以作出另一直角边所在的射线,由AB=c可以确定点A.
动动手 画一画 比比看
把我们刚画好的直角三角形剪（撕）下来，和同桌的比比看，这些直角三角形有怎样的关系呢？
结论:斜边和直角边对应相等的两个直角三角形全等
已知：如图，AC⊥BC， BD⊥AD， AC﹦BD， 求证：BC﹦AD.
请同学们仔细思考，二分之一互动交流，学生板演。
证明： ∵ AC⊥BC， BD⊥AD， ∴∠C=∠D=90°.
在 Rt△ABC 和Rt△BAD 中，
AB=BA, AC=BD .
∴ Rt△ABC≌Rt△BAD (HL).∴ BC﹦AD(全等三角形的对应边相等).
已知：如图，AC⊥BC， BD⊥AD， AC﹦BD， 求证：BC﹦AD.
请学生口述证明过程。
例2 已知：如图，点P在∠AOB的内部，PC⊥OA，PD⊥OB，垂足分别为C，D，PC=PD.求证：点P在∠AOB的平分线上.
活动3：角平分线性质定理的逆定理
请同学们独立思考，二分之一互动交流，学生板演。
证明：如图，作射线OP，∵PC⊥OA，PD⊥OB，∴∠PCO=∠PDO=90°.在Rt△OPC和Rt△OPD中，
OP=OP（公共边），
∴Rt△OPC≌Rt△OPD(HL).
∴∠POA=∠POB，∴OP是∠AOB的平分线，即点P在∠AOB的平分线上.
通过刚才的证明，同学们有没有想到我们学过的哪个知识点？你能对上边的证明过程进行简洁的概括吗？
角平分线性质定理的逆定理：到角的两边距离相等的点在这个角的平分线上。
跟踪训练（二）：如图 在△ABC中，已知BD⊥AC，CE ⊥AB，垂足分别为D,E， BD=CE.求证：AB=AC。
证明： ∵ BD⊥AC，CE⊥AB， ∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中，
∴ Rt△EBC≌Rt△DCB (HL).
∴ ∠EBC=∠DCB（全等三角形的对应边相等）.
∴ AB=AC（等角对等边）.
直角三角形全等的证明（HL）
斜边和一条直角边对应相等的两个直角三角形全等.
只须找除直角外的两个条件即可（两个条件中至少有一个条件是一对对应边相等）