2021届陕西省宝鸡市高三上学期理数高考模拟检测试卷(一)及答案

这是一份2021届陕西省宝鸡市高三上学期理数高考模拟检测试卷(一)及答案，共12页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
 高三上学期理数高考模拟检测试卷(一)
一、单项选择题
1.集合 ， ，那么 〔    〕
A.                       B.                       C.                       D. 
2.复数 ， ，那么 为〔    〕
A. 1                                         B.                                          C. 2                                         D. 
3.向量 ， ， ，假设 ，那么 〔    〕
A. 1                                         B.                                          C.                                          D. 2
4.很多关于大数的故事里(例如“棋盘上的学问〞，“64片金片在三根金针上移动的寓言〞)都涉及 这个数.请你估算这个数 大致所在的范围是〔    〕(参考数据： ， )
A.                      B.                      C.                      D. 
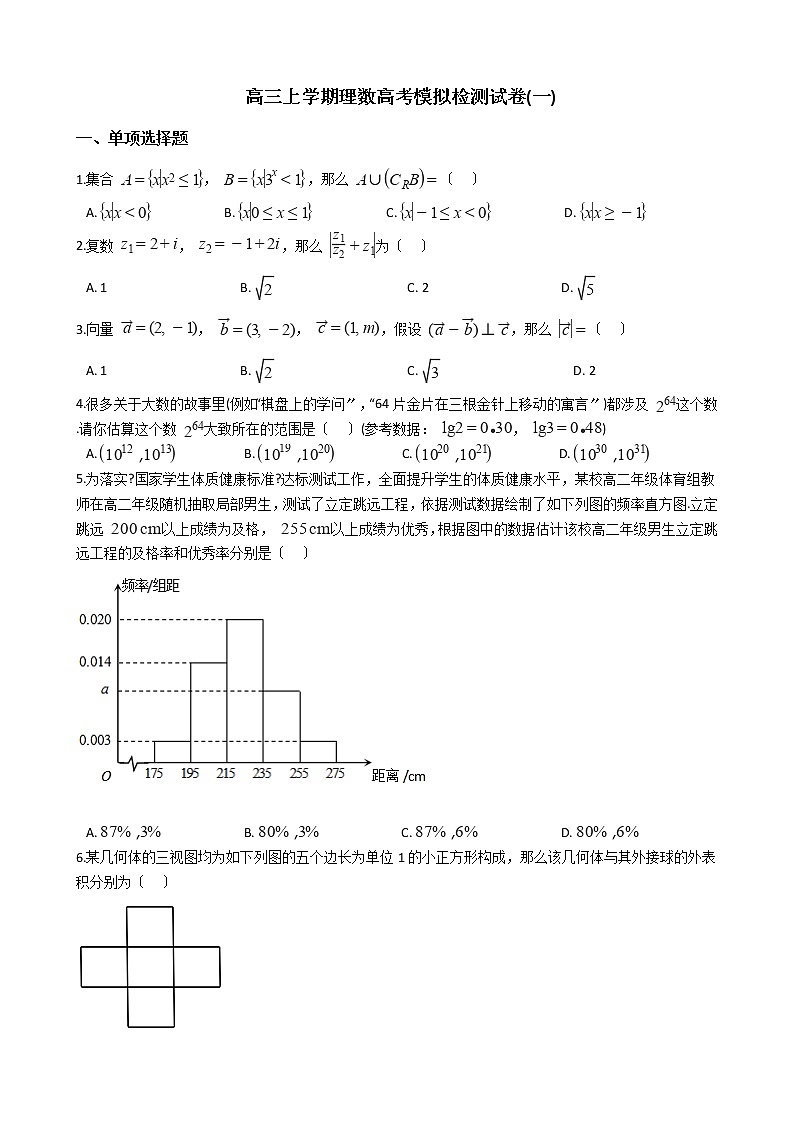
5.为落实?国家学生体质健康标准?达标测试工作，全面提升学生的体质健康水平，某校高二年级体育组教师在高二年级随机抽取局部男生，测试了立定跳远工程，依据测试数据绘制了如下列图的频率直方图.立定跳远 以上成绩为及格， 以上成绩为优秀，根据图中的数据估计该校高二年级男生立定跳远工程的及格率和优秀率分别是〔    〕


A.                          B.                          C.                          D. 
6.某几何体的三视图均为如下列图的五个边长为单位1的小正方形构成，那么该几何体与其外接球的外表积分别为〔    〕
 
A.                                B.                                C.                                D. 
7.过点 作圆 与圆 的切线，切点分别为 ､ ，假设 ，那么 的最小值为〔    〕
A.                                          B. 2                                         C.                                          D. 8
8.双曲线 的左､右焦点分别为 ， ，且以 为直径的圆与双曲线 的渐近线在第四象限交点为 ， 交双曲线左支于 ，假设 ，那么双曲线的离心率为〔    〕
A.                                    B.                                    C.                                    D. 
9.假设 ，那么 〔    〕
A.                                        B.                                        C.                                        D. 
10.假设 ， 满足约束条件 ，且 的最大值为 ，那么 的取值范围为〔    〕
A.                                 B.                                 C.                                 D. 
11.直线 和曲线 相切，那么 的取值范围是〔    〕
A.                     B.                     C.                     D. 
12.设 ， ， ，那么〔    〕
A.                                B.                                C.                                D. 以上均有可能
二、填空题
13.某“2021年宝鸡市防震减灾科普示范学校〞组织4名男生6名女生志愿者到社区进行防震减灾图片宣讲，假设这些选派学生只考虑性别，那么派往甲社区宣讲的3人中至少有2个男生概率为________.
14.记 为等比数列 的前 项和.设 ， ，那么 ________.
15.沿正三角形 的中线 翻折，使点 与点 间的距离为 ，假设该正三角形边长为 ，那么四面体 外接球外表积为________.
16.函数 是定义域为 上的奇函数，且对任意 ，都有 成立，当 时， ，那么 ________.当 时， ________.
三、解答题
17.设函数 .
〔1〕求 的最小正周期和值域.
〔2〕在锐角 中，角 ､ ､ 的对边长分别为 ､ ､ .假设 ， ，求 周长的取值范围.
18.如图三棱柱 中，底面 是边长为 的等边三角形， ， 分别为 ， 的中点， ， .

〔1〕证明： 平面 .
〔2〕求二面角 的平面角大小.
19.自从新型冠状病毒爆发以来，美国疫情持续升级，以下是美国2021年4月9日-12月14日每隔25天统计1次共11次累计确诊人数(万).
日期(月/日)
4/09
5/04
5/29
6/23
7/18
8/13
统计时间顺序
1
2
3
4
5
6
累计确诊人数






日期(月/日)
9/06
10/01
10/26
11/19
11/14
 
 
统计时间顺序
7
8
9
10
11
 
 
累计确诊人数





 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
〔1〕将4月9日作为第1次统计，假设将统计时间顺序作为变量 ，每次累计确诊人数作为变量 ，得到函数关系 ﹒对上表的数据作初步处理，得到局部数据已作近似处理的一些统计量的值 ， ， ， ， ， ， ， .根据相关数据，确定该函数关系式(函数的参数精确到 ).
〔2〕经过医学研究，发现新型冠状病毒极易传染，一个病毒的携带者在病情发作之前通常有长达14天的潜伏期，这个期间如果不采取防护措施，那么感染者与一位健康者接触时间超过15秒，就有可能传染病毒.如果一位新型冠状病毒的感染者传染给他人的概率为0.3，在一次36人的家庭聚餐中，只有一位感染者参加了聚餐，记余下的人员中被感染的人数为 ，求 最有可能(即概率最大)的值是多少.
20.抛物线 的焦点为 ，直线 与抛物线 交于 ， 两点.
〔1〕假设 ，求 的面积.
〔2〕圆 ，过点P〔4,4〕作圆M的两条切线，与曲线C交于另外两点分别为D，E，求证直线DE也与圆M相切.
21.函数 ，
〔1〕讨论函数 单调性.
〔2〕是 的导数， ，求证函数 存在三个零点.
22.以坐标原点为极点， 轴正半轴为极轴建立极坐标系.曲线 的极坐标方程为 ， ，曲线 的参数方程为 ( 的参数).
〔1〕将曲线 的极坐标方程､ 的参数方程化为普通方程.
〔2〕设 ， 的交点为 ，求圆心在极轴上，且经过极点和 的圆的极坐标方程.
23.函数 .
〔1〕当 时，求 的最小值.
〔2〕假设函数在区间 上递减，求 的取值范围.

答案解析局部
一、单项选择题
1.【解析】【解答】解：解不等式 得 ，故 ，
解不等式 得 ，故 ，
所以 。
故答案为：D.

【分析】利用一元二次不等式求解集的方法求出集合A，再利用指数函数的单调性结合与特殊值对应的指数的大小比较，从而求出集合B,再利用并集和补集的运算法那么，从而求出集合。
2.【解析】【解答】由题意，复数 ，
可得 ，
那么 。
故答案为：C.

【分析】利用复数的混合运算法那么结合复数求模公式，进而求出复数的模。
3.【解析】【解答】由题设可得 ，
因为 ，故 ，
解得 ，
所以 ，故 。
故答案为：B。

【分析】利用条件结合向量的坐标运算求出向量的坐标，再利用向量垂直数量积为0的等价关系，再结合数量积的坐标表示，从而求出m的值，进而求出向量的坐标，再利用向量的模的公式求出向量的模。
4.【解析】【解答】设 ，
那么 ，
所以 ，
所以 ，
故答案为：B。

【分析】利用条件设 ，再利用取对数的方法结合对数的运算法那么和指数与对数互化公式，进而求出x的值，从而估算出这个数 大致所在的范围。
5.【解析】【解答】由频率分布直方图可得,
优秀率为
，
及格率 ，
故答案为：C。

【分析】利用频率分布直方图结合各小组的矩形面积等于各小组的频率，从而估计出该校高二年级男生立定跳远工程的优秀率，再结合频率之和为1的性质，从而估计出该校高二年级男生立定跳远工程的及格率。
6.【解析】【解答】解：由三视图的几何体如下列图，

可知几何体的外表积为 ，
设该几何体外接球的半径为 ，那么 ，
所以该几何体外接球的外表积为 .
故答案为：C.

【分析】由三视图复原立体几何图形为正方体拼接的组合体，再利用组合体与外接球的位置关系，从而结合勾股定理求出该几何体外接球的半径，再结合球的外表积公式求出该几何体的外接球的外表积。再利用正方体的外表积公式结合求和的方法，注意重叠的局部不算为外表积的一局部，从而求出该几何体的外表积。
7.【解析】【解答】解：如下列图，

由圆的切线的性质得 ，
在 中有 ，
由题知 ，
，所以点 在线段 的垂直平分线上；
由题知 ，所以 与 的中点 的坐标为 ，
与 所在直线的斜率为 ，
所在直线 的斜率为 ，
直线 的方程为 ，即 ，
点 在 ，所以点 的坐标满足 ，
所以 ，
故答案为：B.

【分析】由圆的切线的性质得 ，在 中,结合勾股定理和条件求出，，所以点 在线段 的垂直平分线上，再利用两圆的标准方程求出两圆的圆心坐标，再结合中点坐标公式求出两圆心中点坐标，再利用两点求斜率公式求出圆心所在直线的斜率，再利用两直线垂直斜率之积等于-1，从而求出P,Q所在直线的斜率，再利用点斜式求出直线PQ的方程，再利用代入法结合点 在直线PQ上，从而将 转化为二次函数，从而用二次函数顶点式求最值的方法求出二次函数的最小值，进而求出 的最小值。
8.【解析】【解答】 ，圆方程为 ，
由 ， 由 ， ，解得 ，即 ，
设Q(x0 ， y0)，由 ， ，得 ， ，
因为 在双曲线上，
∴ ， ，
解得 〔 舍去〕，
故答案为：A。

【分析】利用双曲线标准方程确定焦点的位置，从而求出焦点坐标和渐近线方程，再利用中点坐标公式结合两点求距离公式，从而求出以 为直径的圆的圆心坐标和半径长，从而求出圆的标准方程，再利用以 为直径的圆与双曲线 的渐近线在第四象限交点为 ， 联立二者方程结合双曲线中a,b,c三者的关系式，从而求出点P的坐标，再利用共线向量的坐标表示结合条件，从而求出点Q的坐标，再利用点Q在双曲线上结合代入法，从而求出a,c的关系式，再利用离心率公式变形求出双曲线的离心率。
9.【解析】【解答】 ，
。
故答案为：A。

【分析】利用条件结合诱导公式，从而求出的值，再利用二倍角的余弦公式，从而求出的值。
10.【解析】【解答】解：由约束条件得如下列图区域，

，代入 ，
得 ，解得 。
故答案为：D.

【分析】利用二元一次不等式画出可行域，再利用可行域找出最优解，再利用最优解求出线性目标函数的最大值，再结合线性目标函数 的最大值为 ， 从而求出a的值。
11.【解析】【解答】设切点是 ,
由 ,
那么以P为切点的切线方程为 ,
因为该切线过原点，所以 ，
所以 ,
所以a0，再利用圆经过极点和 ， 结合圆的半径相等和两点距离公式，从而求出a的值，进而求出圆心坐标，再利用勾股定理求出圆的半径，进而求出圆的标准方程，再利用极坐标与直角坐标的互化公式，从而求出圆心在极轴上，且经过极点和 的圆的极坐标方程。
23.【解析】【分析】〔1〕利用a的值求出函数的解析式，再利用绝对值的定义将函数转化为分段函数，再利用分段函数的解析式结合分类讨论的方法，从而求出分段函数的最小值。
〔2〕利用分类讨论的方法结合分段函数的图象，从而结合分段函数在区间 上递减， 从而求出实数a的取值范围。