2021届四川省内江市高三理数第三次模拟试卷及答案

这是一份2021届四川省内江市高三理数第三次模拟试卷及答案，共13页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
 高三理数第三次模拟试卷
一、单项选择题
1.复数  (i为虚数单位)的共轭复数是〔   〕

A. 1+i                                     B. 1−i                                     C. −1+i                                     D. −1−i
2.集合 ， ，那么集合 可以是〔    〕
A.                                  B.                                  C.                                  D. 
3.平面向量 、 、 满足 ，且 ，那么 的值为〔   〕
A.                                      B.                                      C.                                      D. 
4.为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分〔十分制〕如下列图，假设得分值的中位数为 ，众数为 ，平均值为 ，那么〔   〕

A.                   B.                   C.                   D. 
5.在 中， ， ， ，那么 边上的高等于〔    〕
A.                                       B.                                       C.                                       D. 
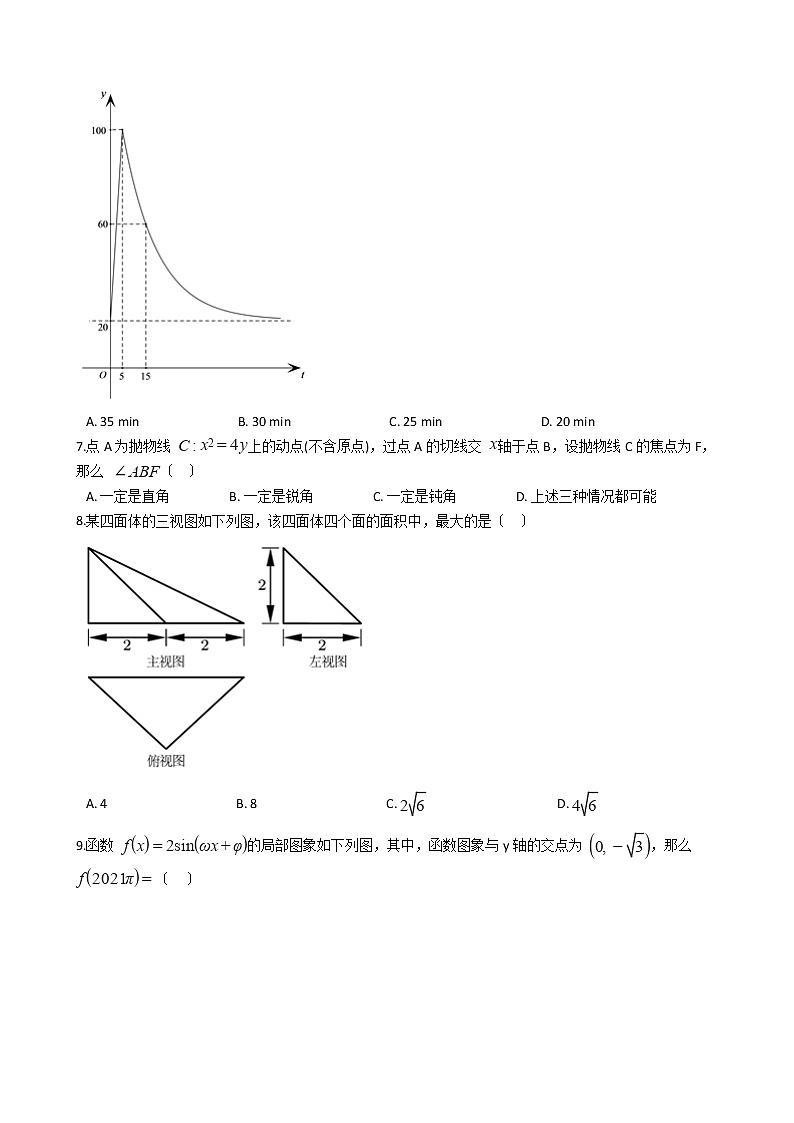
6.某种热饮需用开水冲泡，其根本操作流程如下：①先将水加热到100℃，水温 与时间t〔min〕近似满足一次函数关系；②用开水将热饮冲泡后在室温下放置，温度 与时间t〔min〕近似满足函数的关系式为 〔 为常数〕, 通常这种热饮在40℃时，口感最正确，某天室温为20℃时，冲泡热饮的局部数据如下列图，那么按上述流程冲泡一杯热饮，并在口感最正确时饮用，最少需要的时间为

A. 35 min                               B. 30 min                               C. 25 min                               D. 20 min
7.点A为抛物线 上的动点(不含原点)，过点A的切线交 轴于点B，设抛物线C的焦点为F，那么 〔   〕
A. 一定是直角                  B. 一定是锐角                  C. 一定是钝角                  D. 上述三种情况都可能
8.某四面体的三视图如下列图，该四面体四个面的面积中，最大的是〔   〕

A. 4                                        B. 8                                        C.                                         D. 
9.函数 的局部图象如下列图，其中，函数图象与y轴的交点为 ，那么 〔    〕

A.                                     B.                                     C.                                     D. 
10.直线l：y＝m〔x﹣2〕+2与圆C：x2+y2＝9交于A，B两点，那么使弦长|AB|为整数的直线l共有〔    〕
A. 6条                                       B. 7条                                       C. 8条                                       D. 9条
11.椭圆C： 的右焦点F，点P在椭圆C上，点Q在圆E：(x＋3)2＋(y－4)2＝4上，且圆E上的所有点均在椭圆C外，假设|PQ|－|PF|的最小值为2 －6，且椭圆C的长轴长恰与圆E的直径长相等，那么椭圆C的标准方程为〔    〕
A.                       B.                       C.                       D. 
12.，记 ， ， ，那么 、 、 的大小关系为〔    〕
A.                            B.                            C.                            D. 
二、填空题
13.假设实数 满足约束条件 ，那么 的最大值是________．
14.二项式 的展开式中的常数项是________.〔用数字作答〕
15.现为一球状巧克力设计圆锥体的包装盒，假设该巧克力球的半径为3，那么其包装盒的体积的最小值为________．
16.数学中有许多形状优美､寓意美好的曲线，如图：四叶草曲线 就是其中一种，其方程为 .给出以下四个结论：

①曲线C有四条对称轴；
②曲线C上的点到原点的最大距离为 ；
③在第一象限内，过曲线C上一点作两坐标轴的垂线与两坐标轴围成的矩形面积的最大值为 ；
④四叶草面积小于 .
其中，所有正确结论的序号是________.
三、解答题
17.等差数列 的公差 ，它的前 项和为 ，假设 ，且 ， ， 成等比数列.
〔1〕求数列 的通项公式；
〔2〕设数列 的前 项和为 ，求证： .
18.某大学生参加社会实践活动，对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查，销售单价x和销售量y之间的一组数据如下表所示：
月份
1
2
3
4
5
6
销售单价〔元〕
9

10

11
8
销售量〔件〕
11
10
8
6
5

〔1〕根据1至5月份的数据，求出y关于x的回归直线方程；
〔2〕假设由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元，那么认为所得到的回归直线方程是理想的，试问〔1〕中所得到的回归直线方程是否理想？
〔3〕预计在今后的销售中，销售量与销售单价仍然服从〔1〕中的关系，假设该种机器配件的本钱是2.5元/件，那么该配件的销售单价应定为多少元才能获得最大利润？〔注：利润=销售收入-本钱〕．
参考公式：回归直线方程 ,其中 ，
19.如图，在四棱锥 中， 平面 ， ， ， ， . 为 的中点，点 在 上，且 .

〔1〕求证： 平面 ；
〔2〕求二面角 的余弦值；
〔3〕设点 在 上，且 .判断点 是否在平面 内，说明理由.
20.椭圆 过点 .
〔1〕求椭圆 的方程；
〔2〕过点 作 轴的垂线 ，设点 为第四象限内一点且在椭圆 上〔点 不在直线 上〕，直线 关于 的对称直线 与椭圆交于另一点 .设 为坐标原点，判断直线 与直线 的位置关系，并说明理由.
21.设函数
〔1〕讨论 的单调性；
〔2〕假设 有两个极值点 和 ，记过点 的直线的斜率为 ，问：是否存在 ，使得 ？假设存在，求出 的值，假设不存在，请说明理由．
22.在直角坐标系 中，直线 的参数方程为 〔 为参数〕，以原点 为极点， 轴的正半轴为极轴建立极坐标系，曲线 的极坐标方程为
〔1〕求曲线 的直角坐标方程，并指出其表示何种曲线；
〔2〕设直线 与曲线 交于 两点，假设点 的直角坐标为 ，试求当 时， 的值.
23. ．
〔1〕求 的最小值；
〔2〕假设 对满足题中条件的 恒成立，求实数 的取值范围．

答案解析局部
一、单项选择题
1.【解析】【解答】详解： ，∴共轭复数为 ，
故答案为：B.
【分析】由复数的除法运算化简复数为a+bi〔a，b∈R〕的形式，那么其共轭复数可求．
2.【解析】【解答】集合 ， .
对于A选项， ，那么 ，不符合题意；
对于B选项， ，那么 ，不符合题意；
对于C选项， ，那么 ，符合题意；
对于D选项， ，那么 ，不符合题意.
故答案为：C.

【分析】进行交集的运算即可得出答案。
3.【解析】【解答】由 可得 ，等式两边平方得 ，即 ，
因此， .
故答案为：A.

【分析】根据条件可得出， 两边平方进行数量积的运算即可求出   的值 。
4.【解析】【解答】试题分析：由图可知，30名学生的得分情况依次为：2个人得3分，3个人得4分，10个人得5分，6个人得6分，3个人得7分，2个人得8分，2个人得9分，2个人得10分．中位数为第15,16个数〔分别为5,6〕的平均数，即 ＝5.5,5出现的次数最多，故 ＝5， ≈5.97
于是得 .
故答案为：D

【分析】 观察频数分布直方图，结合中位数、众数的概念，得出中位数为第15，16名学生的成绩(分别为5，6)的平均数，众数为出现次数最多的数据，据此可求得  、   的值，再根据平均数的计算公式可得该组数据的平均数。
5.【解析】【解答】在 中， ， ， ，
由余弦定理可得： ，
可得 ，
设 边上的高为h，那么 ，
即 ，解得： .
故答案为：B.

【分析】 由及余弦定理可求cosA的值，进而利用同角三角函数根本关系式可求sinA的值，设AB边上的高为h,利用三角形面积公式即可计算得解.
6.【解析】【解答】由题意，当0≤t≤5时，函数图象是一个线段，当t≥5时，函数的解析式为 ，
点〔5，100〕和点〔15，60〕，代入解析式，
有 ，
解得a＝5,b=20，
故函数的解析式为 ，t≥5．令y=40，解得t=25,
∴最少需要的时间为25min．
故答案为：C.

【分析】 根据条件结合函数图象，利用待定系数法求出函数的解析式，令y=40进行求解即可 .
7.【解析】【解答】试题分析： ,设 ，那么过点 的切线方程为 ，令 ，得 ，即点 ，又 ，于是 ， ，所以 ，
故答案为：A．

【分析】 求导数，确定过A的切线方程，可得B的坐标，求出， 可得，即可得出结论.
8.【解析】【解答】根据几何体的三视图复原得到该几何体的直观图为：该几何体为三棱锥体．
如下列图：

由于 ，下底面 为等腰直角三角形．
可得 ， ， ， ，
所以该四面体四个面的面积中，最大的是 ．
故答案为：C．

【分析】根据几何体的三视图复原得到该几何体的直观图为：该几何体为三棱锥体，画出图形求出四个面的面积即可。
9.【解析】【解答】由图象可得 ，可得 ，
由于函数 在 附近单调递增，那么 ，
那么 ，
，可得 ，
所以， ，
由图象可知，函数 的最小正周期 满足 ，可得 ，
即 ，解得 ，即 ，
，那么 ，可得 ，从而 ，
因此， .
故答案为：A.

【分析】 将点   的坐标代入解析式可求得φ的值，由图象可知，函数 的最小正周期 满足 ，可得 ， 求出， 进而得到f (x )的解析式，即可得出 。
10.【解析】【解答】根据题意，直线恒过点M〔2，2〕，圆C：x2+y2＝9的圆心C为〔0，0〕，半径r＝3，
那么CM＝2
当直线与CM垂直时，M为|AB|中点，此时|AB|＝2 2，符合题意，此时直线有一条，
当直线过圆心C时，|AB|＝2r＝6，满足题意，此时直线有一条，
那么当|AB|＝3，4，5时，各对应两条直线，
综上，共8条直线.
故答案为：C.

【分析】 根据题意，直线过点M (2, 2)，圆C的圆心(0，0)，半径r=3，那么可得当直线与CM垂直时，即M为AB的中点时，弦长|AB|最短，求出直线CM的斜率，由直线垂直与斜率的关系分析可得直线AB的斜率，由直线的点斜式方程分析可得答案.
11.【解析】【解答】因为圆E：(x＋3)2＋(y－4)2＝4的半径为2，所以 ，
设椭圆的左焦点为 ，由椭圆的定义可得 ，

所以 ，
所以 ，当且仅当 四点共线时，等号成立，
又|PQ|－|PF|的最小值为2 －6，所以 ，即 ，
所以 ，解得 或 〔舍〕.
所以 ，
所以椭圆C的标准方程为 .
故答案为：C.
【分析】因为圆E：(x＋3)2＋(y－4)2＝4的半径为2，所以 ，由椭圆的定义可得 ,根据题意可得当且仅当 四点共线时，|PQ|－|PF|取得最小值为 ，所以 ，由此可解得结果.
12.【解析】【解答】构造函数 ，其中 ，那么 ，
令 ，其中 ，那么 ，
所以，函数 在 上单调递减，那么 ，
所以， 对任意的 恒成立，所以，函数 在 为减函数，
因为 ，那么 ，那么 ，即 ，
构造函数 ，其中 ，那么 ，
所以，函数 在 上单调递增，那么 ，即 ，
所以， ，那么 ，所以， .
综上所述， .
故答案为：C.

【分析】利用导数研究其单调性即可得出答案。
二、填空题
13.【解析】【解答】作出可行域，如图 内部〔含边界〕，作直线 ，由 得 ，

直线向下平移时，纵截距减小， 增大，
所以平移直线 ，当直线 过点 时， ．
故答案为：3．

【分析】 由题意画出约束条件表示的平面区域，目标函数  变形为，平移目标函数，找出最优解，求出最大值.
14.【解析】【解答】有题意可得，二项式展开式的通项为：
 
令 可得 ，此时 .
【分析】根据二项式展开式的通项公式求解.
15.【解析】【解答】轴截面如图，设 那么
， ，当 时， ．填 ．

【分析】设 ， 根据体积公式及根本不等式即可求出包装盒的体积的最小值 。
16.【解析】【解答】①；以 代 ， 不变代入方程中得， ，
所以图形关于纵轴对称；
以 代 ， 不变代入方程中得， ，所以图形关于横轴对称；
以 代 ，以 代 代入方程中得： ，所以图象关于直线 对称；
以 代 ，以 代 代入方程中得：
，所以图象关于直线 对称，因此图象有四个对称轴，故结论正确；
②：由对称轴性不妨设四叶草曲线与直线 在第一象限的交点为 ，
，
所以曲线 上的点到原点的最大距离为 ，故本结论不正确；
③：在第一象限内，设曲线 上一点 ，
因为 ，所以 〔当且仅当 时，取等号〕，所以本结论正确；
④：通过②可知：四叶草曲线在以原点为圆心半径为 的圆内及圆上，所以四叶草的面积小于圆的面积 ，故本结论正确，
故答案为：①③④

【分析】 通过方程中的x，y的变换，求得四叶草曲线的对称轴，可判断①;由y=x与 联立，解方程，结合两点的距离公式计算可判断②;设出第一象限的一-点，运用根本不等式即可得到最大值可判断③;由四叶草曲线在以原点为圆心，为半径的圆内，计算可判断④。
三、解答题
17.【解析】【分析】 (1)依题意，可由 求得其首与公差，继而可求得数列{an}的通项公式；
(2) 由(1) 可得 ，  用裂项法可求得   
，从而可求得  ，利用递增函数的定义再证明数列 是递增数列，即可证得结论.
 
 
18.【解析】【分析】〔1〕计算， 求出回归系数，写出回归直线方程；
〔2〕根据回归直线方程，计算对应的数值，判断回归直线方程是否理想；
〔3〕求销售利润函数 ，根据二次函数的图像与性质求最大值即可。
 
19.【解析】【分析】 (1)利用线面垂直的性质定理得到PA⊥CD,由条件结合线面垂直的判定定理证明即可;
(2)建立适宜的空间直角坐标系，求出所需各点的坐标，利用待定系数法求出平面AEF和平面PAD的法向量，由二面角的求解公式计算即可;
(3) 利用 即可得到直线AG在平面AEF内，从而得到点G在平面AEF内.
20.【解析】【分析】〔1〕将点   代入到椭圆方程，解得a的值，即可得出椭圆  的方程；
〔2〕设直线  ，  ，设点  、  ，
将直线与椭圆联立，得到x1和x2，从而得到AB的斜率，得到 ，得到直线AB与直线OP平行。
 
21.【解析】【分析】〔1〕利用求导的方法判断函数的单调性，从而结合分类讨论的方法函数讨论出 的单调性。
〔2〕利用求导的方法判断函数的单调性，从而求出函数的极值点，再利用条件函数 有两个极值点 和 ，再利用反证法，假设存在 ，使得 ，再利用两点求斜率公式结合〔1〕中函数的单调性，从而推出矛盾，进而推出 不存在 ，使得 。
22.【解析】【分析】 (1)利用参普互化公式将曲线C的方程化为一般方程，进而得到圆心半径；
(2)联立直线和圆的方程，得到关于t的二次方程，结合韦达定理求出结果即可.
 
 
23.【解析】【分析】〔1〕由   得   ，那么 ， 从而利用根本不等式可得结果；
〔2〕由〔1〕得 ， 分三种情况讨论，分别求解不等式组，然后求并集即可得结果。