2021届河南省六市高三理数第二次联考（二模）试卷及答案

这是一份2021届河南省六市高三理数第二次联考（二模）试卷及答案，共12页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
高三理数第二次联考〔二模〕试卷
一、单项选择题
1.复数 的实部为〔    〕
A. -1                                          B. 1                                          C. -2                                          D. 2



2.全集 ，集合 ， ，那么 〔    〕
A.                                     B.                                     C.                                     D. 



3.在五场篮球比赛中，甲、乙两名运发动得分的茎叶图如下列图，以下说法正确的选项是〔    〕

A. 甲的平均得分比乙多，且甲比乙稳定

                  B. 甲的平均得分比乙多，但乙比甲稳定


C. 乙的平均得分比甲多，且乙比甲稳定

                  D. 乙的平均得分比甲多，但甲比乙稳定



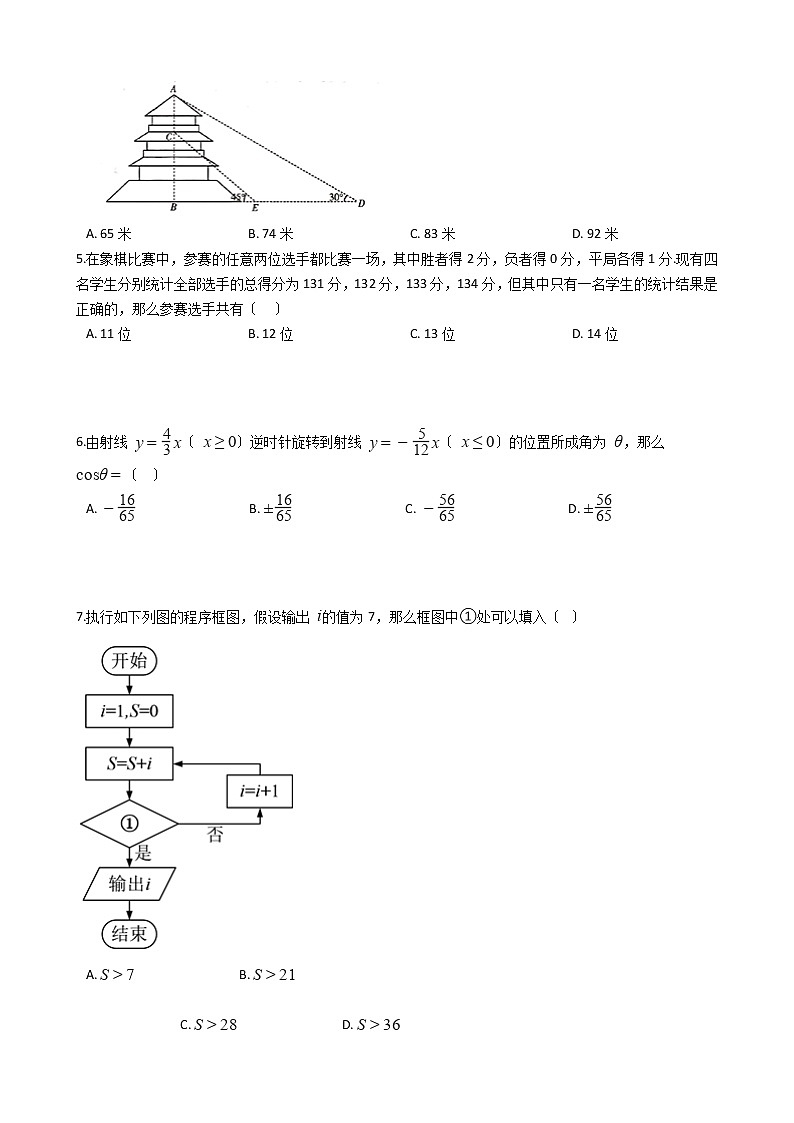
4.“欲穷千里目，更上一层楼〞出自唐朝诗人王之涣的?登鹳雀楼?，鹳雀楼位于今山西永济市，该楼有三层，前对中条山，下临黄河，传说常有鹳雀在此停留，故有此名．下面是复建的鹳雀楼的示意图，某位游客〔身高忽略不计〕从地面 点看楼顶点 的仰角为30°，沿直线前进79米到达 点，此时看点 的仰角为45°，假设 ，那么楼高 约为〔    〕．

A. 65米                                    B. 74米                                    C. 83米                                    D. 92米
5.在象棋比赛中，参赛的任意两位选手都比赛一场，其中胜者得2分，负者得0分，平局各得1分.现有四名学生分别统计全部选手的总得分为131分，132分，133分，134分，但其中只有一名学生的统计结果是正确的，那么参赛选手共有〔    〕
A. 11位                                    B. 12位                                    C. 13位                                    D. 14位



6.由射线 〔 〕逆时针旋转到射线 〔 〕的位置所成角为 ，那么 〔   〕
A.                                    B.                                    C.                                    D. 



7.执行如下列图的程序框图，假设输出 的值为7，那么框图中①处可以填入〔   〕

A.                                  B. 

                                 C.                                  D. 



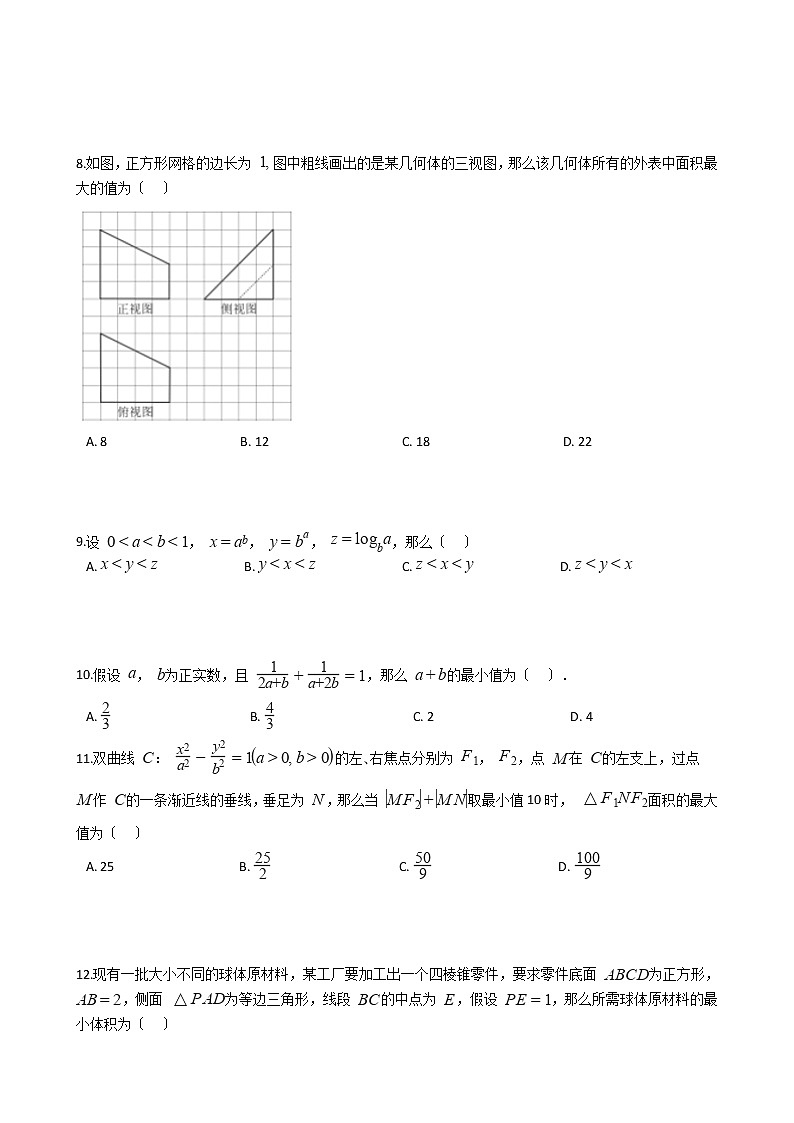
8.如图，正方形网格的边长为 图中粗线画出的是某几何体的三视图，那么该几何体所有的外表中面积最大的值为〔    〕

A. 8                                         B. 12                                         C. 18                                         D. 22



9.设 ， ， ， ，那么〔    〕
A.                            B.                            C.                            D. 



10.假设 ， 为正实数，且 ，那么 的最小值为〔    〕．
A.                                            B.                                            C. 2                                           D. 4
11.双曲线 ： 的左､右焦点分别为 ， ，点 在 的左支上，过点 作 的一条渐近线的垂线，垂足为 ，那么当 取最小值10时， 面积的最大值为〔    〕
A. 25                                       B.                                        C.                                        D. 



12.现有一批大小不同的球体原材料，某工厂要加工出一个四棱锥零件，要求零件底面 为正方形， ，侧面 为等边三角形，线段 的中点为 ，假设 ，那么所需球体原材料的最小体积为〔    〕
A.                                    B. 

                                   C.                                    D. 



二、填空题
13. ， 为单位向量，且 ，那么向量 与 的夹角为________.
14.直线 与圆 相交于 ， 两点，且 为等腰直角三角形，那么实数 的值为________
15. 内角 ， ， 所对的边分别为 ， ， ，假设 ， ， ，那么 面积为________.
16.假设 ，不等式 恒成立，那么 的最大值为________.
三、解答题
17.设数列 是公差大于零的等差数列， ， .
〔1〕求数列 的通项公式；
〔2〕设数列 满足 ，求 .
18.如下列图，在四棱锥 中， ， ， ，且 ， ．

〔1〕平面 ；
〔2〕在线段 上，是否存在一点 ，使得二面角 的大小为 ？如果存在，求 的值；如果不存在，请说明理由．
19.2021年席卷全球的新冠肺炎给世界人民带来了巨大的灾难，面对新冠肺炎，早发现、早诊断、早隔离、早治疗是有效防控疾病蔓延的重要举措之一.某社区对55位居民是否患有新冠肺炎疾病进行筛查，先到社区医务室进行口拭子核酸检测，检测结果成阳性者，再到医院做进一步检查，随机一人其口拭子核酸检测结果成阳性的概率为2%，且每个人的口拭子核酸是否呈阳性相互独立.
〔1〕假设该疾病患病的概率是0.3%，且患病者口拭子核酸呈阳性的概率为98%，设这558位居民中有一位的口拭子核酸检测呈阳性，求该居民可以确诊为新冠肺炎患者的概率；
〔2〕根据经验，口拭子核酸检测采用分组检测法可有效减少工作量，具体操作如下：将55位居民分成假设干组，先取每组居民的口拭子核酸混在一起进行检测，假设结果显示阴性，那么可断定本组居民没有患病，不必再检测；假设结果显示阳性，那么说明本组中至少有一位居民患病，需再逐个进行检测，现有两个分组方案：
方案一：将55位居民分成11组，每组5人；
方案二：将55位居民分成5组，每组11人；
试分析哪一个方案的工作量更少？
〔参考数据： ， 〕
20.圆 ，动圆 与圆 相外切，且与直线 相切.
〔1〕求动圆圆心 的轨迹 的方程.
〔2〕点 ，过点 的直线 与曲线 交于两个不同的点 〔与 点不重合〕，直线 的斜率之和是否为定值？假设是，求出该定值；假设不是，说明理由.
21.函数 ， .
〔1〕设 图象在点 处的切线与 的图象相切，求 的值；
〔2〕假设函数 存在两个极值点 ， ，且 ，求 的最大值.
22.在平面直角坐标系 中，直线 的参数方程为 ( 为参数， ).以坐标原点为极点， 轴正半轴为极轴建立极坐标系，曲线 的极坐标方程为 .
〔1〕求直线 的普通方程和曲线 的直角坐标方程；
〔2〕设直线 与曲线 交于 ､ 两点，求 面积的最大值.
23.函数 .
〔1〕当 时，解不等式 ；
〔2〕假设存在 ，使得不等式 的解集非空，求b的取值范围.

答案解析局部
一、单项选择题
1.【解析】【解答】 的实部为-1，
故答案为：A.
【分析】 利用复数的运算法那么求出i〔2+i〕=-1+2i．由此能求出复数i〔2+i〕的实部．
2.【解析】【解答】由 ，得 ，
又因为 ，
所以 ，
所以 ，
故答案为：B.

【分析】 化简集合B，根据补集与交集的定义计算即可．
3.【解析】【解答】由茎叶图可知，甲运发动的平均分为 ，
方差为 ，
乙运发动的平均得分为 ，
方差为 .
因此，乙的平均得分比甲多，且乙比甲稳定.
故答案为：C.

【分析】 由茎叶图，数据的稳定程度与茎叶图形状的关系，茎叶图中各组数据大局部集中在某个叶上，表示该组数据越稳定，根据数据可直接判断最高分的大小．
4.【解析】【解答】设 的高度为 ，
那么由可得 ， ， ，
所以 ，解得 ，
所以楼高 〔米〕．
故答案为：B．

【分析】设 的高度为 ，然后得到， 再根据， 求出的值即可。
5.【解析】【解答】设参赛选手共有 位，那么总比赛场次为 ，即 场，且 ， ，
由题意知：任意一场比赛结束，选手的总得分为2分，故所有选手总得分为 分且为偶数，
∴当 ，得 ；当 ， 无整数解；
∴ (位).
故答案为：B.

【分析】 由题意，由于 胜者得2分，负者得0分，平局各得1分 ，所以每场比赛都会产生2分，那么最后总分一定为偶数，所以131和133被排除，剩下132和134，再进行判断.
6.【解析】【解答】解：设 〔 〕的倾斜角为 ，那么
射线 〔 〕的倾斜角为 ，
∴
故答案为：A

【分析】 根据直线l1到l2的角的正切公式求出tanθ ， 再利用同角的三角函数关系求出cosθ的值．
7.【解析】【解答】由程序流程图，其执行逻辑及对应输出如下：
⒈ ：输出 ，执行循环，那么 ；
⒉ ：输出 ，执行循环，那么 ；
⒊ ：输出 ，执行循环，那么 ；
⒋ ：输出 ，执行循环，那么 ；
⒌ ：输出 ，执行循环，那么 ；
⒍ ：输出 ，执行循环，那么 ；
⒎ ：输出 ，此时根据条件跳出循环，输出 .
∴只有B：当 符合要求.
故答案为：B.

【分析】 据程序框图写出几次循环的结果，直到i=7，即可得出①满足的条件．
8.【解析】【解答】由三视图可知该几何体为图中的三棱台 ，

根据三视图可知，正方体的棱长为4， 分别为 的中点.
侧面 为全等的两个直角梯形,即面积为： .
设 相交于 , 相交于 ，那么 分别为 的中点.
侧面 是等腰梯形，如图在矩形 中， ,
所以 平面 ，那么 ,所以梯形 的高为
取 的中点 ,那么 ,所以
其面积为
该几何体所有的外表中最大的值为18.
故答案为：C

【分析】由三视图，在正方体中将该几何体复原，然后再计算出面积最大的面。
9.【解析】【解答】因为
令
那么


将式子变形可得 ，
因为
所以
由对数函数的图像与性质可知
综上可得
故答案为：A.

【分析】 根据0