2021届山东省日照市高三下学期数学一模试卷及答案

这是一份2021届山东省日照市高三下学期数学一模试卷及答案，共17页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

 高三下学期数学一模试卷
一、单项选择题
1.复平面内表示复数 〔 〕的点位于〔    〕
A. 第一象限                           B. 第二象限                           C. 第三象限                           D. 第四象限



2.设集合 ， ，那么 〔    〕
A.                             B.                             C.                             D. 



3.要将甲、乙、丙、丁4名同学分到 、 、 三个班级中，要求每个班级至少分到一人，那么甲被分到 班的分法种数为〔   〕
A.                                          B.                                          C.                                          D. 
4.明朝早期，郑和七下西洋过程中，将中国古代天体测量方面所取得的成就创造性地应用于航海，形成了一套先进的航海技术——“过洋牵星术〞，简单地说，就是通过观测不同季节、时辰的日月星辰在天空运行的位置和测量星辰在海面以上的高度来判断水位.其采用的主要工具是牵星板，其由12块正方形模板组成，最小的一块边长约2厘米〔称一指〕，木板的长度从小到大依次成等差数列，最大的边长约24厘米〔称十二指〕.观测时，将木板立起，一手拿着木板，手臂伸直，眼睛到木板的距离大约为72厘米，使牵星板与海平面垂直，让板的下缘与海平面重合，上边缘对着所观测的星辰依上下不同替换、调整木板，当被测星辰落在木板上边缘时所用的是几指板，观测的星辰离海平面的高度就是几指，然后就可以推算出船在海中的地理纬度.如下列图，假设在一次观测中，所用的牵星板为六指板，那么 约为〔    〕

A.                                         B.                                         C.                                         D. 



5.函数 〔 ，且 〕的图象恒过定点 ，假设点 在椭圆 〔 ， 〕上，那么 的最小值为〔    〕
A. 12                                         B. 14                                         C. 16                                         D. 18



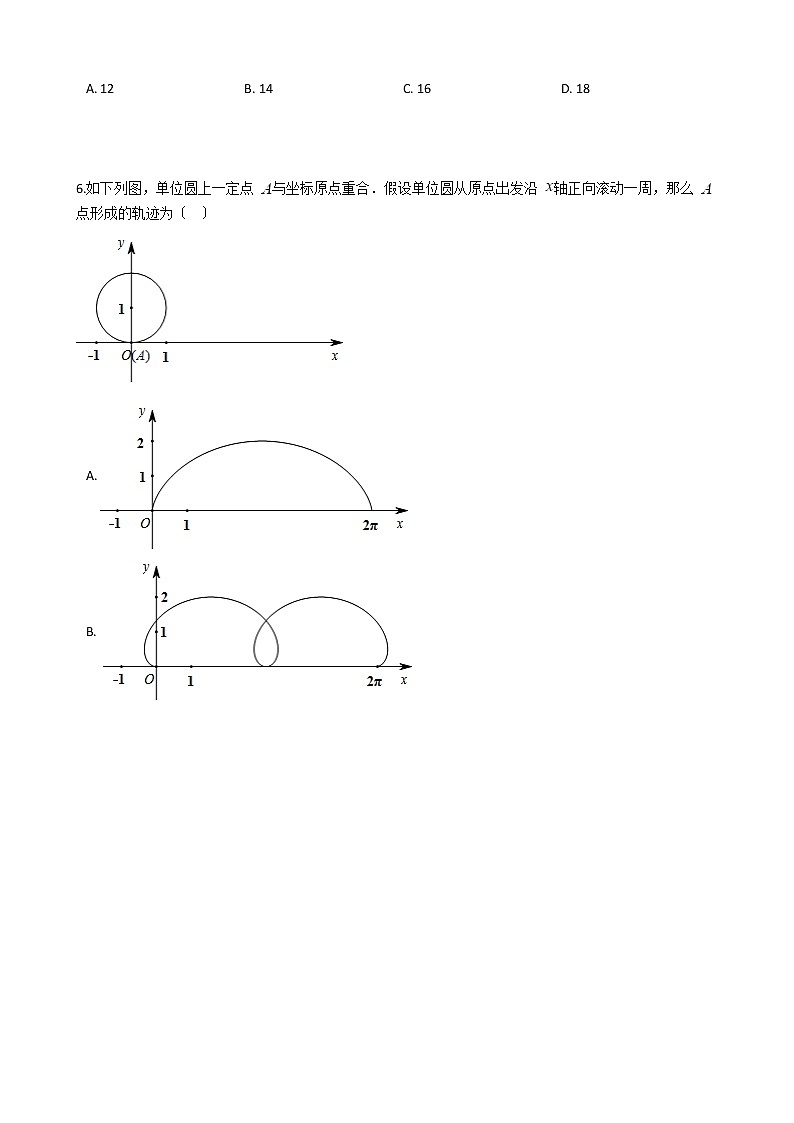
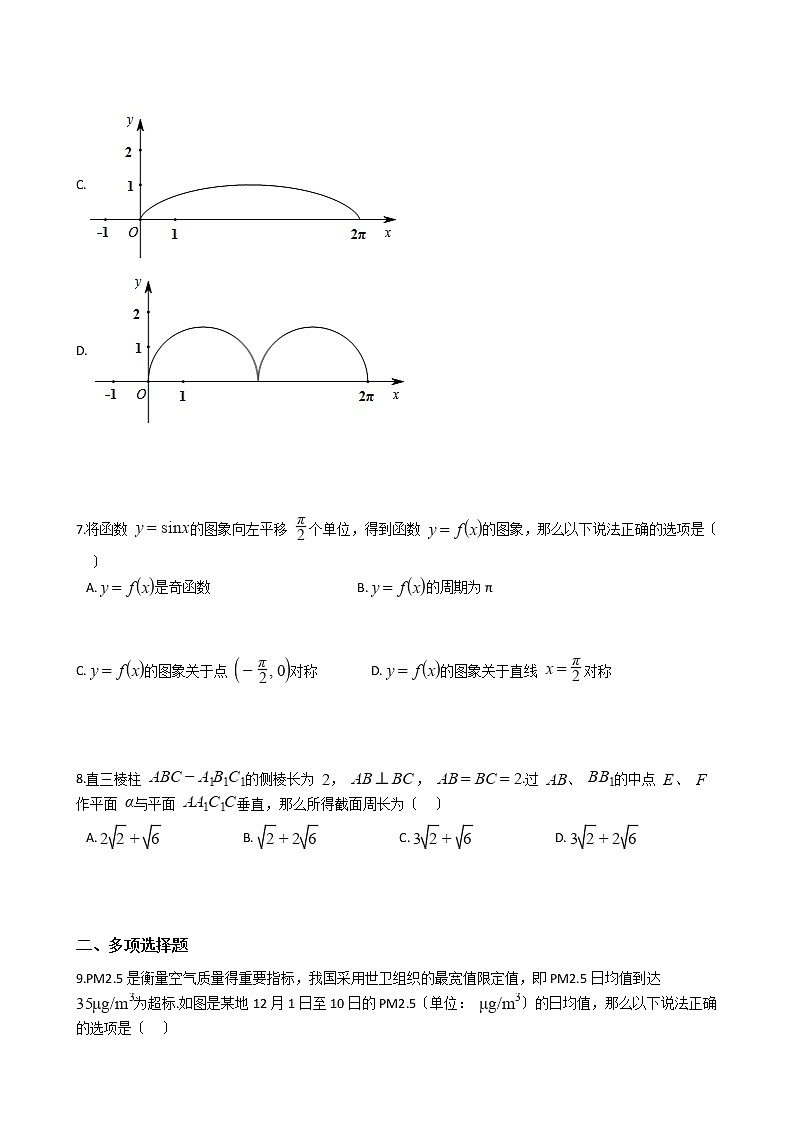
6.如下列图，单位圆上一定点 与坐标原点重合．假设单位圆从原点出发沿 轴正向滚动一周，那么 点形成的轨迹为〔   〕

A. 
B. 


C. 
D. 



7.将函数 的图象向左平移 个单位，得到函数 的图象，那么以下说法正确的选项是〔    〕
A. 是奇函数                                              B. 的周期为π


C. 的图象关于点 对称                D. 的图象关于直线 对称



8.直三棱柱 的侧棱长为 ， ， .过 、 的中点 、 作平面 与平面 垂直，那么所得截面周长为〔    〕
A.                          B.                          C.                          D. 



二、多项选择题
9.PM2.5是衡量空气质量得重要指标，我国采用世卫组织的最宽值限定值，即PM2.5日均值到达 为超标.如图是某地12月1日至10日的PM2.5〔单位： 〕的日均值，那么以下说法正确的选项是〔    〕

A. 这10天中有3天空气质量为一级


B. 从6日到9日PM2.5日均值逐渐降低


C. 这10天中PM2.5日均值的中位数是55


D. 这10天中PM2.5日均值的平均值是45



10. ， ，那么〔    〕
A.            B. 

           C.            D. 



11.函数 对于任意 ，均满足 .当 时 ，假设函数 ，以下结论正确的为〔    〕
A. 假设 ，那么 恰有两个零点

                       B. 假设 ，那么 有三个零点


C. 假设 ，那么 恰有四个零点

                D. 不存在 使得 恰有四个零点



12.正方体 的棱长为4， 为 的中点， 为 所在平面上一动点，那么以下命题正确的选项是〔    〕

A. 假设 与平面 所成的角为 ，那么点 的轨迹为圆


B. 假设 ，那么 的中点 的轨迹所围成图形的面积为


C. 假设点 到直线 与直线 的距离相等，那么点 的轨迹为抛物线


D. 假设 与 所成的角为 ，那么点 的轨迹为双曲线



三、填空题
13.假设函数 在区间 上的最大值是最小值的 倍，那么 ________.
14.为了贯彻落实习近平总书记在全国教育大会上的讲话精神，2021年中办、国办联合印发了?关于全面加强和改进新时代学校体育工作的意见?，为落实该文件精神，某中学对女生立定跳远工程的考核要求为：1.33米得5分，每增加0.03米，分值增加5分，直到1.84米得90分后每增加0.1米，分值增加5分，总分值为120分，假设某女生训练前的成绩为70分，经过一段时间的训练后，成绩为105分那么该女生经过训练后跳远增加了________米.
15.函数 〔 〕，假设对任意 ， ， ，总有 ， ， 为某一个三角形的边长，那么实数 的取值范围是________.
16. ， 分别为双曲线 : 的左、右焦点， 为双曲线 的右顶点，过 的直线与双曲线 的右支交于 ， ，两点〔其中点 在第一象限〕，设 ， 分别为 ， 的内心，那么 的取值范围是________.
四、解答题
17.在 中 ， ， 分别为内角 ， ， 所对的边，假设 .
〔1〕求 的大小；
〔2〕求 的最大值.
18.在①数列 满足： ， ②等比数列 中，公比 ，前5项和为62，这两个条件中任选一个，并解答以下问题.
〔1〕求数列 的通项公式；
〔2〕设 数列 的前 项和为 ，假设 对 恒成立，求正整数 的最大值.
19.如图，菱形 的对角线 与 交于点 ， ， ，将 沿 折到 的位置使得 ．

〔1〕证明： ．
〔2〕求平面 与平面 所成锐二面角的余弦值．
20.为加强进口冷链食品监管，某省于2021年底在全省建立进口冷链食品集中监管专仓制度，在口岸、目的地市或县〔区、市〕等进口冷链食品第一入境点，设立进口冷链食品集中监管专仓，集中开展核酸检测和预防性全面消毒工作，为了进一步确定某批进口冷冻食品是否感染病毒，在入关检疫时需要对其采样进行化验，假设结果呈阳性，那么有该病毒；假设结果呈阴性，那么没有该病毒，对于 ，〔 〕份样本，有以下两种检验方式：一是逐份检验，那么需检验 次：二是混合检验，将 份样本分别取样混合在一起，假设检验结果为阴性，那么这 份全为阴性，因而检验一次就够了；如果检验结果为阳性，为了明确这 份究竟哪些为阳性，就需要对它们再次取样逐份检验，那么 份检验的次数共为 次，假设每份样本没有该病毒的概率为 〔 〕，而且样本之间是否有该病毒是相互独立的.
〔1〕假设 ，求2份样本混合的结果为阳性的概率；
〔2〕假设取得4份样本，考虑以下两种检验方案：方案一：采用混合检验；方案二：平均分成两组，每组2份样本采用混合检验.假设检验次数的期望值越小，那么方案越“优〞，试问方案一、二哪个更“优〞？请说明理由.
21.在平面直角坐标系中， 为坐标原点，动点 到 ， 两点的距离之和为4.
〔1〕试判断动点 的轨迹是什么曲线，并求其轨迹方程 ；
〔2〕直线 : 与圆 : 交于 、 两点，与曲线 交于 、 两点，其中 、 在第一象限. 为原点 到直线 的距离，是否存在实数 ，使得 取得最大值，假设存在，求出 ；不存在，说明理由.
22.函数 ， .
〔1〕当 时，求 的值域；
〔2〕令 ，当 时， 恒成立，求 的取值范围.

答案解析局部
一、单项选择题
1.【解析】【解答】 表示的点为 ，
因为 ，所以点 位于第四象限，
故答案为：D.

【分析】 先利用复数的乘法运算求出z的代数形式，然后由复数的几何意义求出对应的点的坐标，即可得到答案．
2.【解析】【解答】 集合 ，
，
．
故答案为：A

【分析】先求出集合A,B，再根据交集的定义求出   。
3.【解析】【解答】甲和另一个人一起分到A班有 =6种分法，甲一个人分到 A班的方法有： =6种分法，共有12种分法；
故答案为：B.

【分析】根据排列组合的综合问题代入数值计算出结果即可。
4.【解析】【解答】由题意，12块正方形模板组成以2厘米为首项，最大边长24厘米的等差数列，
所以公差 ，
故第6块正方形模板边长为 厘米，即 6指的板长度为12厘米.
因为眼睛到木板距离为72厘米，
故在直角三角中 ，
所以 ，
故答案为：B

【分析】 由等差数列的通项公式求出六指的高度，再计算tanα和sin2α的值．
5.【解析】【解答】由 ，即 ，得 ，所以 ，
因为点 在椭圆 上，所以 〔 ， 〕，
所以 ，
当且仅当 时，等号成立.
故答案为：C

【分析】 由函数图象恒过定点A，可以确定点A的坐标，进而点A的坐标满足椭圆方程，得到一个等式，再利用根本不等式即可得到结果．
6.【解析】【解答】如下列图，记 为圆上的三个四等分圆周的点，由题意可知：圆是逆时针滚动的，

因为圆的周长为 ，所以 ，且圆上点的纵坐标最大值为2，
当圆逆时针滚动 单位长度时，此时 的相对位置互换，所以 的纵坐标为2，排除BCD，
故答案为：A.

【分析】分析当单位圆向x轴正向滚动个单位长度时A的纵坐标，由此判断出A点形成的轨迹。
7.【解析】【解答】 的图象向左平移 个单位，得到函数 ，
， ，所以 是偶函数，A不正确；
的周期为 ， B不正确；
的图象对称中心为 ，所以关于点 对称，C符合题意；
对称轴为 ，直线 不是 的图象的对称轴，D不正确；
故答案为：C.

【分析】 利用函数y=Asin〔ωx+φ〕的图象变换可得 ，利用余弦函数的性质逐个判断即可得到答案．
8.【解析】【解答】如以下列图所示，取 的中点 ，连接 ，取 的 ，连接 ，取 的中点 ，连接 、 ，

， 为 的中点，那么 ，
平面 ， 平面 ， ，
， 平面 ，
、 分别为 、 的中点，那么 且 ， 平面 ，
平面 ，所以，平面 平面 ，
所以，平面 即为平面 ，设平面 交 于点 ，
在直棱柱 中， 且 ，
所以，四边形 为平行四边形， 且 ，
、 分别为 、 的中点， 且 ，
所以，四边形 为平行四边形， 且 ，
且 ， 且 ，所以，四边形 为平行四边形，
， 平面 ， 平面 ， 平面 ，
设平面 平面 ， 平面 ，所以， ， ，
，所以，四边形 为平行四边形，可得 ，
所以， 为 的中点，
延长 交 于点 ， ，所以， ， ，
又 ，所以， ， ， 为 的中点，
因为平面 平面 ，平面 平面 ，平面 平面 ， ，
， ， ， ， 为 的中点，
， ，那么 ，
为 的中点， ，那么 ，同理 ，
因为直棱柱 的棱长为 ， 为 的中点， ，
由勾股定理可得 ，同理可得 ，
且 ， 平面 ， 平面 ，
平面 ， ，
、 分别为 、 的中点，那么 ， ，
由勾股定理可得 ，同理 .
因此，截面的周长为 .
故答案为：C.

【分析】 结合面面垂直的判定定理和线面垂直的判定定理和性质定理，以及三角形的中位线定理，作出平面，运用勾股定理，计算可得所求值.
二、多项选择题
9.【解析】【解答】对于A，由图可知，这10天中第1日、第3日、第4日的PM2.5日均值小于 ，空气质量为一级，A符合题意；
对于B，由图可知，从6日到9日PM2.5日均值分别为 ， ， ， ，逐渐降低，B符合题意；
对于C，将10天中PM2.5日均值按从小到大排序为： ，
根据中位数的定义可得这10天中PM2.5日均值的中位数是 ，C不符合题意；
对于D，这10天中PM2.5日均值的平均值是 ，D不符合题意.
故答案为：AB

【分析】 由折线图逐一分析数据，找出特例可判断，找出结果．
10.【解析】【解答】由 可得 ，同理可得 ，
因为 时，恒有
所以 ，即 ，A不符合题意B符合题意；
因为 ，
所以 ，即 ，
由不等式性质可得 ，即 ，C符合题意D不符合题意.
故答案为：BC

【分析】根据对数函数的性质，可判断AB正误；由不等式的根本性质可判断CD正误。
11.【解析】【解答】由 可知函数 的图象关于直线 对称.
令 ，即 ，作出函数 的图象如以下列图所示：

令 ，那么函数 的零点个数为函数 、 的图象的交点个数，
的定义域为 ，且 ，那么函数 为偶函数，
且函数 的图象恒过定点 ，
当函数 的图象过点 时，有 ，解得 .
过点 作函数 的图象的切线，
设切点为 ，对函数 求导得 ，
所以，函数 的图象在点 处的切线方程为 ，
切线过点 ，所以， ，解得 ，那么切线斜率为 ，
即当 时，函数 的图象与函数 的图象相切.
假设函数 恰有两个零点，由图可得 或 ，A选项正确；
假设函数 恰有三个零点，由图可得 ，B选项正确；
假设函数 恰有四个零点，由图可得 ，C选项正确，D选项错误.
故答案为：ABC.

【分析】 由   对任意 都成立，推出函数 的图象关于直线 对称，作出函数的图像，令 问题可转化为函数 的零点个数为函数 、 的图象的交点个数，逐一判断即可得出答案.
12.【解析】【解答】如图：

对于A，根据正方体的性质可知， 平面 ，所以 为 与平面 所成的角，
所以 ，所以 ，所以点 的轨迹为以 为圆心， 为半径的圆；A符合题意；
对于B，在直角三角形 中， ，取 的中点 ，因为 为 的中点，所以 ，且 ，因为 ，所以 ，即点 在过点 且与 垂直的平面内，又 ，所以点 的轨迹为以 为半径的圆，其面积为 ，B不正确；
对于C，连接 ，因为 平面 ，所以 ，所以点 到直线 的距离为 ，所以点 到点 的距离等于点 到定直线 的距离，又 不在直线 上，所以点 的轨迹为以 为焦点， 为准线的抛物线，C符合题意；
对于D，以 为原点， 分别为 轴建立空间直角坐标系，
那么 ， ， ，设 ，
那么 ， ，
因为 与 所成的角为 ，所以 ，
所以 ，整理得 ，所以点 的轨迹为双曲线，D符合题意.
故答案为：ACD

【分析】 对于A,根据正方体的性质计算出DN=2，根据圆的定义可得答案；
对于B，取MD的中点E，根据，， 可得点 的轨迹为以 为半径的圆，根据圆的面积公式计算可得结果；
对于C，将点N到直线 的距离为 ， 再根据抛物线的定义可得结果；
对于D，建立空间直角坐标系，利用向量的夹角公式列式可解得结果。
三、填空题
13.【解析】【解答】 ，所以，函数 在区间 上为增函数，
由条件可得 ， ， ，解得 .
故答案为： .

【分析】 判断函数的单调性，求解函数的最值，列出关系式求解a即可．
14.【解析】【解答】该生成绩为70分时，其立定跳远距离为 米，
该生成绩为105分时，其立定跳远距离为 米，
所以增加了 米，


【分析】 根据先求出训练前的跳远距离，再求出训练后的跳远距离，由此即可求解．
15.【解析】【解答】由题意可得：对 ， ， ，总有 恒成立，
只需
，
①当 时， ，满足题意；
②当 时， 在 上单调递减， ，故需 ，即 ；
综上所述， 的取值范围是[3,6]．
故答案为：[3,6]

【分析】   ， 由a≥3，可得f〔x〕的单调性，进而求得函数的值域，问题转化为，对， ， ，恒成立求解即可．
16.【解析】【解答】如图：

设 的内切圆与 分别切于 ，
所以 ，
所以 ，
又 ，所以 ，
又 ，所以 与 重合，所以 的横坐标为 ，同理可得 的横坐标也为 ，
设直线 的倾斜角为 .那么 ， ，



，
当 时， ，
当 时，由题知， . . .
因为 两点在双曲线的右支上，∴ ，且 ，所以 或 ，
∴ .且 ， ，
综上所述， .
故答案为：

【分析】 根据圆的切线长定理和双曲线的定义可推得   ， 内切圆与x轴切于双曲线的右顶点E，设直线 的倾斜角为 ， 可用表示 ， 根据A,B两点都在右支上得到的范围，利用的范围可求得的取值范围。
四、解答题
17.【解析】【分析】 〔1〕由正弦定理化简等式可得 ，由余弦定理可得cosA的值，结合A∈〔0，π〕，可得A的值．
〔2〕由〔1〕利用三角函数恒等变换的应用可得 ，利用正弦函数的性质可求其最大值．
 
 
18.【解析】【分析】 〔1〕分别选①②，运用等比数列的定义和通项公式、求和公式，解方程可得首项和公比，即可得到所求通项公式；
〔2〕求得 ，由数列的错位相减法求和，结合等比数列的求和公式，计算可得Tn ， 判断{Tn}的单调性，求得最小值，解不等式可得所求m的最大值．
 
 
19.【解析】【分析】 〔1〕证明AC⊥BD，推出BE⊥AC，PE⊥AC．然后证明AC⊥平面PBE．即可证明PB⊥AC；
〔2〕取DE的中点O，连接OP，取CD的中点F，连接OF．以O为坐标原点，  ，  ， 的方向分别为x，y，z轴的正方向，建立如下列图的空间直角坐标系O-xyz．求出平面PAB的法向量，平面PCD的法向量利用空间向量的数量积求解二面角的余弦函数值即可．
 
 
20.【解析】【分析】 〔1〕先求出该混合样本阴性的概率，根据对立事件可得阳性的概率；
〔2〕方案一：混在一起检验，方案一的检验次数记为X，那么X的可能取值为1，5，分别求出P〔X=1〕，P〔X=5〕，由此能求出X的分布列和E〔X〕；方案二：由题意分析得每组2份样本混合检验时，假设阴性那么检验次数为1，概率为   ，假设阳性，那么检测次数为3，概率为1-p，方案二的检验次数记为Y，那么Y的可能取值为2，4，6，分别求出相应的概率，从而求出Y的分布列和E〔Y〕，由此能求出结果．
 
 
21.【解析】【分析】〔1〕根据椭圆的定义可得方程；
〔2〕分析可知 ，再代入消元，用韦达定理及弦长公式得到T的函数关系式，再求最值。
 
 
22.【解析】【分析】 〔1〕求出   ，利用导数判断函数  的单调性，从而求出  的最值，即可得到  的值域；
〔2〕当  时，  ， 将不等式   进行变形，最终化为  对   恒成立， 令 ，然后利用导数研究函数  的单调性，结合〔1〕中的结论可推导出即   ，从而得到   即可求出 的取值范围.