2021届北京市西城区高三数学一模试卷及答案

这是一份2021届北京市西城区高三数学一模试卷及答案，共12页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
 高三数学一模试卷
一、单项选择题
1.集合 ， ，那么 〔    〕
A. {2}                                 B.                                  C.                                  D. 



z满足 ，那么z的虚部是〔    〕
A. -1                                          B. 1                                          C.                                           D. i



3.在 的展开式中，常数项为〔    〕
A. 15                                        B. -15                                        C. 30                                        D. -30



4.某四棱锥的三视图如下列图，那么该四棱锥的外表积为〔    〕

A. 12                                    B.                                     C. 16                                    D. 



5.函数 ，那么不等式 的解集是〔    〕
A.                                 B.                                 C.                                 D. 



6.在 中， ，点P是 的中点，那么 〔    〕
A.                                            B. 4                                           C.                                            D. 6



7.在 中， ，那么 〔    〕
A.                                         B.                                         C. 6                                        D. 5



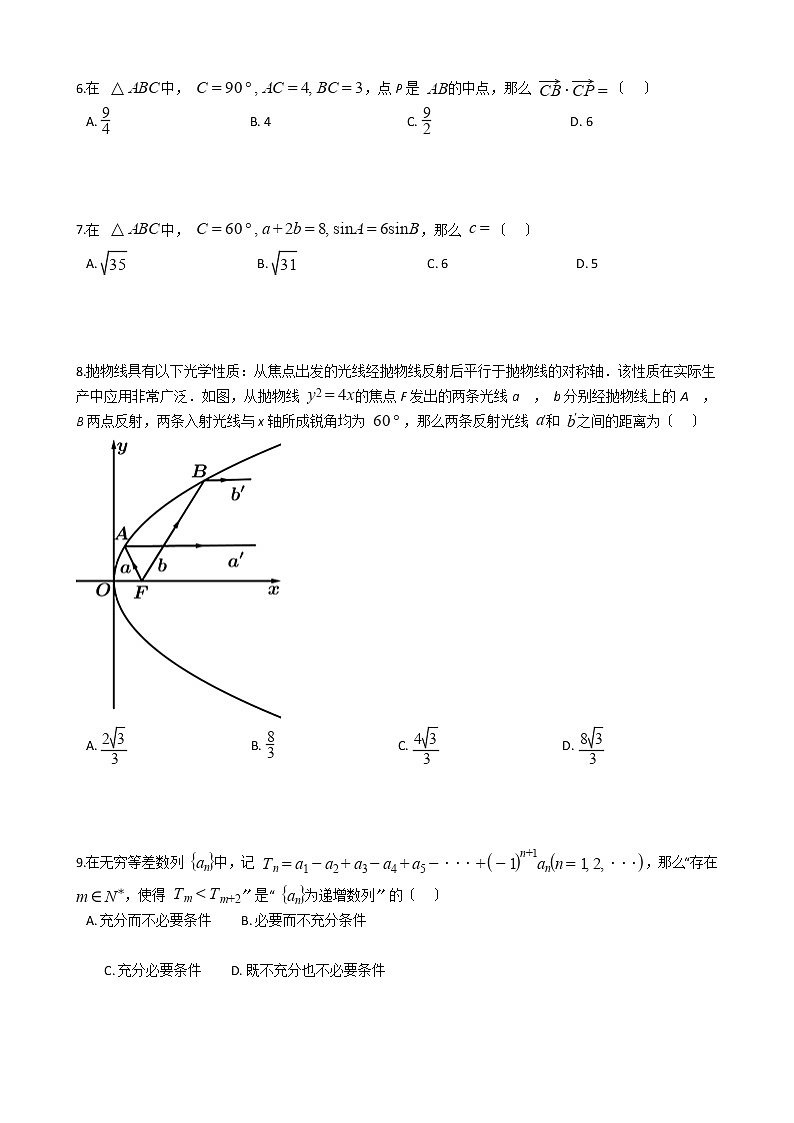
8.抛物线具有以下光学性质：从焦点出发的光线经抛物线反射后平行于抛物线的对称轴．该性质在实际生产中应用非常广泛．如图，从抛物线 的焦点F发出的两条光线a ， b分别经抛物线上的A ， B两点反射，两条入射光线与x轴所成锐角均为 ，那么两条反射光线 和 之间的距离为〔    〕

A.                                      B.                                      C.                                      D. 



9.在无穷等差数列 中，记 ，那么“存在 ，使得 〞是“ 为递增数列〞的〔    〕
A. 充分而不必要条件         B. 必要而不充分条件

         C. 充分必要条件         D. 既不充分也不必要条件



X中存在最大元素M和最小元素m ， 那么记 ．以下命题中正确的选项是〔    〕
A.  ， ，且 ，那么


B.  ， ，那么存在实数a ， 使得


C.  ，假设 ，那么对任意 ，都有


D.  ， ，那么对任意的实数a ， 总存在实数b ， 使得



二、填空题
11.函数f〔x〕=lnx+ 的定义域为________．
12.函数 ，假设对任意 都有 〔c为常数〕，那么常数m的一个取值为________．
13.长江流域水库群的修建和联合调度，极大地降低了洪涝灾害风险，发挥了重要的防洪减灾效益．每年洪水来临之际，为保证防洪需要、降低防洪风险，水利部门需要在原有蓄水量的根底上联合调度，统一蓄水，用蓄满指数〔蓄满指数=〔水库实际蓄水量〕÷〔水库总蓄水量〕×100〕来衡量每座水库的水位情况．假设某次联合调度要求如下：
〔ⅰ〕调度后每座水库的蓄满指数仍属于区间 ；
〔ⅱ〕调度后每座水库的蓄满指数都不能降低；
〔ⅲ〕调度前后，各水库之间的蓄满指数排名不变．
记x为调度前某水库的蓄满指数，y为调度后该水库的蓄满指数，给出下面四个y关于x的函数解析式：
① ；② ；③ ；④ ．
那么满足此次联合调度要求的函数解析式的序号是________．
14.双曲线 ，那么C的渐近线方程是________；过C的左焦点且与x轴垂直的直线交其渐近线于M ， N两点，O为坐标原点，那么 的面积是________．
15.在等比数列 中， ，那么公比 ________；假设 ，那么n的最大值为________．
三、解答题
16.如图，在正方体 中，E为 的中点．

〔1〕求证： 平面 ；
〔2〕求直线 与平面 所成角的正弦值．
17.函数 ，且 图象的相邻两条对称轴之间的距离为 ，再从条件①、条件②、条件③中选择两个作为一组条件．
〔1〕确定 的解析式；
〔2〕假设 图象的对称轴只有一条落在区间 上，求a的取值范围．
条件①： 的最小值为 ；
条件②： 图象的一个对称中心为 ；
条件③； 的图象经过点 ．
18.天文学上用星等表示星体亮度，星等的数值越小，星体越亮．视星等是指观测者用肉眼所看到的星体亮度；绝对星等是假定把恒星放在距地球32.6光年的地方测得的恒星的亮度，反映恒星的真实发光本领．下表列出了〔除太阳外〕视星等数值最小的10颗最亮恒星的相关数据，其中 ．
星名
天狼星
老人星
南门二
大角星
织女一
五车二
参宿七
南河三
水委一
参宿四
视星等









a
绝时星等










赤纬










〔1〕从表中随机选择一颗恒星，求它的绝对星等的数值小于视星等的数值的概率；
〔2〕北京的纬度是北纬 ，当且仅当一颗恒星的“赤纬〞数值大于 时，能在北京的夜空中看到它．现从这10颗恒星中随机选择4颗，记其中能在北京的夜空中看到的数量为 颗，求 的分布列和数学期望；
〔3〕记 时10颗恒星的视星等的方差为 ，记 时10颗恒星的视星等的方差为 ，判断 与 之间的大小关系．〔结论不需要证明〕
19.函数 ．
〔1〕假设 ，求曲线 在点 处的切线方程；
〔2〕假设 ，求证：函数 存在极小值；
〔3〕假设对任意的实数 ， 恒成立，求实数a的取值范围．
20.椭圆 的焦点在x轴上，且经过点 ，左顶点为D ， 右焦点为F ．
〔1〕求椭圆C的离心率和 的面积；
〔2〕直线 与椭圆C交于A ， B两点，过点B作直线 的垂线，垂足为G ， 判断是否存在常数t ， 使得直线 经过y轴上的定点？假设存在，求t的值；假设不存在，请说明理由．
A： 的各项均为正整数，设集合 ，记T的元素个数为 ．
〔1〕假设数列A：1，2，4，3，求集合T ， 井写出 的值；
〔2〕假设A是递增数列，求证：“ 〞的充要条件是“A为等差数列〞；
〔3〕假设 ，数列A由 这 个数组成，且这 个数在数列A中每个至少出现一次，求 的取值个数．

答案解析局部
一、单项选择题
1.【解析】【解答】解：因为 ，
所以
故答案为：A

【分析】根据题意由交集的定义即可得出答案。
2.【解析】【解答】设 ，
因为 ，可得 ，
那么 ，可得 ，所以复数 的虚部是-1.
故答案为：A

【分析】根据题意由共轭复数的定义整理化简再由复数的定义即可得出答案。
3.【解析】【解答】 ，
令 ，得 ，
所以常数项是 .
故答案为：A

【分析】根据题意首先求出二项展开式的通项公式，再由条件令 ，得 ， 代入数值计算出结果即可。
4.【解析】【解答】解：根据几何体的三视图得到直观图，如以下列图所示四棱锥 ：那么 ，所以

所以外表积为
．
故答案为：D．

【分析】根据题意由三视图的定义即可得出该几何体为四棱锥结合外表积的公式代入数值计算出结果即可。
5.【解析】【解答】 的定义域为 ，由
所以 在 上递减，又 ，
所以不等式 的解集是 ．
故答案为：D

【分析】根据题意首先求出函数的定义域再对其求导结合导函数的性质即可得出函数f(x)的单调性，再由单调性的性质即可得出不等式的解集。
6.【解析】【解答】解：如图建立平面直角坐标系，那么 ， ， ，

所以 ， ，所以
故答案为：C

【分析】 利用向量的数量积以及向量的线性运算即可求解．
7.【解析】【解答】解：因为 ，由正弦定理可得 ，又 ，所以 ， ，
因为
所以 ，即 ，解得 ，
故答案为：B

【分析】根据题意即可得出， 再由正弦定理计算出a与b的值，再把数值代入到余弦定理计算出c的值即可。
8.【解析】【解答】解：由 得 ， ，所以 ，即 ； 消去 得 ，所以 ，或 〔舍去〕，即 ；
同理 即 ； 消去 得 ，所以 ，或 〔舍去〕，即 ；
所以 ，即两条反射光线 和 之间的距离为
故答案为：C

【分析】 由抛物线的方程得F〔1，0〕，又∠OFA=60°，写出直线AF的方程，并联立抛物线的方程，解得yA ， 同理解得yB ， 再计算|yA-yB|即可得出答案．
9.【解析】【解答】假设存在 ，使得 ，
那么 ，
当 为奇数时，只需 ，即 ；
当 为偶数时，只需 ，即 ；
即此时只能判断 与 的大小关系，无法得到 为递增数列，充分性不成立；
当 为递增数列时， ，
只需 ，即 为奇数，即可满足 ，必要性成立；
“存在 ，使得 〞是“ 为递增数列〞的必要不充分条件.
故答案为：B.

【分析】根据等差数列的性质以及充分和必要条件的定义即可得出答案。
10.【解析】【解答】对于A：由 ，那么 ； ，那么 ，解得： ，A不符合题意；
对于B：由 ，那么 ；
，那么 ，
①当 时， 在 上单减，所以 ，解得： ，又 ，所以a不存在；
②当 时， 在 上单减，在 上单增，且 所以 ，解得： ，又 ，所以a不存在；
③当 时， 在 上单减，在 上单增，且 所以 ，解得： ，又 ，所以a不存在；
④当 时， 在 上单增，所以 ，解得： ，又 ，所以a不存在；
综上所述：不存在实数a ， 使得 .
B不符合题意；
对于C：∵ ，而 ，那么M=1,N=-1,但对任意 ，都有 ，不一定成立；
对于D：∵ ，∴ ，由 得 ，所以那么对任意的实数a ， 总存在实数b ， 使得 ，D成立.
故答案为：D

【分析】根据题意对选项 A举反例判断；选项B用反证法，分类讨论判断；选项C举反例判断； 选项D对任意的实数a，求出b满足条件即可．
二、填空题
11.【解析】【解答】解：∵函数f〔x〕=lnx+ ， ∴ ，
解得0＜x≤1；
∴函数f〔x〕的定义域为{x|0＜x≤1}．
故答案为：{x|0＜x≤1}．
【分析】根据函数f〔x〕的解析式，列出使解析式有意义的不等式组，从而求出f〔x〕的定义域．
12.【解析】【解答】函数 中心对称点都在x轴上，所以 ，
所以 对任意 恒成立，
，
所以 ，故利用诱导公式得 都可满足条件.
故答案为：π〔答案不唯一，只要是〔2k+1〕π即可〕

【分析】首先由三角函数的恒等变形，要使对任意 恒成立，即可得出即， 由诱导公式计算出结果即可。
13.【解析】【解答】① ，该函数在 时函数值为 ，超过了范围，不合题意；
② 为增函数，且
且 ，那么 ，符合题意；
③ ，当 时 ，不合题意
④ ，当 时， ，故该函数在 上单调递增，又
设

即 ，
易知 在 上为减函数
令 ，那么存在 ，有
当 ， ；当 ， ；
故 在 递增，在 递减.
，
故 上
即 上
故④符合题意
故答案为：②④

【分析】 根据题意得到，y的定义域为[0，100]，值域为[0，100]，y≥x对任意的x∈[0，100]成立且在[0，100]上单调递增，由此对四个选项进行逐一的分析判断即可．
14.【解析】【解答】解：因为双曲线 ，所以 ， ，所以 ，即 ，所以渐近线方程为 ，焦点坐标为 与 ，
当 时 ，即 ，所以
故答案为： ， ；

【分析】 利用双曲线的标准方程，求解渐近线方程得到第一空；求出M坐标，然后求解三角形的面积解答第二空．
15.【解析】【解答】解：因为 ，所以 ，所以 ，即 ，所以 ；所以当 为偶数时， ，当 为奇数时，
要使 ，所以 且 为奇数即 且 为奇数，所以 或
故答案为： ，3

【分析】 根据题意，由等比数列的通项公式可得， 即可得出答案，进而求出a1的值，即可得{an}的通项公式，解an＞1即可得出答案．
三、解答题
16.【解析】【分析】 〔1〕根据题意要证BD1∥平面EAC，只需在平面EAC内找一条直线BD1与平行，根据中位线定理可知EF∥D1B，满足线面平行的判定定理所需条件，即可得到结论；
〔2〕连结OB1 ， EB1 ， 由勾股定理得出OB1⊥OE，由AB1=B1C得出OB1⊥AC，于是OB1⊥平面ACE，从而平面EAC⊥平面AB1C；
 
 
17.【解析】【分析】(1)根据题意由函数f(x)的图象即可得出周期的值，再由周期的公式代入数值计算出的值，由此得出函数的解析式选条件①②，首先求出A的值，再由函数的图象把点的再把代入函数的解析式计算出， 由此得到函数的解析式。 选条件①③，把点的再把代入函数的解析式计算出 进而得出函数的解析式。 选条件②③，把点的坐标代入到函数的解析式求出A的值，再把点代入到函数的解析式求出即可。
(2)根据题意由函数的图象的性质结合正弦函数的单调性即可得出， 由此得出a的取值范围。
 
18.【解析】【分析】 (1)由图表中的数据可知有5颗恒星绝对星等的数值小于视星等的数值，由古典概型的概率公式求解即可；
(2)首先确定X的所有可能取值，利用超几何分布的概率公式计算得到每个取值对应的概率，列出分布列，由数学期望的计算公式求解期望即可；
(3)根据数据的波动程度可得方差的大小关系．
 
 
19.【解析】【分析】 〔1〕根据题意首先求出函数的导数，再计算f′〔1〕，f〔1〕的值，代入切线方程即可；
〔2〕根据题意首先求出函数的导数，通过讨论a的范围，确定函数的单调区间，表示出最小值，得到关于a的方程，判断a的具体范围即可．
 
 
20.【解析】【分析】(1)根据题意由点在椭圆上把点的坐标代入到椭圆的方程计算出a的值，再结合椭圆的 a、b 、c 三者的关系计算出c的值，从而求出离心率的值，再把数值代入三角形的面积公式计算出结果即可。
(2)首先根据两种特殊情况求出定点〔0，2〕，从而计算出t的值再证明实数t=3时，使得直线AG经过y轴上的定点〔0，2〕。
 
 
21.【解析】【分析】 (1)利用集合T的定义直接求解即可；
(2)分充分性和必要性两个方面分别证明，利用题中给出的集合T的定义分析即可；
(3)通过分析可知P〔T〕≤4n-1，且P〔T〕≥2n，设数列A0：1，1，2，2，3，3，4，4，…，n，n，2n，此时T={0，1，2，…，2n-1}，P〔T〕=2n．然后对数列A0分别作变换进行分析求解，即可得到答案．