2021届安徽省马鞍山市高三上学期文数第一次教学质量监测试卷及答案

这是一份2021届安徽省马鞍山市高三上学期文数第一次教学质量监测试卷及答案，共13页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

 高三上学期文数第一次教学质量监测试卷
一、单项选择题
1.集合 ，那么A∩B=〔    〕
A. {2，3，4}                      B. {2，3，4，5}                      C.                       D. {x|2 2.假设复数 满足 (其中 为虚数单位)那么复数 的虚部为〔    〕
A.                                       B.                                       C.                                       D. 
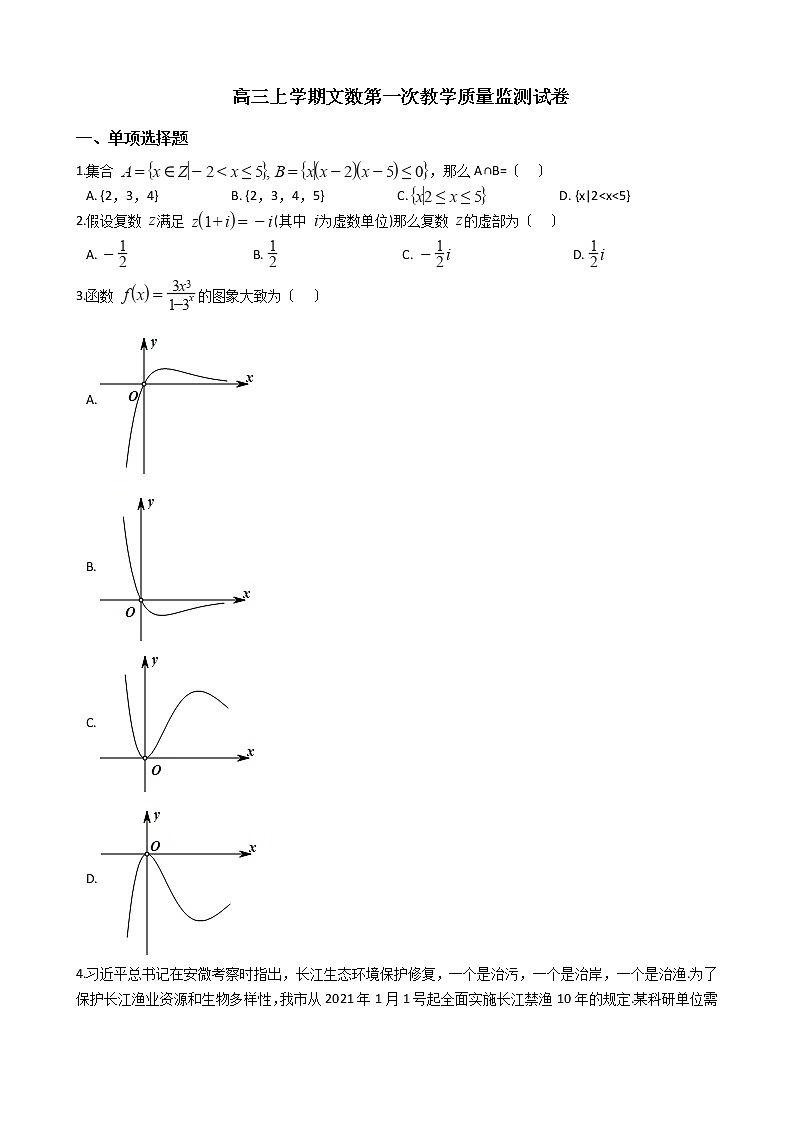
3.函数 的图象大致为〔    〕
A. 
B. 
C. 
D. 
4.习近平总书记在安微考察时指出，长江生态环境保护修复，一个是治污，一个是治岸，一个是治渔.为了保护长江渔业资源和生物多样性，我市从2021年1月1号起全面实施长江禁渔10年的规定.某科研单位需要从长江中临灭绝的白豚、长江江豚、达氏鲟、白鲟、中华鲟这5种鱼中随机选出3种进行调查研究，那么白鲟和中华鲟同时被选中的概率是〔    〕
A.                                          B.                                          C.                                          D. 
5.平面向量 与 的夹角为 ，假设 ，那么 〔    〕
A.                                           B. 2                                          C. 3                                          D. 4
6.执行如以下图的程序框图，那么输出的s=〔    〕

A.                       B.                       C.                       D. 
7.如图，在正方体 中， ， ， 分别为棱 ， ， 的中点，那么 与 所成角的余弦值为〔    〕

A.                                      B.                                      C.                                      D. 
8.将函数f(x)=sin2x-cos2x的图象向左平移 个单位长度，所得图象对应的函数〔   〕
A. 在区间[0， ]上单调递增                                 B. 最小正周期为
C. 图象关于 对称                                          D. 图象关于( ，0)对称
9.己知直线 过抛物线y2=4x的焦点F，并与抛物线交于A，B两点，假设点A的纵坐标为4，那么线段AB的长为〔    〕
A.                                        B.                                        C.                                        D. 
10.函数 的图象在(1，f〔1〕)处的切线经过坐标原点，那么函数y=f(x)的最小值为〔    〕
A.                                B.                                C.                                D. 1
1 ， F2分别是双曲线 的左、右焦点，过F2作双曲线的一条渐近线的垂线，垂足为H，假设|HF1|=3|HF2|，那么双曲线的离心率为〔   〕
A.                                       B.                                       C.                                       D. 
12.数列{an}满足 ，且a1=1，a2=5，那么 〔    〕
A. 69                                       B. 105                                       C. 204                                       D. 205
二、填空题
13.某班级为了解本班49名学生的体质健康状况，将这些学生编号为1，2，3，…，49，从这些学生中用系统抽样方法等距抽取7名学生进行体质健康测试.假设32号学生被抽到，那么在8-14号学生中被抽到的是________号.
14.设实数 、 满足约束条件 ，那么 的最大值为________.
15.等比数列{an}的前n项和为Sn ， 且 ，那么实数 的值为________
16.如图，在三棱锥 中， 平面 ， ， ， ， 是 的中点，那么过点 的平面截三棱锥 的外接球所得截面的面积最小值为________

三、解答题
17.天气寒冷，加热手套比较畅销，某商家为了解某种加热手套如何定价可以获得最大利润，现对这种加热手套进行试销售，统计后得到其单价x(单位;元)与销量y(单位:副)的相关数据如下表：
单价x〔元〕
80
85
90
95
100
销量y〔副〕
140
130
110
90
80
附:对于一组数据(x1 ， y1)，(x2 ， y2)，…，(xn ， yn)，其回归直线 的斜率和截距的最小二乘估计分别为
参考数据:
〔1〕销量y与单价x具有线性相关关系，求y关于x的线性回归方程;
〔2〕假设每副该加热手套的本钱为65元，试销售结束后，请利用〔1〕中所求的线性回归方程确定单价为多少元时，销售利润最大?(结果保存到整数)
18.在 中，角 ， ， 所对的边分别是 ， ， ，且 .
〔1〕假设 ，求角 的大小；
〔2〕假设 ， ，求 的面积.
19.如图，BE，CD为圆柱的母线， 是底面圆的内接正三角形，M为BC的中点.

〔1〕证明：平面AEM⊥平面BCDE；
〔2〕设BC=BE，圆柱的体积为 ，求四棱锥A-BCDE的体积.
20.点 在圆 上， ， ，线段 的垂直平分线与 相交于点 .
〔1〕求动点 的轨迹方程;
〔2〕假设过点 的直线 斜率存在，且直线 与动点 的轨迹相交于 ， 两点.证明：直线 与 的斜率之积为定值.
21. 是自然对数的底数，函数 ，其中 .
〔1〕当 时，假设 ，求 的单调区间;
〔2〕假设 在 上恰有三个零点，求 的取值范围.
22.平面直角坐标系xOy中，曲线 的参数方程为 (t为参数)，以坐标原点O为极点，x轴非负半轴为极轴建立极坐标系，曲线 的极坐标方程为
〔1〕求曲线 的普通方程与 的直角坐标方程;
〔2〕求 上的动点到 距离的取值范围.
23.函数f(x)=2|x-1|+|x+2|.
〔1〕求不等式f(x)≥6的解集;
〔2〕假设 对任意x∈R恒成立，求实数m的取值范围.

答案解析局部
一、单项选择题
1.【解析】【解答】 ，
，
所以A∩B={2，3，4，5}。
故答案为：B

【分析】利用条件结合一元二次不等式求解集的方法，进而求出集合B，再利用集合A中x的取值范围结合元素与集合的关系，进而求出集合A，再结合交集的运算法那么，进而求出集合A和集合B的交集。
2.【解析】【解答】由 可得 ，
所以复数 的虚部为 。
故答案为：A

【分析】利用条件结合复数的乘除法运算法那么，进而求出复数z，再利用复数虚部的定义，进而求出复数z的虚部。
3.【解析】【解答】由 可得 ，所以函数 的定义域为 ，
当 时， ，所以 ， ，可得 ，故排除A、C，
当 时， ，所以 ， ，可得 ，故排除B,
故答案为：D

【分析】利用分式函数求定义域的方法，进而求出函数的定义域，再利用分类讨论的方法结合同号为正、异号为负的性质，进而得出函数值的正负，从而结合排除法找出函数的大致图象。
4.【解析】【解答】5种鱼中随机选出3种的取法： ，
白鲟和中华鲟同时被选中的取法： ，
所以白鲟和中华鲟同时被选中的概率 。
故答案为：B

【分析】利用实际问题的条件结合组合数公式，再结合古典概型求概率公式，进而求出白鲟和中华鲟同时被选中的概率。
5.【解析】【解答】解： ， ，
所以 ，
，且 ， 解得 。
故答案为：C．

【分析】利用条件结合向量的模的坐标表示结合数量积求向量的模的公式，再结合数量积的坐标表示结合数量积的运算法那么，进而求出向量 的模。
6.【解析】【解答】由程序框图可知，
输出的
 
。
故答案为：B。

【分析】利用条件结合程序框图的顺序结构、条件结构和循环结构，进而求出输出的s的值。
7.【解析】【解答】如图以 为原点，分别以 所在的直线为 轴建立空间直角坐标系，

设正方体的棱长为 ，那么 ， ， ， ，
所以 ， ，
设 与 所成的角为 ，
所以 ，
异面直线与 所成角的余弦值为 ，
故答案为：A

【分析】以 为原点，分别以 所在的直线为 轴建立空间直角坐标系，设正方体的棱长为 ，进而求出点的坐标，再利用向量的坐标表示，进而求出向量的坐标，再利用两向量的数量积求向量夹角公式，进而求出异面直线与 所成角的余弦值。
8.【解析】【解答】 ，
其图象向左平移 个单位长度，
可得 ，
当 时， ，所以函数
在区间[0， ]上不单调，A不正确；
最小正周期为 ，B不正确；
当 时， ，即 ，C符合题意、D不正确；
故答案为：C

【分析】利用辅助角公式化简函数为正弦型函数，再利用正弦型函数的图象变换，进而求出变换后的函数解析式，再利用换元法将正弦型函数转化为正弦函数，再利用正弦函数的图像判断出正弦型函数在区间[0， ]上的单调性，再利用正弦型函数的最小正周期公式，进而求出正弦型函数的最小正周期，再利用换元法将正弦型函数转化为正弦函数，再利用正弦函数的图像判断出正弦型函数的对称点和对称轴，进而选出正确的选项。
9.【解析】【解答】 当时， ，即 ，
，设 ，利用 三点共线，可知 ，
化简得 ，解得： 或 〔舍〕，
当 时， ，即 ， ，
所以 。
故答案为：D

【分析】利用抛物线的标准方程确定焦点的位置，进而求出焦点的坐标，再利用点斜式方程设出过抛物线y2=4x的焦点F的直线方程，再利用直线与抛物线交于A，B两点，联立二者方程结合点A的纵坐标为4，进而求出A,B的坐标，再利用抛物线的定义，进而结合抛物线的弦长公式，从而求出线段AB的长。
10.【解析】【解答】函数 ，那么 ，
且 ，所以 ，
所以 ，解得 ，
所以 ，〔 〕，
，
令 ，即 ，解得 ，
令 ，即 ，解得 ，
所以函数在区间 上单调递减，在区间 上单调递增，
所以 。
故答案为：C

【分析】利用求导的方法切成函数在切点处的切线的斜率，再利用切点的横坐标求出切点的纵坐标，进而求出切点的坐标，再利用点斜式求出函数在切点处的切线方程，再利用切线经过坐标原点，结合代入法，进而求出a的值，从而求出函数的解析式，再利用求导的方法判断函数的单调性，再利用函数的单调性求出函数的最小值。
11.【解析】【解答】由题设知双曲线C： 的一条渐近线方程为 ： ，

∵右焦点 ，且 ，
∴ ，
∴ ，由 ，解得 ，
∴ ，∴ ，
平方化简得 ，
又 ，
∴ ，即 ，
，即 ，
所以 ，故得 ，
故答案为：D.

【分析】利用条件结合双曲线标准方程确定焦点的位置，进而结合双曲线中a,b,c三者的关系式，进而求出c的值，从而求出焦点的坐标，再利用焦点的位置求出双曲线的一条渐近线方程，再利用过F2作双曲线的一条渐近线的垂线，垂足为H，再结合两直线垂直斜率之积等于-1，进而求出渐近线的垂线的斜率，再利用点斜式求出渐近线垂线的方程，再利用条件 |HF1|=3|HF2|结合两点距离公式，进而求出a,b的关系式，再利用双曲线中a,b,c三者的关系式，进而求出a,c的关系式，再结合双曲线离心率公式变形，进而求出双曲线的离心率。
12.【解析】【解答】因为 ，所以 ，
故数列 构成以4为首项，1为公差的等差数列，
，
故 …… ……
。
故答案为：D

【分析】因为 ，所以 ， 再利用等差数列的定义推出数列 构成以4为首项，1为公差的等差数列，再利用等差数列的通项公式，进而求出数列 的通项公式，再利用累加法，进而结合等差数列前n项和公式和分组求和的方法，从而求出的值。
二、填空题
13.【解析】【解答】由题意知49名学生用系统抽样方法等距抽取7名学生进行体质健康测试，
间隔 ，
设第一组 号中被抽出的为 号，
第二组 号中被抽出的为 号，
第三组 号中被抽出的为 号，
第四组 号中被抽出的为 号，
第五组 号中被抽出的为 号，
解得： ，
所以第二组 号中被抽出的为 号，
故答案为：11。

【分析】利用条件结合系统抽样的方法，进而得出在8-14号学生中被抽到的号数。
14.【解析】【解答】作出不等式组 所表示的可行域如以下图所示：

联立 ，解得 ，即点 ，
平移直线 ，当该直线经过可行域的顶点 时，直线 在 轴上的截距最大，此时 取最大值，即 。
故答案为：33。

【分析】利用条件结合二元一次不等式组求出可行域，再利用可行域求出最优解，再结合最优解求出线性目标函数的最大值。
15.【解析】【解答】当 时， ，两式相减得 ，
即 ，并且数列 是等比数列，
所以 ，
， ，
当 时， ，
解得 。
故答案为： 。

【分析】利用条件结合与的关系式，再利用分类讨论的方法，进而结合等比数列的定义，从而判断出数列 是等比数列，再利用等比数列的定义，进而求出等比数列的公比，再利用等比数列的通项公式结合条件，进而求出实数 的值 。
16.【解析】【解答】 平面 ， ，将三棱锥 补成长方体 ，

那么三棱锥 的外接球直径为 ，所以， ，
设球心为点 ，那么 为 的中点，连接 ，
、 分别为 、 的中点，那么 ，且 ，设过点 的平面为 ，设球心 到平面 的距离为 .
①当 时， ；
②当 不与平面 垂直时， .
综上所述， ，
设过点 的平面截三棱锥 的外接球所得截面圆的半径为 ，那么 ，
因此，所求截面圆的面积的最小值为 。
故答案为：π。

【分析】因为 平面 ，结合线面垂直的定义证出线线垂直，即 ，将三棱锥 补成长方体 ，再利用勾股定理求出长方体的体对角线，再结合长方体的体对角线等于三棱锥的外接球的直径，进而求出三棱锥外接球的半径，设球心为点 ，那么 为 的中点，连接 ，因为点、 分别为 、 的中点，再利用中点作中位线的的方法结合中位线的性质，进而推出线线平行，那么 ，再利用勾股定理，进而求出OM的长，设过点 的平面为 ，设球心 到平面 的距离为 ，①当 时， ；②当 不与平面 垂直时， ，进而求出， 设过点 的平面截三棱锥 的外接球所得截面圆的半径为 ，再利用勾股定理，进而求出r的值，再结合圆的面积公式，进而求出过点 的平面截三棱锥 的外接球所得截面的面积最小值。
 
三、解答题
17.【解析】【分析】〔1〕 由表中数据结合最小二乘法的方法，进而求出 y关于x的线性回归方程 。
〔2〕 设定价为 元，利润为 ， 再利用实际问题的条件，进而得出利润为二次函数，再利用二次函数图象求最值的方法，进而结合 〔1〕中所求的线性回归方程确定单价为95元时的销售利润最大。
18.【解析】【分析】〔1〕利用条件结合正弦定理，再利用三角形中角B,C的取值范围，进而求出角B的余弦值，再结合三角形中角B的取值范围，进而求出角B的值，再利用二倍角的余弦公式结合一元二次方程求出角A的余弦值，再利用三角形中角A的取值范围，进而求出角A的值。
〔2〕 由〔1〕知， ，又 ， ， 再利用余弦定理，进而求出c的值，再利用分类讨论的方法结合三角形面积公式，进而求出三角形 的面积 。
19.【解析】【分析】〔1〕利用题意可得 ，又因为 为圆柱的母线，所以结合线线垂直证出线面垂直，即 平面 ，再利用线面垂直的定义证出线线垂直，即 ， 再利用线线垂直证出线面垂直，即 平面 ，再利用线面垂直证出面面垂直，即证出平面AEM⊥平面BCDE。
〔2〕 由题可设 ，由 是底面圆的内接正三角形易得，底面圆的半径 ，再利用圆柱的体积公式结合条件，进而求出t的值，再由〔1〕可知， 平面 ，再利用四棱锥的体积公式，进而求出四棱锥A-BCDE的体积。

 
20.【解析】【分析】〔1〕利用圆的标准方程求出圆心坐标和半径长，因为点 在线段 的垂直平分线上，所以，那么，再由椭圆的定义可得
动点 的轨迹是以 ， 为焦点，长轴长为 的椭圆，进而求出a,c的值，再结合椭圆中a,b,c三者的关系式，进而求出b的值，从而求出椭圆的标准方程。
〔2〕设直线的斜截式方程为 ， 再利用直线 与动点 的轨迹相交于 ， 两点，联立二者方程结合判别式法和韦达定理，再结合两点求斜率公式，进而化简证出直线 与 的斜率之积为定值。

 
21.【解析】【分析】〔1〕利用a的值求出函数的解析式，再利用求导的方法求出函数f(x〕的导函数，再利用 ， 进而求出函数g(x)的解析式，再利用求导的方法判断函数的单调性，进而求出求出函数g(x)的单调区间。
〔2〕利用条件结合函数的零点与方程的根的等价关系，得出假设 在 上恰有三个零点等价于 有三个不等的实根，等价于方程 有三个不等的实根，设 ，那么 与 两个函数图象有三个不同的交点结合求导的方法判断函数的单调性，再利用函数的单调性画出函数h(x)的图象和直线y=a的图像，再结合二者的图像和条件，进而求出实数a的取值范围。
 
22.【解析】【分析】〔1〕利用条件结合参数方程与普通方程的转化方法，再结合极坐标与直角坐标的互化公式，进而求出曲线 的普通方程与 的直角坐标方程。
〔2〕 曲线 的参数方程为 〔 为参数〕，设 上的动点为 ， 再利用两点距离公式结合辅助角公式化简曲线 上的动点到曲线 的距离为正弦型函数，再利用正弦型函数的图像求出正弦型函数的最大值，进而求出曲线 上的动点到曲线 距离的最值，从而求出曲线 上的动点到曲线 距离的取值范围。
23.【解析】【分析】〔1〕利用零点分段法结合条件，进而求出绝对值不等式的解集。
〔2〕利用绝对值的定义将函数f(x)转化为分段函数，再利用分段函数的图象判断分段函数的单调性，进而求出分段函数的最小值， 要使 对任意 恒成立，只需 ，即， 再利用同号为正、异号为负，进而求出实数m的取值范围。