

2021届广西钦州市、玉林市、柳州市高三理数第二次模拟考试试卷及答案
展开高三理数第二次模拟考试试卷
一、单项选择题
1.集合 , ,那么 〔 〕
A. B. C. D.
2.复数 〔i为虚数单位〕的虚部是〔 〕
A. B. C. D.
3.偶函数 在 上是减函数,假设 ,那么 的大小关系为〔 〕
A. B. C. D.
4.2021年,受新冠肺炎疫情的影响,在全国的许多地方都采取了在家线上学习的方式,此种方式对学生的自制力、自觉性有极高的要求.某校某学习小组调查研究“学生线上学习时智能 对学习成绩的影响〞,得到了如下样本数据:
不使用
使用
合计
优秀
8
4
12
不优秀
2
16
18
合计
10
20
30
附 , .
根据表中的数据,以下说法中正确的选项是〔 〕
A. 有99.5%的把握认为中学生使用 对学习无影响
B. 有99.5%的把握认为中学生使用 对学习有影响
C. 在犯错误的概率不超过0.001的前提下认为中学生使用 对学习无影响
D. 在犯错误的概率不超过0.001的前提下认为中学生使用 对学习有影响
5.函数 的大致图象可能是 ( )
A. B.
C. D.
6.某校迎新晚会上有6个节目,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在第三位,且节目丙、丁必须排在一起.那么该校迎新晚会节目演出顺序的编排方案共有〔 〕
A. 36种 B. 48种 C. 72种 D. 120种
7.等差数列 的前n项和为 ,当首项 和公差d变化时, 是一个定值,那么以下选项中为定值的是〔 〕
A. B. C. D.
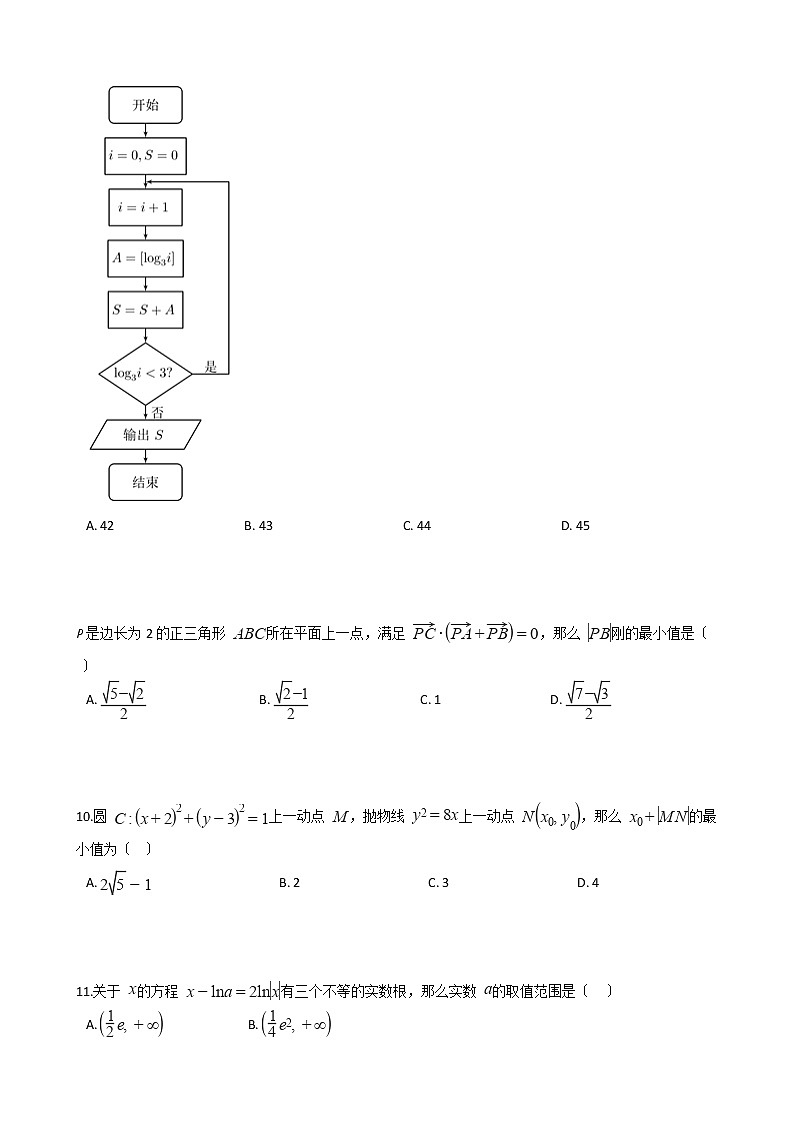
8.函数 称为高斯函数,其中不超过实数x的最大整数称为x的整数局部,记作 ,如图,那么输出的S值为〔 〕
A. 42 B. 43 C. 44 D. 45
P是边长为2的正三角形 所在平面上一点,满足 ,那么 刚的最小值是〔 〕
A. B. C. 1 D.
10.圆 上一动点 ,抛物线 上一动点 ,那么 的最小值为〔 〕
A. B. 2 C. 3 D. 4
11.关于 的方程 有三个不等的实数根,那么实数 的取值范围是〔 〕
A. B.
C. D.
12.正方体 的棱长为a , 点 分别为棱 的中点,以下结论中正确的个数是〔 〕
①过 三点作正方体的截面,所得截面为正六边形;② 平面 ;③异面直线 与 所成角的正切值为 ;④四面体 的体积等于等 .
A. 1 B. 2 C. 3 D. 4
二、填空题
13.正项等比数列 中, , ,记 为 的前 项和.假设 ,那么 ________.
14.如下列图,在边长为1的正方形 中任取一点 ,那么点 恰好取自阴影局部〔由对角线 及函数 围成〕的概率为________.
P为球O球面上一点,点M满足 ,过点M与 成 的平面截球O , 截面的面积为16π,那么球O的外表积为________.
16.在平面直角坐标系 中,直线 上存在点P , 过点P作圆 的切线,切点分别为 ,且 ,那么实数k的取值范围为________.
三、解答题
17.的内角 的对边分别为 ,函数 的一条对称轴为 ,且 .
〔1〕求A的值;
〔2〕假设 ,求 边上的高的最大值.
18.为了了解游客对景区的满意度,市旅游部门随机对景区的100名游客进行问卷调查〔总分值100分〕,这100名游客的评分分别落在区间 , 内,且游客之间的评分情况相互独立,得到统计结果如频率分布直方图所示.
〔1〕求这100名游客评分的平均值〔同一区间的数据用该区间数据的中点值为代表〕;
〔2〕视频率为概率,规定评分不低于80分为满意,低于80分为不满意,记游客不满意的概率为p.
①假设从游客中随机抽取m人,记这m人对景区都满意的概率为 ,求数列 的前4项和;
②为了提高游客的满意度,市旅游部门对景区设施进行了改进,游客人数明显增多,旅游部门随机抽取了3名游客进行了继续旅游的意愿调查,假设不再去旅游记 分,继续去旅游记1分,假设每位游客有继续旅游意愿的概率均为p , 记调查总得分为X , 求X的分布列与数学期望.
19.如图,三棱锥 中,底面 和侧面 都是等边三角形, .
〔1〕假设P点是线段 的中点,求证: 平面 ;
〔2〕点Q在线段 上且满足 ,求 与平面 所成角的正弦值.
20.椭圆 经过一点 ,左、右焦点分别为 ,P是椭圆上一动点,当 垂直于x轴时, .
〔1〕求椭圆C的标准方程;
〔2〕过点 ,斜率为k的直线l交椭圆于 两点,且 为钝角〔O为坐标原点〕,求k的取值范围.
21.函数 .
〔1〕当 时,求 的极值;
〔2〕假设对任意 ,都有 恒成立,求整数a的最大值.
22.在平面直角坐标系 中,直线 的参数方程为 〔 为参数〕.以坐标原点 为极点, 轴的非负半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
〔1〕求直线 的普通方程和曲线 的直角坐标方程;
〔2〕设 ,直线 与曲线 相交于 、 两点,假设 、 、 成等比数列,求实数 的值.
23.函数 .
〔1〕求不等式 的解集;
〔2〕假设关于x的不等式 恒成立,求实数a的取值范围.
答案解析局部
一、单项选择题
1.【解析】【解答】 , ,
因此, .
故答案为:B.
【分析】化简集合A,运用二次不等式的解法,化简集合B,再由交集的定义,即可得到所求.
2.【解析】【解答】因为 ,即复数 的虚部是 ,
故答案为:C.
【分析】 首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,整理成最简形式,得到复数的标准形式,得到虚部.
3.【解析】【解答】解:因为偶函数 在 上是减函数,
又 , ,
, , ,
那么 ,
所以 ,
那么 .
故答案为:C.
【分析】 根据函数奇偶性和单调性之间的关系,即可得到结论.
4.【解析】【解答】 ,
根据表中数据易知,有99.5%的把握认为中学生使用 对学习有影响,
故答案为:B.
【分析】 计算K的观测值K2 , 对照题目中的表格,得出统计结论.
5.【解析】【解答】由题意,函数 ,满足 ,
即 , ,得函数 是偶函数,其图象关于 轴对称,排除A、B项;
又由 ,排除D,
故可能的图象为C,
故答案为:C.
【分析】 判断函数的奇偶性和对称性,利用时的函数值的符号进行排除即可.
6.【解析】【解答】由题意丙、丁在一二位或四五位、五六位一,
因此方法数为 .
故答案为:A.
【分析】 先排丙丁,再考虑其他节目即可求解结论.
7.【解析】【解答】由等差数列的通项公式可得: 是一个定值,
所以 是一个定值,
所以 为一个定值,
故答案为:C.
【分析】 利用等差数列的通项公式、求和公式及其性质即可得出.
8.【解析】【解答】当 时, ;
时, ;
时, ;
时, ,
所以 .
故答案为:D.
【分析】 模拟执行程序的运行过程,得出输出的结果是累加计算S的值.
9.【解析】【解答】解:设边 的中点为 ,那么 ,
即为 ,那么点 在以 为直径的圆上,且 ,那么半径 ,
设 的中点为 ,那么 模的最小值为 .
故答案为:D.
【分析】 根据题意建立平面直角坐标系,设出点P的坐标,利用坐标表示向量,求出点P的轨迹是圆,从而求出的最小值.
10.【解析】【解答】如以下列图所示,过点 作抛物线 的准线 的垂线 ,垂足为点 ,
抛物线 的焦点为 ,圆 的圆心为 ,半径为1.
由抛物线的定义可得 ,那么 ,
.
当且仅当 、 、 、 四点共线且点 、 在线段 上时, 取得最小值为2.
故答案为:B.
【分析】 由圆的方程及抛物线的方程可得圆心C的坐标及半径和焦点F的坐标,由抛物线的性质可得,可得x0的表达式,由|MN|≥|CF|-|NF|-r=|CF|-|NF|-1,可得的最小值.
11.【解析】【解答】转为直线 与函数 有三个交点.
显然当 时,有一个交点:当 时,只需 与 有两个交点即可.
由 ,得 , 与 相切时,切点坐标为 ,
此时 .
由图象可知,当 时,关于 的方程 有三个不等的实数根.
故答案为:B.
【分析】 根据条件,把问题转化为直线 与函数 有3个不同的交点,结合导函数研究单调性和极值即可求解结论.
12.【解析】【解答】对于①,延长 分别与 的延长线交于 ,连接 交 于 ,设 与 的延长线交于 ,连接 交 于 ,交 于 ,连 ,
那么截面六边形 为正六边形,故①正确;
对于②, 与 相交,故 与平面 相交,所以②不正确;
对于③,连接 ,由条件有 ,所以 〔或其补角〕为异面直线 与 的夹角,在直角三角形 中, ,故③不正确;
对于④,四面体 的体积等于正方体的体积减去四个正三棱锥的体积,即为 ,故④正确;
所以正确的命题有2个
故答案为:B
【分析】 延长EF分别与B1A1 , B1B的延长线交于N,Q,连接GN交A1D1于H,设HG与B1C1的延长线交于P,连接PQ交CC1于I,交BC于M,连FH,HG,GI,IM,ME,得到截面六边形EFHGIM为正六边形;B1D1与HG相交,故B1D1与平面 EFG相交;取AD1的中点K,连接FK,EK,那么KE∥BD1 , 从而∠KEF就是异面直线EF与BD1的夹角,由此能求出异面直线EF与BD1的夹角的正切值;四面体ACB1D1的体积等于正方体的体积减去四个正三棱锥的体积.
二、填空题
13.【解析】【解答】设等比数列 的公比为 ,那么 ,且 ,且 ,
,解得 .
故答案为:7.
【分析】 根据题意,设正项等比数列{an}的公比为q,由a6=4a4 , 变形分析可得q的值,结合等比数列的前n项和公式计算可得答案.
14.【解析】【解答】由题意阴影局部面积为 ,
又正方形面积为 ,
所以所求概率为 .
故答案为: .
【分析】 根据题意,先求出正方形OABC的面积,再利用定积分求出阴影局部的面积,由几何概型公式计算可得答案.
15.【解析】【解答】如下列图:
设截面圆心为 ,
依题意得 ,
设 ,那么 ,
又 ,
所以 ,即球的半径为 ,
所以 ,
又截面的面积为 ,
所以 ,
解得 ,
在 中, ,
解得 ,所以球的半径为 ,
所以球的外表积是 ,
故答案为: 72π
【分析】 作出图形,设OO1=h,根据题意建立关于h的方程,进而求得球的半径,由此即可得解.
16.【解析】【解答】取 的中点 ,如下列图:
根据圆的切线性质: ,所以可得 ,所以 ,
由 ,
所以
由
所以 ,那么
点 到直线 的距离为
那么 或
所以
故答案为:
【分析】 采用数形结合,取 的中点 , 根据, 可计算 ,然后根据可得OP,最后利用点O到直线l的距离不大于OP,可得结果。
三、解答题
17.【解析】【分析】 〔1〕利用三角函数图象的对称轴经过函数图象的最高〔低〕点求φ,再求A;
〔2〕利用余弦定理和面积公式及根本不等式.
18.【解析】【分析】 〔1〕由频率分布直方图能求出这100名游客评分的平均值;
〔2〕①先求出游客不满意的概率, 从而 , 由此能求出数列{am}的前4项和;
②由题意X的可能取值为-3,-1,1,3,分别求出相应的概率,由此能求出X的分布列和E〔X〕.
19.【解析】【分析】 〔1〕利用等腰三角形可得垂直关系,再根据线面垂直的判定定理可得结论;
〔2〕取BC中点O,以O为坐标原点,OA为x轴,OB为y轴,OS为z轴,建立如下列图的空间直角坐标系,先求平面SAC的一个法向量 ,然后利用线面所成角正弦值即为 , 从而可求出所求.
20.【解析】【分析】 〔1〕由椭圆经过点 , 列方程组,解得a,b,c,进而可得答案;
〔2〕 当 时,设直线 : , 设 , , 联立椭圆的方程,结合韦达定理可得x1+x2 , x1x2 , 由∠AOB为钝角,得 且k≠0,进而可得答案.
21.【解析】【分析】 〔1〕求出函数的导数,令f'〔x〕=0,可得x的值,利用导函数的符号,判断函数的单调性,即可求得极值;
〔2〕 可化为 ,令 设 利用导数求出h〔x〕的最小值,从而可得整数a的最大值.
22.【解析】【分析】〔1〕 直接利用转换关系,把参数方程、极坐标方程和直角坐标方程之间进行转换;
〔2〕利用一元二次方程根和系数的关系式的应用求出结果.
23.【解析】【分析】 〔1〕去掉绝对值符号,转化不等式为不等式组,然后求解即可;
〔2〕不等式 恒成立等价于 ,利用绝对值的几何意义求解函数的最小值,然后求解指数不等式,推出a的范围即可.
广西柳州市2023届高三理数二模试卷附参考答案: 这是一份广西柳州市2023届高三理数二模试卷附参考答案,共11页。
2023届广西柳州市高三第三次模拟考试理数试题: 这是一份2023届广西柳州市高三第三次模拟考试理数试题,文件包含柳州市2023届高三第三次模拟考试理科数学参考答案pdf、柳州市2023届高三第三次模拟考试理科数学pdf等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。
广西钦州市2021届高三第二次模拟考试+数学(理)+Word版含答案练习题: 这是一份广西钦州市2021届高三第二次模拟考试+数学(理)+Word版含答案练习题,共12页。












