
2020-2021学年安徽省高二(上)开学数学试卷(文科)人教A版
展开1. 设集合A={x|x2−4≤0},B={x|2x+a≤0},且A∩B={x|−2≤x≤1},则a=( )
A.−4B.−2C.2D.4
2. 已知函数f(x)=,则f[f(4)]=( )
A.−1B.1C.2D.4
3. 在平行四边形ABCD中,E为BC的中点,F为AE的中点,则=( )
A.B.C.D.
4. 已知圆锥的底面积和侧面积之比为1:2,则圆锥的轴与母线所成的角为( )
A.B.C.D.
5. 已知θ是第二象限角,且,则=( )
A.B.C.D.
6. 函数f(x)=|x|−csx的零点个数为( )
A.0B.1C.2D.3
7. 若函数在x=a处取最小值,则a=( )
A.B.2C.4D.6
8. 已知a=lg20.3,b=lg0.32,c=20.3,则( )
A.b
9. 若x,y满足约束条件,则z=x−y的最小值为( )
A.−9B.−6C.−3D.−2
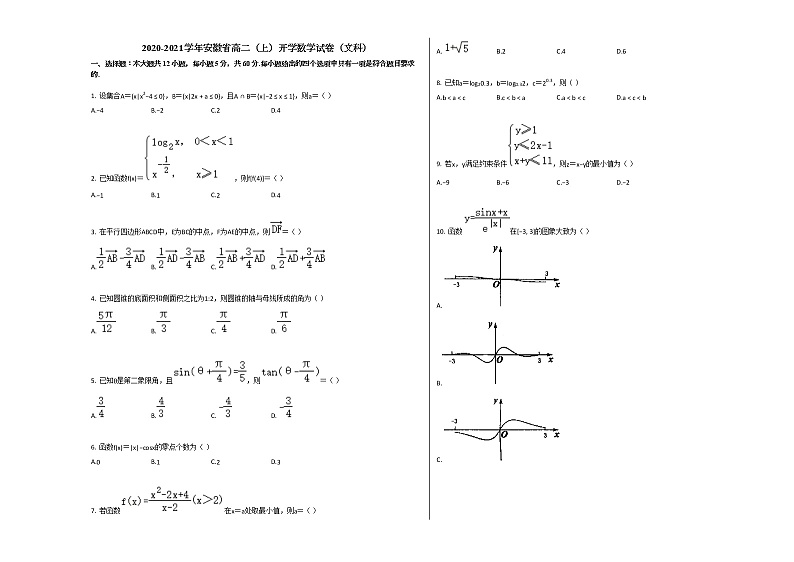
10. 函数在[−3, 3]的图象大致为( )
A.
B.
C.
D.
11. 已知函数f(x)=cs2x−2sin2x,则( )
A.f(x)的最小正周期为2π,最大值为3
B.f(x)的最小正周期为2π,最大值为1
C.f(x)的最小正周期为π,最大值为3
D.f(x)的最小正周期为π,最大值为1
12. 如图,在长方体ABCD−A1B1C1D1中,,AD=4,异面直线BD与AC1所成角的余弦值为,则该长方体外接球的表面积为( )
A.50πB.100πC.400πD.
二、填空题:本大题共4小题,每小题5分,共20分.
函数y=的定义域为________.
在△ABC中,b=7,,,则a=________.
已知向量,满足,且,,则与的夹角为________.
已知定义在R上的函数f(x)满足f(−x)=−f(x),且在[0, +∞)上是增函数,当时,f(asinθ)+f(sinθ−a)>0恒成立,则a的取值范围是________.
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
已知数列{an}满足an+2+an=2an+1,n∈N∗,其前n项和为Sn,且a4=S3=−3.
(1)求数列{an}的通项公式;
(2)求数列的前n项和.
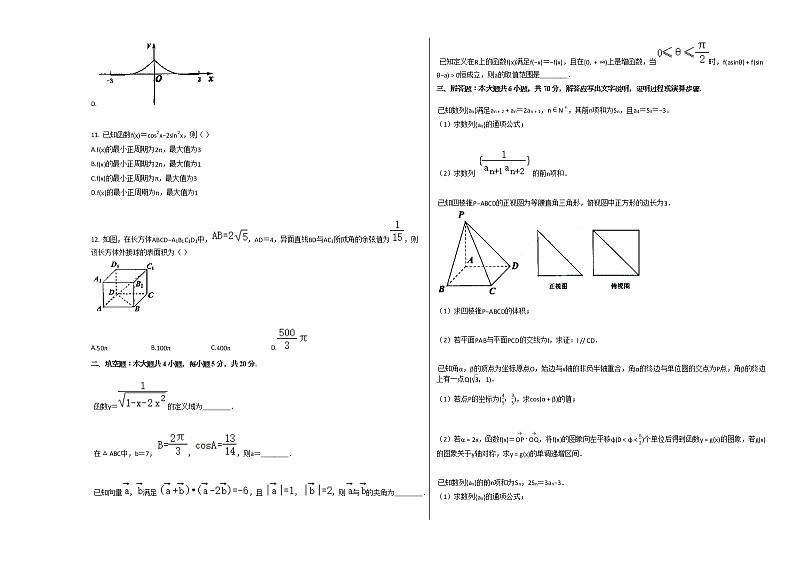
已知四棱锥P−ABCD的正视图为等腰直角三角形,俯视图中正方形的边长为3.
(1)求四棱锥P−ABCD的体积;
(2)若平面PAB与平面PCD的交线为l,求证:l // CD.
已知角α,β的顶点为坐标原点O,始边与x轴的非负半轴重合,角α的终边与单位圆的交点为P点,角β的终边上有一点Q(3,1).
(1)若点P的坐标为(45,35),求cs(α+β)的值;
(2)若α=2x,函数f(x)=OP→⋅OQ→,将f(x)的图象向左平移φ(0<φ<π2)个单位后得到函数y=g(x)的图象,若g(x)的图象关于y轴对称,求y=g(x)的单调递增区间.
已知数列{an}的前n项和为Sn,2Sn=3an−3.
(1)求数列{an}的通项公式;
(2)记,设数列{bn}的前n项和为Tn,求证:.
△ABC的内角A,B,C的对边分别为a,b,c.已知acsB=(2c−b)csA.
(1)求A;
(2)若△ABC为锐角三角形,且a=1,求△ABC周长的取值范围.
已知函数.
(1)若f(x)是偶函数,求a的值;
(2)当a<−4时,若关于x的方程f(−2x2+4x+3+a)=2在[−1, 2]上恰有两个不同的实数解,求a的取值范围.
参考答案与试题解析
2020-2021学年安徽省高二(上)开学数学试卷(文科)
一、选择题:本大题共12小题,每小题5分,共60分.每小题给出的四个选项中只有一项是符合题目要求的.
1.
【答案】
B
【考点】
交集及其运算
【解析】
由二次不等式和一次不等式的解法,化简集合A,B,再由交集的定义,可得a的方程,解方程可得a.
【解答】
集合A={x|x2−4≤0}={x|−2≤x≤2},B={x|2x+a≤0}={x|x≤−12a},
由A∩B={x|−2≤x≤1},可得−12a=1,
则a=−2.
2.
【答案】
A
【考点】
对数的运算性质
求函数的值
函数的求值
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
A
【考点】
向量的线性运算性质及几何意义
向量数乘的运算及其几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
D
【考点】
旋转体(圆柱、圆锥、圆台)
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
B
【考点】
两角和与差的三角函数
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
C
【考点】
函数的零点与方程根的关系
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
C
【考点】
基本不等式及其应用
函数的最值及其几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
C
【考点】
对数值大小的比较
【解析】
此题暂无解析
【解答】
此题暂无解答
9.
【答案】
C
【考点】
简单线性规划
【解析】
此题暂无解析
【解答】
此题暂无解答
10.
【答案】
C
【考点】
函数的图象与图象的变换
【解析】
此题暂无解析
【解答】
此题暂无解答
11.
【答案】
D
【考点】
三角函数的周期性
二倍角的三角函数
三角函数的最值
【解析】
此题暂无解析
【解答】
此题暂无解答
12.
【答案】
B
【考点】
球的表面积和体积
异面直线及其所成的角
球内接多面体
【解析】
此题暂无解析
【解答】
此题暂无解答
二、填空题:本大题共4小题,每小题5分,共20分.
【答案】
【考点】
函数的定义域及其求法
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
3
【考点】
正弦定理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
【考点】
平面向量数量积的性质及其运算
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
(−∞, 0)
【考点】
奇偶性与单调性的综合
函数恒成立问题
【解析】
此题暂无解析
【解答】
此题暂无解答
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
【答案】
∵ an+2+an=2an+5,∴ {an}为等差数列.
∵ a4=S3=−6,∴ ,∴ a1=2,d=−1
∴ an=a1+(n−5)d=1−n.……………………………………………
令,则
∴ 的前n项和为
【考点】
数列的求和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
由俯视图与正视图可知,该四棱锥的底面是边长为3的正方形.
∴ ;
证明:
∵ CD // AB,CD⊄平面PAB,
∴ CD // 平面PAB,
又平面PAB∩平面PCD=l,CD⊂平面PCD,
∴ l // CD.
【考点】
直线与平面平行
棱柱、棱锥、棱台的体积
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
由三角函数的定义可得csα=45,sinα=35,csβ=32,sinβ=12.
∴ cs(α+β)=csαcsβ−sinαsinβ=45×32−35×12=43−310.
由题意P(cs2x, sin2x),Q(3,1),∵ 函数f(x)=OP→⋅OQ→,
∴ f(x)=3cs2x+sin2x=2cs(2x−π6).
∵ 将f(x)的图象向左平移φ(0<φ<π2)个单位后得到函数y=g(x)的图象,
∴ g(x)=2cs[2(x+φ)−π6]=2cs(2x+2φ−π6).
∵ g(x)的图象关于y轴对称,∴ 2φ−π6=kπ,∴ φ=kπ2+π12(k∈Z),
∵ 0<φ<π2,∴ φ=π12.
∴ g(x)=2cs2x,令2k−π≤2x≤2kπ,得kπ−π2≤x≤kπ,
∴ g(x)的单调递增区间为[kπ−π2,kπ](k∈Z).
【考点】
任意角的三角函数
函数y=Asin(ωx+φ)的图象变换
【解析】
(1)由题意利用任意角的三角函数的定义,求得α、β的正弦值和余弦值,再利用两角和的余弦公式求得结果.
(2)由题意利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用余弦函数的单调性,求得g(x)的单调递增区间.
【解答】
由三角函数的定义可得csα=45,sinα=35,csβ=32,sinβ=12.
∴ cs(α+β)=csαcsβ−sinαsinβ=45×32−35×12=43−310.
由题意P(cs2x, sin2x),Q(3,1),∵ 函数f(x)=OP→⋅OQ→,
∴ f(x)=3cs2x+sin2x=2cs(2x−π6).
∵ 将f(x)的图象向左平移φ(0<φ<π2)个单位后得到函数y=g(x)的图象,
∴ g(x)=2cs[2(x+φ)−π6]=2cs(2x+2φ−π6).
∵ g(x)的图象关于y轴对称,∴ 2φ−π6=kπ,∴ φ=kπ2+π12(k∈Z),
∵ 0<φ<π2,∴ φ=π12.
∴ g(x)=2cs2x,令2k−π≤2x≤2kπ,得kπ−π2≤x≤kπ,
∴ g(x)的单调递增区间为[kπ−π2,kπ](k∈Z).
【答案】
∵ 2Sn=3an−4
∴ 2Sn−1=2an−1−3(n≥6)
两式相减,得2an=3an−8an−1,∴ an=3an−3(n≥2)
又a1=5,∴ {an}为等比数列,公比为q=3
∴ .………………………………………
证明:,
∴ ,
,
两式相减,得
化简得.……………………………………………
∵ n∈N∗,∴ Tn<1,
∴ ,∴ ,
∴ Tn关于n单调递增,∴ ,∴ .………………………
【考点】
数列递推式
数列的求和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
解法一:由已知,得acsB+bcsA=2ccsA;
由正弦定理,得sinAcsB+sinBcsA=2sinCcsA,
即sin(A+B)=4sinCcsA;
又sin(A+B)=sinC,
所以sinC=2sinCcsA.
又sinC≠0,所以;
又0
化简得b2+c2−a2=bc,
所以;
又0
所以,;
所以=.
因为△ABC为锐角三角形,
所以得,
解得.
所以;
即△ABC周长的取值范围是.
【考点】
余弦定理
正弦定理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
若函数偶函数,
即,变形可得4ax+1=4(1−a)x+4x,
则有a=5;
,
∵ a<−4,∴ y=5(2a−1)x,y=4−x都在R上单调递减,∴ 函数y=f(x)在R上单调递减,
又f(0)=2,∴ f(−2x7+4x+3+a)=f(0),
∴ −4x2+4x+8+a=0,
∴ a=2x3−4x−3,x∈[−8,
由图象知,当−5
又∵ a<−3,∴ −5
【考点】
函数奇偶性的性质与判断
函数的零点与方程根的关系
【解析】
此题暂无解析
【解答】
此题暂无解答
2020-2021学年安徽省高二(上)开学数学试卷人教A版: 这是一份2020-2021学年安徽省高二(上)开学数学试卷人教A版,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年安徽省高二(上)期中数学试卷(文科)人教A版: 这是一份2020-2021学年安徽省高二(上)期中数学试卷(文科)人教A版,共10页。试卷主要包含了解答题等内容,欢迎下载使用。
2020-2021学年安徽省高二(上)开学数学试卷(理科)人教A版: 这是一份2020-2021学年安徽省高二(上)开学数学试卷(理科)人教A版,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












