

2020-2021学年河南省漯河市高一(下)4月月考数学(文)试卷人教A版
展开
这是一份2020-2021学年河南省漯河市高一(下)4月月考数学(文)试卷人教A版,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1. 某公司有52名员工,要从中抽取10名员工参加国庆联欢活动,若采用系统抽样,则该公司每个员工被抽到的机会为( )
A.15B.14C.526D.213
2. 高三某班有34位同学,座位号记为01,02,⋯,34,用下面的随机数表选取5组数作为参加青年志愿者活动的五位同学的座号.选取方法是从随机数表第一行的第6列和第7列数字开始,由左到右依次选取两个数字,则选出来的第4个志愿者的座号为( )
A.23B.09C.02D.16
3. 某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工为7人,则样本容量为( )
A.7B.15C.25D.35
4. 演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数B.平均数C.方差D.极差
5. 设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
A.15B.25C.12D.45
6. 某学校为了解1000名新生的身体素质,将这些学生编号为1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是( )
A.8号B.200号C.616号D.815号
7. 如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
A.3,5B.5,5C.3,7D.5,7
8. 执行如图所示的程序框图,输出的S值为( )
A.2B.4C.8D.16
9. 函数y=−12x+2的相关系数为( )
A.−12B.−1C.1D.2
10. 如图是一个射击靶的示意图,其中每个圆环的宽度与中心圆的半径相等.某人朝靶上任意射击一次没有脱靶,则其命中深色部分的概率为( )
A.25B.12C.37D.38
11. 如图是求12+12+12的程序框图,图中空白框中应填入( )
A.A=12+AB.A=2+1AC.A=11+2AD.A=1+12A
12. 甲、乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少有一艘在停靠泊位时必须等待的概率为( )
A.19B.89C.512D.716
二、填空题
某制造商今年3月份生产了一批乒乓球,随机抽取100个进行检查,测得每个乒乓球的直径(单位:mm),将数据分组如下:
若用上述频率近似概率,已知标准乒乓球的直径为40.00mm,则这批兵乓球的直径误差不超过0.03mm的概率是________.
围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为17,从中取出2粒都是白子的概率是1235,则从中任意取出2粒恰好颜色不同的概率是________.
若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率是________.
一个三位自然数百位,十位,个位上的数字依次为a,b,c,当且仅当有两个数字的和等于第三个数字时称为“有缘数”(如213,134等),若a,b,c∈{1, 2, 3, 4},且a,b,c互不相同,则这个三位数为”有缘数”的概率是________.
三、解答题
利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率;
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
疫情期间口罩需求量大增,某医疗器械公司开始生产KN95口罩,并且对所生产口罩的质量按指标测试分数进行划分,其中分数不小于70的为合格品,否则为不合格品,现随机抽取100件口罩进行检测,其结果如下:
(1)根据表中数据,估计该公司生产口罩的不合格率;
(2)根据表中数据,估计该公司口罩的平均测试分数;
(3)若用分层抽样的方式按是否合格从所生产口罩中抽取5件,再从这5件口罩中随机抽取2件,求这2件口罩全是合格品的概率.
2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如表,其中“O”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:∘C)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20, 25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
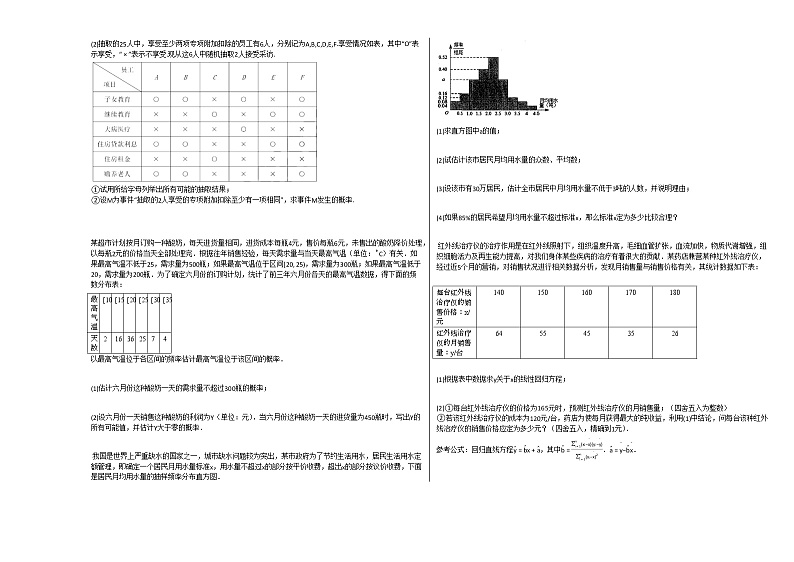
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,居民生活用水定额管理,即确定一个居民月用水量标准x,用水量不超过x的部分按平价收费,超出x的部分按议价收费,下面是居民月均用水量的抽样频率分布直方图.
(1)求直方图中a的值;
(2)试估计该市居民月均用水量的众数、平均数;
(3)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(4)如果85%的居民希望月均用水量不超过标准x,那么标准x定为多少比较合理?
红外线治疗仪的治疗作用是在红外线照射下,组织温度升高,毛细血管扩张,血流加快,物质代谢增强,组织细胞活力及再生能力提高,对我们身体某些疾病的治疗有着很大的贡献.某药店兼营某种红外线治疗仪,经过近5个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有关,其统计数据如下表:
(1)根据表中数据求y关于x的线性回归方程;
(2)①每台红外线治疗仪的价格为165元时,预测红外线治疗仪的月销售量;(四舍五入为整数)
②若该红外线治疗仪的成本为120元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到1元).
参考公式:回归直线方程y=bx+a,其中b=i=1n(xi−x¯)(yi−y¯)i=1n(xi−x¯)2.a=y¯−bx¯.
参考答案与试题解析
2020-2021学年河南省漯河市高一(下)4月月考数学(文)试卷
一、选择题
1.
【答案】
C
【考点】
系统抽样方法
【解析】
系统抽样中,每个个体抽到的概率相同.
【解答】
解:因为系统抽样中,每个个体被抽到的概率相同,即1052=526.
故选C.
2.
【答案】
D
【考点】
简单随机抽样
【解析】
试题分析:从随机数表第一行的第6列和第7列数字35开始,由左到右依次选取两个数字,不超过34的依次为:,16.17,第四个志愿者的座号为16,故选D.
【解答】
解:根据题意利用随机数表法,依次抽取的样本数据为:
21,32,09,16,17,
所以第4个数据是16.
故选D.
3.
【答案】
B
【考点】
分层抽样方法
【解析】
先计算青年职工所占的比例,再根据青年职工抽取的人数计算样本容量即可.
【解答】
解:由题得青年职工、中年职工、老年职工三层之比为7:5:3,所以样本容量为7715=15.
故选B.
4.
【答案】
A
【考点】
众数、中位数、平均数
极差、方差与标准差
【解析】
此题暂无解析
【解答】
解:对于一组数据,去掉最低分与最高分后,中位数一定不会改变,故A选项正确;
对于一组数据,去掉最低分与最高分后,平均数可能会变,也可能不变,故B选项错误;
对于一组数据,去掉最低分与最高分后,方差可能变也可能不变,故C选项错误;
对于一组数据,去掉最低分与最高分后,极差可能变也可能不变,故D选项错误.
故选A.
5.
【答案】
A
【考点】
列举法计算基本事件数及事件发生的概率
【解析】
先求出基本事件总数,再求出三点共线的基本事件个数,然后利用概率公式求得三点共线的概率.
【解答】
解:如图,
,
从O,A,B,C,D5个点中任取3个有
O,A,B,{O,A,C},{O,A,D},{O,B,C},{O,B,D},
{O,C,D},{A,B,C},{A,B, D},A,C,D,B,C,D,
共10种不同取法,3点共线只有A,O,C与B,O,D共2种情况,
由古典概型的概率计算公式知,取到3点共线的概率为210=15.
故选A.
6.
【答案】
C
【考点】
系统抽样方法
【解析】
此题暂无解析
【解答】
解:由已知将1000名学生分成100组,每组10名学生,用系统抽样46号学生被抽到,所以第一组抽到6号,
第二组抽到16号,
第三组抽到26号,
⋯,
第n组抽到6+10(n−1)=10n−4号,n∈N∗,1≤n≤100,
若8=10n−4,则n=65,不合题意;若200=10n−4,则n=20.4,不合题意;
若616=10n−4,则n=62,符合题意;若815=10n−4,则n=81.9不合题意.
故选C.
7.
【答案】
A
【考点】
茎叶图
众数、中位数、平均数
【解析】
由已知有中这两组数据的中位数相等,且平均值也相等,可得x,y的值.
【解答】
解:由已知中甲组数据的中位数为65,
故乙组数据的中位数也为65,
即y=5,
因为两组平均数相等,
所以59+61+67+65+785=56+65+62+74+(70+x)5,
故x=3.
故选A.
8.
【答案】
C
【考点】
条件结构的应用
【解析】
按照流程图判断即可.
【解答】
解:第1次循环后 S=1, k=1;
第2次循环后 S=2, k=2;
第3次循环后 S=8 ,k=3;
第4次循环后3
相关试卷
这是一份2020-2021学年河南省漯河市高二(下)3月月考数学(文)试卷人教A版,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2020-2021学年河南省漯河市高二(下)3月月考数学(理)试卷人教A版,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2020-2021学年河南省漯河市高一(下)6月月考数学(理)试卷人教A版,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









