高中数学人教A版 (2019)必修 第一册5.6 函数 y=Asin（ ωx ＋ φ）巩固练习

课时同步练习(五十)　函数y＝Asin(x＋φ)

(建议用时：60分钟)

[合格基础练]

一、选择题

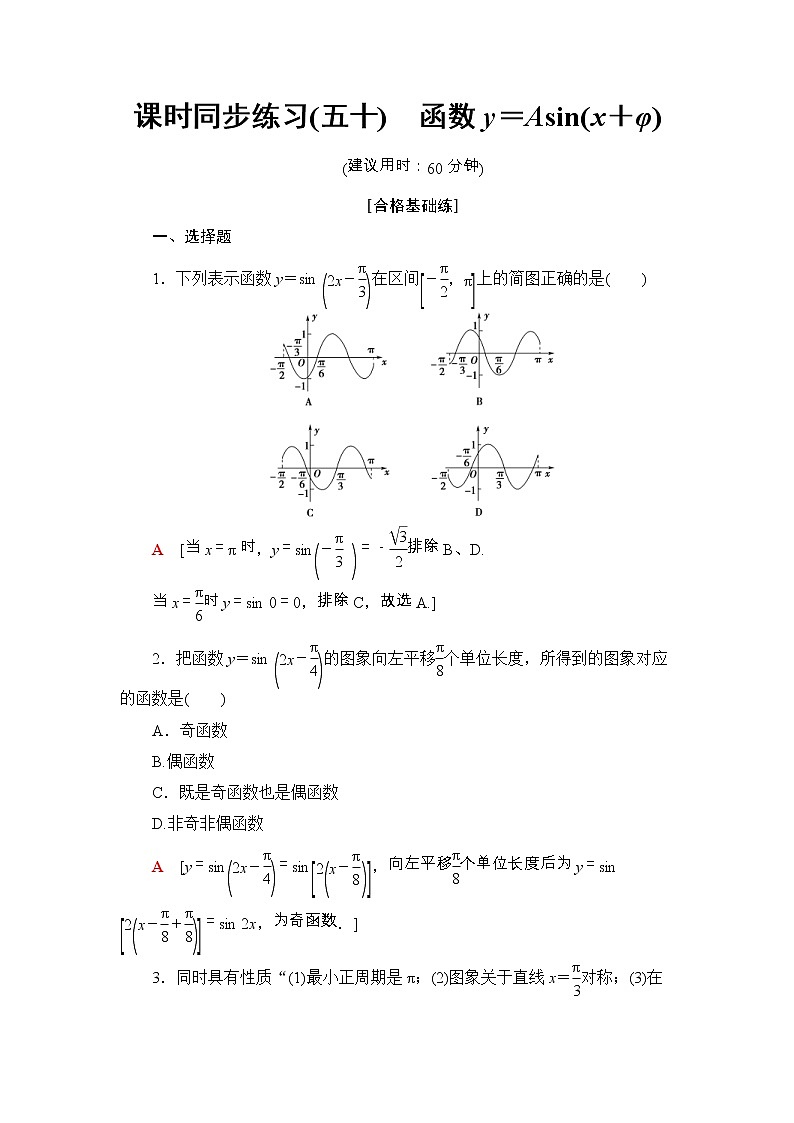
1．下列表示函数y＝sin在区间上的简图正确的是(　　)

A　[当x＝π时，y＝sin＝－排除B、D.

当x＝时y＝sin 0＝0，排除C，故选A.]

2．把函数y＝sin的图象向左平移个单位长度，所得到的图象对应的函数是(　　)

A．奇函数

B.偶函数

C．既是奇函数也是偶函数

D.非奇非偶函数

A　[y＝sin＝sin，向左平移个单位长度后为y＝sin＝sin 2x，为奇函数．]

3．同时具有性质“(1)最小正周期是π；(2)图象关于直线x＝对称；(3)在上单调递增”的一个函数是(　　)

A．y＝sin B．y＝cos

C．y＝sin   D．y＝cos

C　[由(1)知T＝π＝，ω＝2，排除A.由(2)(3)知x＝时，f(x)取最大值，验证知只有C符合要求．]

4．已知函数f(x)＝Asin(ωx＋φ)＋B的一部分图象如图所示，若A＞0，ω＞0，|φ|＜，则(　　)

A．B＝4   B．φ＝

C．ω＝1   D．A＝4

B　[由函数图象可知f(x)min＝0，f(x)max＝4.

所以A＝＝2，B＝＝2.

由周期T＝＝4知ω＝2.

由f＝4得2sin＋2＝4，

sin＝1，又|φ|＜，故φ＝.]

5．已知函数f(x)＝cos(ω＞0)的相邻两个零点的距离为，要得到y＝f(x)的图象，只需把y＝cos ωx的图象(　　)

A．向右平移个单位 B．向左平移个单位

C．向右平移个单位   D．向左平移个单位

A　[由已知得＝2×，故ω＝2.

y＝cos 2x向右平移个单位可得y＝cos 2＝cos的图象．]

二、填空题

6．要得到函数y＝sinx的图象，只需将函数y＝sin的图象向右平移________个单位．

　[由于y＝sin＝sin，故要得到y＝sinx的图象，只要将y＝sin的图象向右平移个单位．]

7．将函数y＝sin的图象向右平移个单位长度，再将图象上各点的横坐标扩大到原来的3倍(纵坐标不变)，则所得的函数解析式是________．

y＝sin　[y＝sin3x＋

y＝sin＝sin

y＝sin，

故所得的函数解析式是y＝sin.]

8．某同学利用描点法画函数y＝Asin (ωx＋φ)(其中0<A≤2,0<ω<2，－<φ<)的图象，列出的部分数据如下表：

经检查，发现表格中恰有一组数据计算错误，请你根据上述信息推断函数y＝Asin (ωx＋φ)的解析式应是________．

y＝2sin　[在平面直角坐标系中描出这五个点，如图所示．

根据函数图象的大致走势，

可知点(1,0)不符合题意；

又因为0<A≤2，函数图象过(4，－2)，

所以A＝2.

因为函数图象过(0,1)，∴2sin φ＝1，

又∵－<φ<，∴φ＝，

由(0,1)，(2,1)关于直线x＝1对称，

知x＝1时函数取得最大值2，

因此函数的最小正周期为6.

∴ω＝.]

三、解答题

9．已知函数f(x)＝Asin(ωx＋φ)(A＞0，ω＞0，|φ|＜)的部分图象如图所示．

(1)求函数f(x)的解析式；

(2)如何由函数y＝sin x的图象通过相应的平移与伸缩变换得到函数f(x)的图象，写出变换过程．

[解]　(1)由图象知A＝1.f(x)的最小正周期T＝4×＝π，故ω＝＝2，

将点代入f(x)的解析式得sin＝1，

又|φ|＜，∴φ＝.故函数f(x)的解析式为f(x)＝sin.

(2)变换过程如下：

y＝sin x图象上的y＝sin 2x的图象，再把y＝sin 2x的图象,向左平移个单位y＝sin的图象．

10．已知函数f(x)＝2cos2ωx－1＋2sin ωxcos ωx(0＜ω＜1)，直线x＝是函数f(x)的图象的一条对称轴．

(1)求函数f(x)的单调递增区间；

(2)已知函数y＝g(x)的图象是由y＝f(x)的图象上各点的横坐标伸长到原来的2倍，然后再向左平移个单位长度得到的，若g＝，α∈，求sin α的值．

[解]　(1)f(x)＝cos 2ωx＋sin 2ωx＝2sin2ωx＋，

由于直线x＝是函数f(x)＝2sin的图象的一条对称轴，

所以ω＋＝kπ＋(k∈Z)，

解得ω＝k＋(k∈Z)，

又0＜ω＜1，所以ω＝，

所以f(x)＝2sin.

由2kπ－≤x＋≤2kπ＋(k∈Z)，

得2kπ－≤x≤2kπ＋(k∈Z)，

所以函数f(x)的单调递增区间为2kπ－，2kπ＋(k∈Z)．

(2)由题意可得g(x)＝2sin，

即g(x)＝2cos，

由g＝2cos＝2cos＝，得cos＝，

又α∈，故＜α＋＜，

所以sin＝，

所以sin α＝sin

＝sin·cos－cos·sin

＝×－×＝.

[等级过关练]

1．已知a是实数，则函数f(x)＝1＋asin ax的部分图象不可能是(　　)

D　[当a＝0时，f(x)＝1，是选项C，当a≠0时，

函数f(x)＝1＋asin ax的周期T＝，

振幅为|a|，所以当|a|＜1时，T＞2π.

当|a|＞1时T＜2π，由此可知A，B有可能出现，D不可能．]

2．函数y＝sin 2x的图象向右平移φ个单位长度(φ＞0)得到的图象恰好关于x＝对称，则φ的最小值是________．

　[函数y＝sin 2x的图象向右平移后得到y＝sin[2(x－φ)]的图象，而x＝是对称轴，即2＝kπ＋(k∈Z)，所以φ＝－(k∈Z)．又φ＞0当k＝－1时，φ取得最小值.]

3．函数f(x)＝3sin的图象为C，则以下结论中正确的是________．(写出所有正确结论的编号)

①图象C关于直线x＝对称；

②图象C关于点对称；

③函数f(x)在区间内是增函数；

④由y＝3sin 2x的图象向右平移个单位长度可以得到图象C.

②③　[f＝3sin

＝3sin＝－.

f＝3sin＝0，

故①错，②正确．

令－＋2kπ≤2x－≤＋2kπ，k∈Z，

解得－＋kπ≤x≤π＋kπ，k∈Z，故③正确．

函数y＝3sin 2x的图象向右平移个单位长度，得到函数y＝3sin 2＝3sin的图象，故④错．]

4．函数y＝2sin πx－(－2≤x≤4)的所有零点之和为________．

8　[函数y＝2sin πx－(－2≤x≤4)的零点即

方程2sin πx＝的根，

作函数y＝2sin πx与y＝的图象如下：由图可知共有8个公共点所以原函数有8个零点．

y＝2sin πx－＝2sin π(1－x)－，

令t＝1－x，则y＝2sin πt－，t∈[－3,3]，

该函数是奇函数，故零点之和为0.所以原函数的零点之和为8.]

5．已知函数f(x)＝Asin(ωx＋φ)＋B(A＞0，ω＞0，|φ|＜)的一系列对应值如下表：

(1)根据表格提供的数据求函数f(x)的一个解析式；

(2)根据(1)的结果，若函数y＝f(kx)(k＞0)的最小正周期为，当x∈时，方程f(kx)＝m恰有两个不同的实数解，求实数m的取值范围．

[解]　(1)设f(x)的最小正周期为T，则T＝－＝2π，由T＝，得ω＝1，又解得令ω·＋φ＝，即＋φ＝，解得φ＝－，∴f(x)＝2sin＋1.(答案不唯一)

(2)∵函数y＝f(kx)＝2sin＋1的最小正周期为，且k＞0，∴k＝3.令t＝3x－，∵x∈，

∴t∈，如图所示，

当sin t＝s在上有两个不同的实数解时，s∈，∴当x∈时，由方程f(kx)＝m恰有两个不同的实数解得m∈[＋1,3)，即实数m的取值范围是[＋1,3)．