2021届高中数学一轮复习 高考命题新思维之四 课件 （文数）（北师大版）

这是一份2021届高中数学一轮复习 高考命题新思维之四 课件 （文数）（北师大版），共16页。

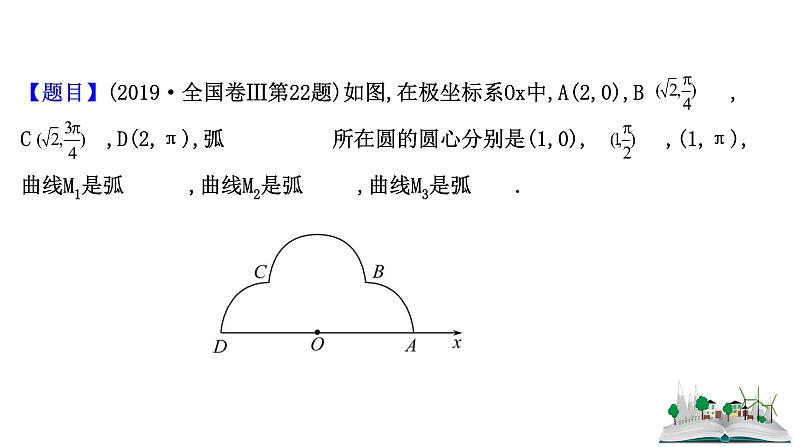
【题目】(2019·全国卷Ⅲ第22题)如图,在极坐标系Ox中,A(2,0),B 　 ,C 　　 ,D(2,π),弧 　　 所在圆的圆心分别是(1,0), 　　 ,(1,π),曲线M1是弧 　　 ,曲线M2是弧 　 ,曲线M3是弧 .
(1)分别写出M1,M2,M3的极坐标方程.(2)曲线M由M1,M2,M3构成,若点P在M上,且|OP|= ,求点P的极坐标.
【试题点评】本题命制新颖,别出心裁,以一个“云”形状的图形,要求考生求极坐标方程.这种极坐标形式的问题在高考中不多见.命题人的“煞费苦心”让考生感觉这朵云“好凄美”.这些题目看似变难了,其实是出题方式变得灵活了,更加符合新高考的要求,突出考查数学建模、直观想象、数学运算的核心素养.
【命题探源】在2016年上海高考数学试卷中,也出现过类似给出图形求曲线的极坐标方程的题目,其来源为数学家笛卡尔的心形线.人教版教材中,也出现过自己选择适当的极坐标系求圆的极坐标方程、直线的极坐标方程等.
【高考声音】这道题传递了一个高考信息,回归课本,基础要绝对扎实.虽然题目比较新颖,但是只要紧扣教材,就能很好地解答.这些试题不仅对所学的知识进行考查,而且还与实际生活联系得更加紧密了.高考试题不但考查考生的做题的速度和准确度,还拓宽了知识的广度和宽度,更加考验学生对知识灵活运用的能力.
【解法探究】(1)将三个过原点的圆方程列出,注意题中要求的是弧,所以要注意方程中θ的取值范围.(2)根据条件ρ= 逐个方程代入求解,最后解出P点的极坐标.
【解析】(1)如图所示,极坐标A(2,0),B 　　 ,C 　　 ,D(2,π)转化为直角坐标为A(2,0),B(1,1),C(-1,1),D(-2,0).则M1,M2,M3的圆心坐标分别为(1,0),(0,1),(-1,0).
M1,M2,M3所在圆的方程为(x-1)2+y2=1,x2+(y-1)2=1,(x+1)2+y2=1,设x=ρ cs θ,y=ρ sin θ,则M1,M2,M3所在圆的极坐标方程分别为M1:ρ=2cs θ 　　　 ,M2:ρ=2cs 　　=2sin θ 　　　　　 ,M3:ρ=2cs(θ-π)=-2cs θ 　　　　 .
(2)设P(ρ,θ),由题设及(1)知若2cs θ= 　　　　　 ,解得θ= ,若2sin θ= 　　　　　,解得θ= 或θ= .若-2cs θ= 　　　　　　 ,解得θ= .故P的极坐标为
【拓展赏析】1.其实这道题并不难:考生之所以认为这道题难,其主要原因是长期的应试训练,造成了学生思维的僵化的结果.由于没有心理准备,当面对新的变化时容易引起情绪上的波动,从而觉得试题变难了.其实只要静下心来好好读读题目,也不难发现那是几个曲线的组合.教材上的标准模型不见了,取而代之的是几个标准模型的组合.
2.把高考拉进了现实:现实社会中哪有标准的模型,几乎每件事都是复杂的不能再复杂的事情的组合.要想解决现实的问题,只有努力地透过现象看本质,找出其中所包含的模型,才有可能解决现实中的问题.“死记硬背”“机械刷题”“题海战术”,已不适合新高考.高考试卷中出现了一朵云,这朵云把高考拉进了现实.值得师生在备考中细加品味.
【新题试做】(2019·北京高考)数学中有许多形状优美、寓意美好的曲线,曲线C:x2+y2=1+|x|y就是其中之一(如图).给出下列三个结论:
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);②曲线C上任意一点到原点的距离都不超过 ;③曲线C所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是(　　)A.①　　　　　B.②　　　　　C.①②　　　　　D.①②③
【解析】选C.对①,令x=0得y=±1,即曲线C过整点(0,±1);令x=1得1+y2=1+y,y=0,1,即曲线C过整点(1,0),(1,1),又由曲线关于y轴对称知,曲线C过整点(-1,0),(-1,1),结合图形知,曲线C不过其他整点,所以①正确;对②,只需考虑第一象限内的点,即x>0,y>0,设C上的点(x,y)到原点的距离为d,