

2020-2021学年江西省赣州市高一(上)期末考试数学试卷北师大版
展开1. 若函数fx=x3, x≥0,x+2,x<0, 则ff−1=( )
A.−1B.1C.−27D.27
2. 若集合A=x∈N|x≤2, B=x|y=lg2x,则A∩B=( )
A.1,2B.{0,1,2}C.x|0
3. 设a=lg213,b=20.3,c=tanπ12的大小关系是( )
A.a
4. 已知映射f:A→B.若集合A中元素x在对应法则f下的像是|x|,则B中元素2的原像可以是( )
A.−2B.2C.±2D.2
5. 若圆的半径为6cm,则圆心角为π18的扇形面积是( )
A.π2cm2B.πcm2C.3π2cm2D.2πcm2
6. 若函数fx=2x+x−4的零点所在区间为k,k+1k∈Z,则k的值是( )
A.1B.2C.3D.4
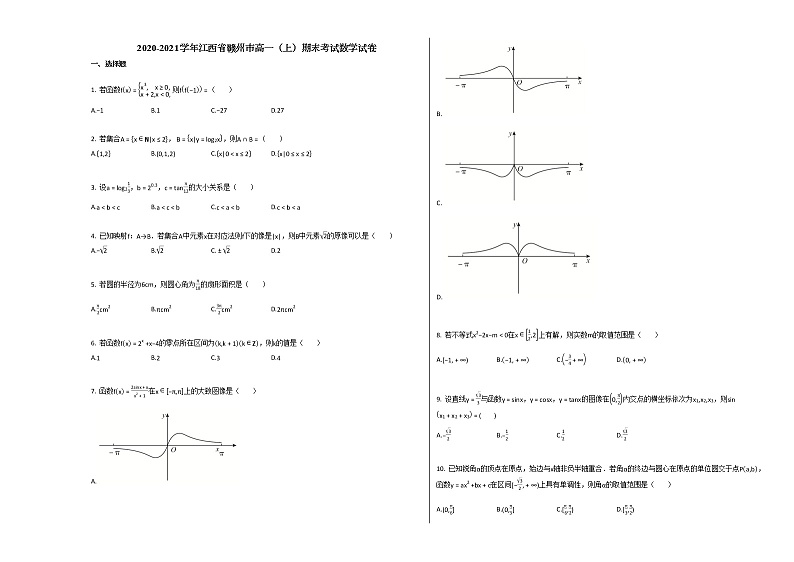
7. 函数fx=2sinx+xx2+1在x∈−π,π上的大致图像是( )
A.
B.
C.
D.
8. 若不等式x2−2x−m<0在x∈12,2上有解,则实数m的取值范围是( )
A.[−1,+∞)B.−1,+∞C.−34+∞D.0,+∞
9. 设直线y=33与函数y=sinx,y=csx,y=tanx的图像在0,π2内交点的横坐标依次为x1,x2,x3,则sinx1+x2+x3=( )
A.−32B.−12C.12D.32
10. 已知锐角α的顶点在原点,始边与x轴非负半轴重合.若角α的终边与圆心在原点的单位圆交于点Pa,b,函数y=ax2+bx+c在区间[−32,+∞)上具有单调性,则角α的取值范围是( )
A.(0,π6]B.(0,π3]C.[π6,π2)D.[π3,π2)
11. 已知m∈R,若函数fx=e|x+m|对任意x∈R满足f20x−21=f21−20x,则不等式flnx+fln1x≥2e的解集是( )
A.−∞,1e∪e,+∞B.1e,e
C.0,1e∪e,+∞D.[e,+∞)
12. 已知fx是定义在R上的奇函数, fx+1也是奇函数,当x∈(0,1]时,fx=1−1x.若函Fx=fx+sinπx,则Fx在区间1949,2021上的零点个数是( )
A.108B.109C.144D.145
二、填空题
满足{x, y}∪B={x, y, z}的集合B的个数是________.
若f2x=x2,则f8=________.
计算: 13lg8+lg50+120+338−23 =________.
下列判断正确的是________(将你认为所有正确的情况的代号填入横线上).
①函数y=1+tan2x1−tan2x的最小正周期为π;
②若函数f(x)=|lgx|,且f(a)=f(b),ab=1;
③若tan2α=3tan2β+2,则3sin2α−sin2β=2;
④若函数y=2x+12+sinx4x2+1的最大值为M,最小值为N,则M+N=2.
三、解答题
已知全集U=R,集合A=x|x2−2x≤0,B=x|x>1.
(1)求A∩∁RB;
(2)设集合C=x|x−ax−2≤0.若C∪A=A,求实数a的取值范围.
设函数fx=2cs2x−π3x∈R.
(1)在给定的平面直角坐标系中,用“五点法”画出函数fx在区间π6,7π6上的简图(请先列表,再描点连线);
(2)若fθ2=13,求sinθ+π6+2csθ+5π3的值.
设函数fx=x2+2x
(1)用定义证明函数fx在区间0,2上是减函数;
(2)若不等式fx≥ex−1−lg2m对任意x∈12,1恒成立,求实数m的最小值.
为减少人员聚集,某地上班族S中的成员仅以自驾或公交方式上班.分析显示,当S中有x%0
已知上班族S的人均上班时间计算公式为: gx=fx⋅x%+50100−x%,讨论gx的单调性,并说明实际意义.
(注:人均上班路上时间,是指单日内该群体中成员从居住地到工作地的平均用时.)
设函数fx=4sinωxcsωx−π6−1的最小正周期为π,其中ω>0.
(1)求函数fx的递增区间;
(2)若函数gx=fx+m在x∈π12,π2上有两个不同的零点x1,x2,求实数m的取值范围.
设函数f(x)=a2x−t+1ax(a>0且a≠1)是定义在R上的奇函数.
(1)若f1>0,求使不等式f2x2−x+fx2−k>0对x∈R恒成立的实数k的取值范围;
(2)设函数fx的图像过点1,32,函数gx=lgafx+1.若对于任意的x1,x2∈0,1,都有|gx1−gx2|≤M,求M的最小值.
参考答案与试题解析
2020-2021学年江西省赣州市高一(上)期末考试数学试卷
一、选择题
1.
【答案】
B
【考点】
函数的求值
分段函数的应用
【解析】
根据不同x的取值范围,然后代入求出不同的值.
【解答】
解:当x=−1时,x<0,
则f(−1)=x+2=−1+2=1.
当x=1时,x>0,
则f(1)=x3=13=1.
故选B.
2.
【答案】
A
【考点】
交集及其运算
【解析】
先化简集合A,B,再利用集合的运算求解即可.
【解答】
解:集合A=x∈N|x≤2=0,1,2,
B=x|y=lg2x=x|x>0,
∴ A∩B=1,2.
故选A.
3.
【答案】
B
【考点】
指数式、对数式的综合比较
正切函数的性质
【解析】
先求出a,b,c的范围,再来进行比较即可求解.
【解答】
解:∵ a=lg213
0
4.
【答案】
C
【考点】
映射
【解析】
利用集合A中元素x在对应法则f下的像是|x|,且|±2|=2,即可得到答案.
【解答】
解:映射f:A→B.
若集合A中元素x在对应法则f下的像是|x|,
且|±2|=2,
∴ B中元素2的原像可以是 ±2.
故选C.
5.
【答案】
B
【考点】
扇形面积公式
【解析】
利用扇形的面积公式S=12αr2进行求解即可.
【解答】
解:若圆的半径为r=6cm,
则圆心角为π18的扇形面积是12αr2=12×π18×62=πcm2.
故选B.
6.
【答案】
A
【考点】
函数零点的判定定理
【解析】
易知函数fx=2x+x−4在其定义域上连续且单调递增,从而利用零点的判定定理判断即可.
【解答】
解:易知函数fx=2x+x−4在其定义域上连续且单调递增,
且f1=2+1−4<0,
f2=22+2−4>0,
故f1f2<0
故函数fx=2x+x−4的零点在区间1,2上,
故k=1.
故选A.
7.
【答案】
A
【考点】
函数奇偶性的判断
函数奇偶性的性质与判断
函数图象的作法
【解析】
利用函数的奇偶性排除选项CD,利用特殊值排除B,即可得到答案.
【解答】
解:函数fx=2sinx+xx2+1,x∈−π,π,
∵ f−x=2sin−x+−x−x2+1=−2sinx+xx2+1=−fx,
∴ fx为奇函数,图象关于原点对称,故排除选项CD;
fπ2=2sinπ2+π2π22+1>0,故排除选项B.
故选A.
8.
【答案】
B
【考点】
二次函数的性质
【解析】
不等式x2−2x−m<0在x∈12,2上有解,则m>(x2−2x)min,设f(x)=x2−2x=(x−1)2−1,x∈12,2,求出f(x)min,即可得到答案.
【解答】
解:不等式x2−2x−m<0在x∈12,2上有解,
则m>(x2−2x)min,
设f(x)=x2−2x=(x−1)2−1,x∈12,2,
∴ 当x=1时,f(x)min=f(1)=1−2=−1,
∴ m>−1,
∴ 实数m的取值范围是(−1,+∞).
故选B.
9.
【答案】
D
【考点】
三角函数中的恒等变换应用
【解析】
本题考查三角函数恒等变换的运用.
【解答】
解:将y=33 分别代入得
sinx1=33,
csx2=33,
tanx3=33,
∵x∈0,π2,
∴csx1=1−sin2x1=63,
sinx2=1−cs2x2=63,
结合tanx3=sinx3csx3=33,
sin2x3+csx32=1,
得sinx3=12,csx3=32,
∴sin(x1+x2+x3)=sin[(x1+x2)+x3]
=sinx1+x2csx3+csx1+x2sinx3
=csx3(sinx1csx2+sinx2csx1)+sinx3(csx1csx2−sinx1sinx2)
=3233×33+63×63+1263×33−33×63
=3213+23
=32.
故选D.
10.
【答案】
D
【考点】
任意角的三角函数
正切函数的单调性
函数的单调性及单调区间
【解析】
利用二次函数的性质得到ba≥3,再利用任意角三角函数定义得到tanα=ba≥3,利用正切函数的性质求解即可.
【解答】
解:∵ 函数y=ax2+bx+c在区间[−32,+∞)上具有单调性,
∴ −b2a≤−32,
∴ ba≥3,
∴ tanα=ba≥3,
又∵ α为锐角,
∴ α∈[π3,π2).
故选D.
11.
【答案】
C
【考点】
奇偶性与单调性的综合
【解析】
由题意得到fx=e|x|为偶函数,且x≥0时,fx=ex单调递增,将不等式flnx+fln1x≥2e转化为f|lnx|≥f(1),进而得到|lnx|≥1,解不等式即可.
【解答】
解:函数fx=e|x+m|对任意x∈R满足f20x−21=f21−20x,
则函数fx=e|x+m|为偶函数,
∴ m=0,
∴ fx=e|x|,
∴ x≥0时,fx=ex单调递增,且f(1)=e,
不等式flnx+fln1x≥2e可转化为flnx+fln1x=flnx+f−lnx=2flnx≥2e,
∴ flnx≥e,
∴ f|lnx|≥f(1),
即|lnx|≥1,
解得 x∈0,1e∪e,+∞ .
故选C.
12.
【答案】
D
【考点】
函数奇偶性的性质
函数的零点
正弦函数的图象
【解析】
本题先由已知条件,认知当x∈−1,1时,
fx解析式和图象特征,然后依据函数
y=fx和y=−sinπx图象在前开后闭区间
(−1,1]上的交点个数,可推出函数
Fx=fx+sinπx在区间1949,2021上的交
点个数.
【解答】
解:∵fx是R上的奇函数,fx+1也是奇函数,
∴f−x=−fx,f1−x=−f1+x,f(0)=0,
即f1+x=−f1−x.
∴ f2+x=f1+1+x
=−f1−1+x=−f−x=fx,
可见fx是周期为2的周期函数.
又当0
∴ f(x)=1−1x,0,−1−1x,
函数Fx=fx+sinπx的零点个数,即方程fx=−sinπx的解的个数,即在同一坐标系中,函数y=fx与函数y=−sinπx图象交点的个数,画出草图,如图所示,
在区间长度为2的前闭后开的一个周期的区间[−1,1)上,两函数有4个交点,
.
而2021−1949=72=2×36,
∴函数Fx=fx+sinπx在闭区间1949,2021上,
共有4×36+1=145个零点.
故选D.
二、填空题
【答案】
4
【考点】
并集及其运算
子集与真子集
【解析】
根据{x, y}∪B={x, y, z},易知B⊆{x, y, z},且z∈B,用列举法写出满足已知条件的集合B,即可求出集合B的个数.
【解答】
解:∵ {x, y}∪B={x, y, z},
∴ B⊆{x, y, z},且z∈B,
∴ B={z},{x, z},{y, z},{x, y, z}.
故答案为:4.
【答案】
32
【考点】
函数的求值
【解析】
利用赋值法求解即可.
【解答】
解:f2x=x2,
令x=3,
可得f23=f(8)=32.
故答案为:32.
【答案】
319
【考点】
对数与对数运算
有理数指数幂的运算性质及化简求值
【解析】
利用对数的运算和指数幂的运算求解即可.
【解答】
解:13lg8+lg50+120+338−23
=13lg23+(lg5+lg10)+1+[323]−23
=lg2+lg5+1+1+(23)2
=lg(2×5)+1+1+49
=1+1+1+49
=319.
故答案为:319.
【答案】
③④
【考点】
命题的真假判断与应用
三角函数的周期性及其求法
分段函数的应用
函数奇偶性的性质与判断
对数及其运算
【解析】
利用函数的奇偶性的性质与判断、三角函数的周期性及求法、分段函数的应用.
【解答】
解:①y=1+tan2x1−tan2x=tanπ4+tan2x1−tanπ4tan2x=tan(π4+2x),
最小正周期T=π2,故①错误;
②f(x)=|lgx|,f(a)=|lga|,f(b)=|lgb|,
∵ f(a)=f(b),
∴ |lga|=|lgb|,
∴ lga=lgb或lga=−lgb=lg1b,
∴ a=b或ab=1.
故②错误;
③若tan2α=3tan2β+2,
则sin2αcs2α−3sin2βcs2β=2,
sin2α1−sin2α−3sin2β1−sin2β=2,
sin2α(1−sin2β)−3sin2β(1−sin2α)=2(1−sin2α)(1−sin2β),
化简得3sin2α−sin2β=2,故③正确;
④y=(2x+1)2+sinx4x2+1=4x2+4x+1+sinx4x2+1=1+4x+sinx4x2+1,
令ℎ(x)=4x+sinx4x2+1,ℎ(x)为奇函数,
设ℎ(x)max=ℎ(x0),则ℎ(x)min=ℎ(−x0),
∴ ymax=ℎ(x)max+1=ℎ(x0)+1=M,ymin=ℎ(x)min=ℎ(−x0)+1=N,
ymax+ymin得2+ℎ(x0)+ℎ(−x0)=M+N,可得M+N=2,故④正确.
综上,③④正确.
故答案为:③④.
三、解答题
【答案】
解:依题意,集合A=x|0≤x≤2.
(1)∵ ∁RB=x|x≤1,
∴ A∩∁RB=x|0≤x≤1.
(2)∵ C∪A=A,∴ C⊆A,
①当a>2时,C=x|2≤x≤a与C⊆A矛盾,故a>2不符合题意,
②当a≤2时,C=x|a≤x≤2,
若C⊆A,则a≤2a≥0,解得0≤a≤2,
由①②得,实数a的取值范围是0,2.
【考点】
集合的包含关系判断及应用
交、并、补集的混合运算
【解析】
暂无
暂无
【解答】
解:依题意,集合A=x|0≤x≤2.
(1)∵ ∁RB=x|x≤1,
∴ A∩∁RB=x|0≤x≤1.
(2)∵ C∪A=A,∴ C⊆A,
①当a>2时,C=x|2≤x≤a与C⊆A矛盾,故a>2不符合题意,
②当a≤2时,C=x|a≤x≤2,
若C⊆A,则a≤2a≥0,解得0≤a≤2,
由①②得,实数a的取值范围是0,2.
【答案】
解:(1)列表如下:
(2)由fθ2=2csθ−π3=13,
得csθ−π3=16.
由π6+θ+π3−θ=π2,
得sinθ+π6=csπ3−θ=csθ−π3=16,
由2π3+θ+π3−θ=π,
得cs(θ+5π3)=cs(θ+2π3+π)=−cs(θ+2π3)=cs(π3−θ)=16,
则sinθ+π6+2csθ+5π3=3csπ3−θ=12.
【考点】
五点法作函数y=Asin(ωx+φ)的图象
三角函数中的恒等变换应用
诱导公式
【解析】
暂无
暂无
【解答】
解:(1)列表如下:
(2)由fθ2=2csθ−π3=13,
得csθ−π3=16.
由π6+θ+π3−θ=π2,
得sinθ+π6=csπ3−θ=csθ−π3=16,
由2π3+θ+π3−θ=π,
得cs(θ+5π3)=cs(θ+2π3+π)=−cs(θ+2π3)=cs(π3−θ)=16,
则sinθ+π6+2csθ+5π3=3csπ3−θ=12.
【答案】
(1)证明:任取x1,x2∈0,2,且x1
∵x1,x2∈0,2,且x1
∴ fx在0,2上是减函数,证毕.
(2)解:∵ 不等式fx≥ex−1−lg2m对任意x∈12,1恒成立,
∴ lg2m≥ex−1−x+2x对任意x∈12,1恒成立.
令gx=ex−1−x+2x,
结合(1)知,gx在x∈12,1上单调递增,
则gxmax=g1=−2.
则lg2m≥−2,即lg2m≥lg22−2=lg214,
解得m≥14.
【考点】
函数单调性的判断与证明
函数单调性的性质
函数恒成立问题
【解析】
暂无
暂无
【解答】
(1)证明:任取x1,x2∈0,2,且x1
∵x1,x2∈0,2,且x1
∴ fx在0,2上是减函数,证毕.
(2)解:∵ 不等式fx≥ex−1−lg2m对任意x∈12,1恒成立,
∴ lg2m≥ex−1−x+2x对任意x∈12,1恒成立.
令gx=ex−1−x+2x,
结合(1)知,gx在x∈12,1上单调递增,
则gxmax=g1=−2.
则lg2m≥−2,即lg2m≥lg22−2=lg214,
解得m≥14.
【答案】
解:(1)依题意,得①当0
30
即当x=20或x=45时自驾群体的人均上班时间等于公交群体的人均上班时间.
(2)①当0
∴ 当x∈0,35时gx单调递减,当x∈35,100时gx单调递增.
说明该地上班族S中有小于35%的人自驾时,人均上班时间递减;当大于35%的人自驾时,人均上班时间递增;当自驾人数等于35%时,人均上班时间最少.
【考点】
函数模型的选择与应用
分段函数的应用
根据实际问题选择函数类型
函数的单调性及单调区间
【解析】
暂无
暂无
【解答】
解:(1)依题意,得①当0
30
即当x=20或x=45时自驾群体的人均上班时间等于公交群体的人均上班时间.
(2)①当0
∴ 当x∈0,35时gx单调递减,当x∈35,100时gx单调递增.
说明该地上班族S中有小于35%的人自驾时,人均上班时间递减;当大于35%的人自驾时,人均上班时间递增;当自驾人数等于35%时,人均上班时间最少.
【答案】
解:(1)依题意,fx=3sin2ωx−cs2ωx=2sin2ωx−π6.
∵fx的最小正周期为π,且ω>0,
∴ 2π2ω=π,解得ω=1,
∴ fx=2sin2x−π6.
设u=2x−π6,
∵ 函数y=sinu的递增区间是2kπ−π2,2kπ+π2k∈Z,
由2kπ−π2≤2x−π6≤2kπ+π2k∈Z,
得kπ−π6≤x≤kπ+π3k∈Z.
∴ 函数fx的递增区间是kπ−π6,kπ+π3k∈Z.
(2)当x∈π12,π2时,u=2x−π6∈0,5π6.
令Fu=2sinu,则Fπ6=F5π6=1.
∵Fu=2sinu在u∈0,π2上递增,在u∈π2,5π6上递减,
∴ Fumax=Fπ2=2.
∵ 函数gx=fx+m在x∈π12,π2上有两个不同的零点,
∴ 函数y=fx与y=−m两图像在x∈π12,π2上有两个不同的交点,
∴ 函数y=Fu与y=−m两图像在u∈0,5π6上有两个不同的交点,
∴ 1≤−m<2,解得−2
【考点】
y=Asin(ωx+φ)中参数的物理意义
函数解析式的求解及常用方法
正弦函数的单调性
函数的零点与方程根的关系
函数的零点
【解析】
暂无
暂无
【解答】
解:(1)依题意,fx=3sin2ωx−cs2ωx=2sin2ωx−π6.
∵fx的最小正周期为π,且ω>0,
∴ 2π2ω=π,解得ω=1,
∴ fx=2sin2x−π6.
设u=2x−π6,
∵ 函数y=sinu的递增区间是2kπ−π2,2kπ+π2k∈Z,
由2kπ−π2≤2x−π6≤2kπ+π2k∈Z,
得kπ−π6≤x≤kπ+π3k∈Z.
∴ 函数fx的递增区间是kπ−π6,kπ+π3k∈Z.
(2)当x∈π12,π2时,u=2x−π6∈0,5π6.
令Fu=2sinu,则Fπ6=F5π6=1.
∵Fu=2sinu在u∈0,π2上递增,在u∈π2,5π6上递减,
∴ Fumax=Fπ2=2.
∵ 函数gx=fx+m在x∈π12,π2上有两个不同的零点,
∴ 函数y=fx与y=−m两图像在x∈π12,π2上有两个不同的交点,
∴ 函数y=Fu与y=−m两图像在u∈0,5π6上有两个不同的交点,
∴ 1≤−m<2,解得−2
【答案】
解:(1)∵fx是定义在R上的奇函数,
∴f0=0,∴2−t=0,解得t=2,
则fx=a2x−1ax ,
而f2x2−x+fx2−k>0等价于f2x2−x>−fx2−k=fk−x2,
若f1>0,则a2−1a>0,结合a>0且a≠1,解得a>1,
则f(x)=a2x−1ax=ax−1ax(a>1)为增函数,
结合f2x2−x>fk−x2,可得2x2−x>k−x2,
根据题意,3x2−x−k>0对x∈R恒成立.
则Δ=1+12k<0,解得k<−112.
(2) ∵函数fx的图像过点[ 132),
∴f1=a2−1a=32,
解得a=−12(舍去)或a=2,
∴gx=lg22x−12x+1,
根据复合函数“同增异减”可知gx[x∈0,1上单调递增,
∵对于任意的x1,x2∈0,1,都有|gx1−gx2|≤M,
解得a=−1(不符,舍去)或a=2,
∴gx=lg22x−12x+1,
根据复合函数“同增异减”可知gx在x∈0,1上单调递增,
∵对于任意的x1,x2∈0,1,都有|gx1−gx2|≤M,
且gx在区间0,1上恒有gx>0,
∴M≥gxmax−gxmin,
则gxmin=g0=0,gxmax=g1=lg252,
则M≥lg252−0=lg252,
即M的最小值为lg252.
【考点】
函数奇偶性的性质
奇偶性与单调性的综合
函数恒成立问题
函数的求值
【解析】
无
无
【解答】
解:(1)∵fx是定义在R上的奇函数,
∴f0=0,∴2−t=0,解得t=2,
则fx=a2x−1ax ,
而f2x2−x+fx2−k>0等价于f2x2−x>−fx2−k=fk−x2,
若f1>0,则a2−1a>0,结合a>0且a≠1,解得a>1,
则f(x)=a2x−1ax=ax−1ax(a>1)为增函数,
结合f2x2−x>fk−x2,可得2x2−x>k−x2,
根据题意,3x2−x−k>0对x∈R恒成立.
则Δ=1+12k<0,解得k<−112.
(2) ∵函数fx的图像过点[ 132),
∴f1=a2−1a=32,
解得a=−12(舍去)或a=2,
∴gx=lg22x−12x+1,
根据复合函数“同增异减”可知gx[x∈0,1上单调递增,
∵对于任意的x1,x2∈0,1,都有|gx1−gx2|≤M,
解得a=−1(不符,舍去)或a=2,
∴gx=lg22x−12x+1,
根据复合函数“同增异减”可知gx在x∈0,1上单调递增,
∵对于任意的x1,x2∈0,1,都有|gx1−gx2|≤M,
且gx在区间0,1上恒有gx>0,
∴M≥gxmax−gxmin,
则gxmin=g0=0,gxmax=g1=lg252,
则M≥lg252−0=lg252,
即M的最小值为lg252.x
π6
5π12
2π3
11π12
7π6
2x−π3
0
π2
π
2π3
2π
2cs2x−π3
2
0
−2
0
2
x
π6
5π12
2π3
11π12
7π6
2x−π3
0
π2
π
2π3
2π
2cs2x−π3
2
0
−2
0
2
2020-2021学年江西省赣州市高三(上)期末考试数学(文)试卷北师大版: 这是一份2020-2021学年江西省赣州市高三(上)期末考试数学(文)试卷北师大版,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年江西省赣州市高三(上)期末考试数学(理)试卷北师大版: 这是一份2020-2021学年江西省赣州市高三(上)期末考试数学(理)试卷北师大版,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年江西省赣州市高二(上)12月月考数学试卷北师大版: 这是一份2020-2021学年江西省赣州市高二(上)12月月考数学试卷北师大版,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












